どーんとこい!中学入試の算数
第1回 つるかめ算
2017.1.26
12.5K



大人でもちょっと手こずってしまうような、難問奇問が続出する中学入試の算数。
でもだいじょうぶ、コツさえつかめば怖くありません!
学習サポートセンターのカズが、算数を楽しく学ぶ方法を伝授します。
こんにちは。学習アドバイザーのカズです。2017年度もこのコーナーを担当することになりました。
おもしろい わかりやすくて ためになる
そんなコーナーを目指して、本年もがんばります。乞うご期待ください。
では、早速始めましょう。初回は
特殊算って、なーに?
です。特殊算というと、何か難しい計算のようにも感じてしまいますが、言ってしまえば、中学校で学ぶ方程式を「小学生でも解けるように開発した特別な計算方法」です。中学校に入って学ぶ方程式を使えば解ける問題であるため、中学受験をしないかぎり勉強しない内容です。
では、なぜ一般的には学習しない内容を、中学受験では勉強しなければならないのか。それは、入試を行う中学校にとって、思考力を測るのに格好の題材だからです。今回は、特殊算のなかでも代表的な「つるかめ算」に挑戦してみましょう。
問題
さぽナビ水族館の巨大水そうの中には、イカとタコとヒトデがいます。このとき、次の各問いに答えましょう。
(1)つぼの中や岩かげなどに隠れているイカとタコが合わせて18匹います。足の数が合わせて158本あるとき、イカとタコはそれぞれ何匹ずついるでしょう。
(2)姿の見えているイカとタコとヒトデは、合わせて16匹います。足の数が合わせて108本で、ヒトデがイカの4倍いるとき、イカとタコとヒトデはそれぞれ何匹ずついるでしょう。
ここでは、足の数はイカは10本、タコは8本、ヒトデは5本で考えてみてください。

|
(ヒント) つるかめ算ならぬイカタコ算ですね。 (1)タコが18匹だったら、足の数はどれだけ足りないでしょう。また、17匹、16匹と数を減らしていくと、足の本数はどのように変化するでしょう。表などを作って考えてみてください。 (2)イカとヒトデの足の数が、ともに5の倍数になっていることに着目します。108本からタコの足の数を引くと、5の倍数になりますので、タコの数から考えていくようにしましょう。なお、求めるものが3種類のつるかめ算を「つるかめカブトムシ算」といいます。その場合、足の数が2本、4本、6本で出題されるということですね。 (参考) |
今回の記事では、わかりやすくイカ・タコ・ヒトデの「足」と表現しましたが、実はわたしたちが足だと思っているものは「腕(わん)」ともいうそうです。生態を調べてみると、ほかにも意外な事実が発覚しました。興味のある方は、ぜひ調べてみてくださいね。
それでは、今回の解答解説を確認してみましょう。
解答・解説はこちら
(1)イカとタコを合わせた数が18匹ですから、表を作ってみましょう。
| イカ | 0 | 1 | 2 | … | 16 | 17 | 18 |
| タコ | 18 | 17 | 16 | … | 2 | 1 | 0 |
| 足の合計 | 144 | 146 | 148 | … | 176 | 178 | 180 |
イカが0匹のとき、足の合計は144本です。そこからイカが1匹増えるごとに、足の合計が2本ずつ増えていくのがわかりますよね。この増えていく2本は、イカとタコの足の数の差です。
足の合計は158本ですから、
(158-144)÷2=7
つまり、イカが7匹、タコが11匹のときに足の数が158本になることがわかります。 (答)
ちなみに、イカを18匹として考える計算方法は
(18×10-158)÷(10-8)=11
で、タコが11匹と求めることができます。
(2)足の合計は108本で、これは5で割ると3あまる数です。
イカとヒトデの足の数が5の倍数なので、タコの合計の足の数は108から5の倍数を引いた数になり、これも5で割ると3あまる数になります。
そのような数は8、48、88で、そのときタコは1匹、6匹、11匹となります。
したがって、タコとヒトデとイカを合わせた数が16匹で、ヒトデがイカの4倍であることから
・タコが1匹のとき
イカが3匹、ヒトデが12匹。でも、足の数が98本。
・タコが6匹のとき
イカが2匹、ヒトデが8匹。このとき、足の数が108本。
・タコが11匹のとき
イカが1匹、ヒトデが4匹。でも、足の数が118本。
よって、求める答えは
イカが2匹、タコが6匹、ヒトデが8匹(答)
となります。
別解
実は、中学受験の算数では、面積図を用いて解くこともできます。面積図の勉強をされている方は、下図を参考に考えてみてください。
(1)縦の長さは足の数、横の長さは個体の数で面積図を書きます。
斜線部分の横の長さから、イカの数を求めてみましょう。
(2)
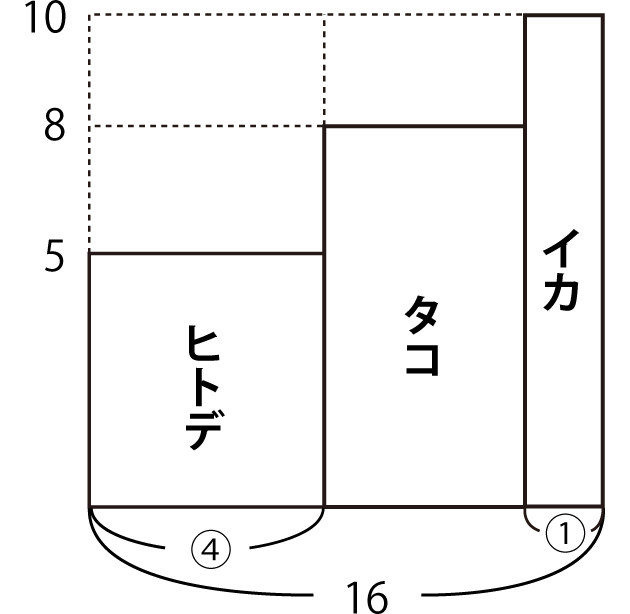
縦の長さは足の数、横の長さは個体の数で面積図をかきます。ヒトデはイカの4倍です。
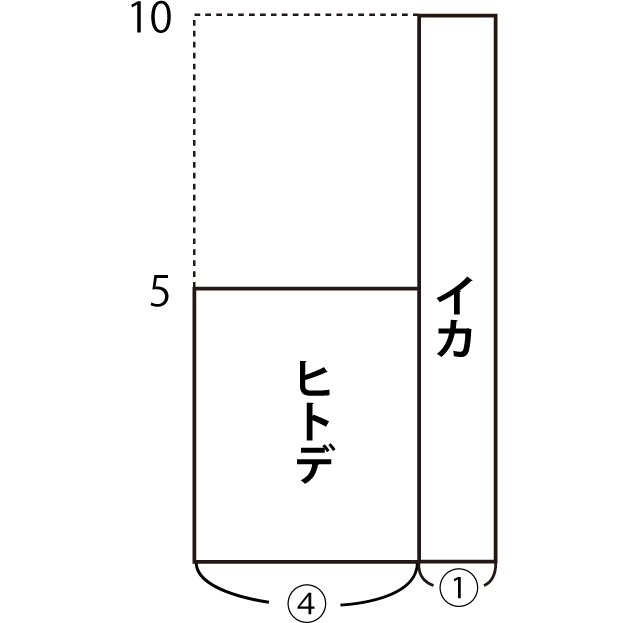

次に、個体数のわかっているヒトデとイカをひとつの長方形にまとめます。
ヒトデとイカの個体数の比は4:1なので、全体を5と考えると、
平均の足の数は以下のように求められます。
(5×4+10×1)÷5=6
よって、ヒトデとイカをひとつの長方形にまとめた長方形の高さは6となります。


あとは(1)の面積図と同じように、斜線部分の横の長さから、タコの数を求めましょう。
いかがでしたでしょうか。ヒントもつけましたし、生まれたての「オタマジャクシ」ってことはないですよね。
?????
いやいや、手も足も出ないということです。これからもみなさんが
解いて、読んで、納得する
記事を目指しますので、本年度もどうぞよろしくお願いいたします。
プロフィール
出題・文
学習サポートセンター カズ
Z会の学習サポートセンターで、日夜会員のみなさんからの質問相談に応じている。















