どーんとこい!中学入試の算数
第21回 視野を広げて考えてみる
2018.9.27
4.6K



大人でもちょっと手こずってしまうような、難問奇問が続出する中学入試の算数。
でもだいじょうぶ、コツさえつかめば怖くありません!
学習サポートセンターのカズが、算数を楽しく学ぶ方法を伝授します。
こんにちは。学習アドバイザーのカズです。今回は面積を求める問題を通して、視野を広げて考えることの大切さを実感していただきます。日常生活でも、部分最適に陥り全体としてよくなかったなんてことがよくあるのではないでしょうか。
世の中を見てみても、一部の人にとってはよいことかもしれないけれど、全体としては不利益を被るということも少なくありません。そこで、全体の利益を最大にするという考え方が必要になってくるのです。
たとえば、多くの人が楽しみにしているオリンピックですが、開催には巨額の経費がかかります。また、めぐまれない子どもたちを何とかしてあげるための福祉にもお金が必要です。限られたお金をどのように配分するのがよいのか。当事者や関係者の方々にはそれぞれに考えや言い分があると思いますが、お金は無尽蔵にあるわけではないので、全体を見て最適と思われる配分をする必要があるわけです。得てしてお金持ちや権力のある人に都合よく配分の仕方が決まり、格差が拡大してしまうこともありますが、それを続けていくのは社会全体にとって不利益なのです。
では、すべての問題を解決し、人々の生活をよくするためには、どうしたらよいのか。一つ言えるのは、俯瞰的・大局的にものを見、考えることによって、価値の創造や社会の変革をもたらすことが不可欠だということです。
子どもたちはこれから、どんな選択をしてどう生きていくべきなのか。自分の利益ばかり追うのではなく、社会全体がよりよい方向に進んでいくような選択ができるとよいですね。この記事が、そんなことを考えるきっかけになればうれしいです。
問題
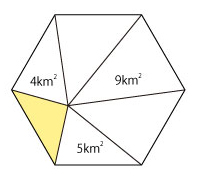
南の島に、正六角形の形をした埋立地があります。ゴミを埋め立てて作った島のため、このたび格安で売りに出すことにしました。
右図のように、3つの三角形については面積がわかっています。1km2が税込み100万円であるとき、黄色い部分の土地はいくらで買えるでしょう。
|
ヒント 正六角形の中だけで考えたのでは難しいでしょう。ここは、視野を広げて(?)正三角形を作って考えてみましょう。 (参考) 2018年度灘中学校 1日目第10問 2018年度東大寺学園 第1問(2) |
ちまたでは、「君たちはどう生きるか(吉野源三郎著)」が話題になっていますね。この本がヒットするずっと前に、2011年度の千葉中学校の入試問題(適性検査)でも取り上げられたことがあります。
受験に合格することも大切ですが、これからをどう生きるのか。お子様といっしょにいろいろと話ができるといいですね。
解答・解説はこちら
解答
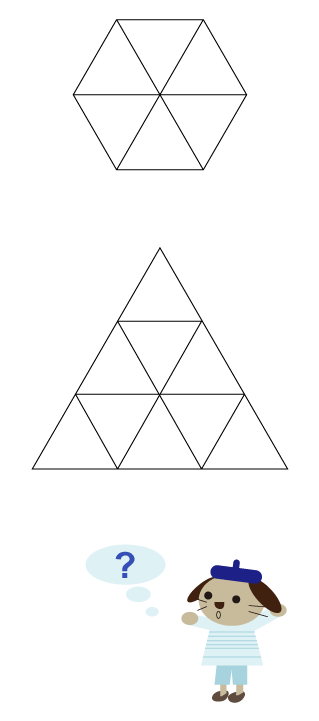
右図のように、正六角形は小さい三角形6個分です。
したがって、小さい正三角形9個で大きな正三角形を作り、
まずはこの大きな正三角形の面積を求めます。
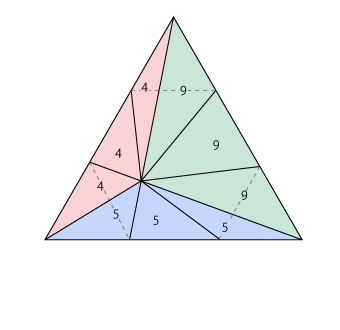
底辺、高さの等しい三角形の面積は同じですから、小さい正三角形9個分の大きな三角形の面積は
(4+5+9)×3=54(km2)
小さい正三角形1個分は、54÷9から6km2となります。
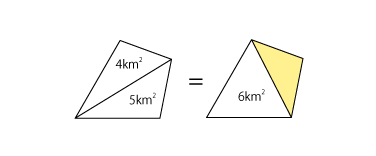
よって、求める面積は
(4+5)-6=3(km2)
すなわち、300万円であることがわかります。 (答)
いかがでしたでしょうか。この問題では、正六角形を含む大きな正三角形の中で考えることがポイントでした。参考にした灘中学校の問題だけでなく、東大寺学園の問題も同様の解き方で解くことができます。余力のある方は、2校の過去問題にも挑戦してみてください。
この問題を通して、「視野を広げて考えてみる」って大切なんだな。そう思っていただけたなら、出題者としてうれしい限りです。
それでは、また来月にお会いしましょう。
プロフィール
出題・文
学習サポートセンター カズ
Z会の学習サポートセンターで、日夜会員のみなさんからの質問相談に応じている。















