どーんとこい!中学入試の算数
第27回 渋幕でも出題された! 図形のあるある問題
2019.3.28
9.2K



大人でもちょっと手こずってしまうような、難問奇問が続出する中学入試の算数。
でもだいじょうぶ、コツさえつかめば怖くありません!
学習サポートセンターのカズが、算数を楽しく学ぶ方法を伝授します。
「ウカルンダーZからの挑戦状」の結果報告
中学受験コース5年生3月号の受講者を対象に、難関校でもよく出題される整数問題を出題した「ウカルンダーZからの挑戦状」を配信し、3月8日(金)~3月10日(日)の期間で、会員の皆さまの解答を募集しておりました。ハイレベルな問題に一生懸命取り組んだ様子がうかがえました。
本企画は、保護者の皆さまに向けて、さぽナビで結果のご報告記事を更新しています。
「解答解説編」では、応募された解答のなかから、いいところに目をつけられていた会員やポイントをしっかりおさえられていた会員の答案紹介も行っております。
4年生や6年生の保護者の皆さまも、ぜひご覧ください。
※すでに、解答の募集は終了しておりますので、ご了承ください。
こんにちは。学習アドバイザーのカズです。今回は、よくある問題なんだけど、知らなければ超難問。知っていればすぐに解ける。そんな問題を出題します。
例年、いろいろとかたちを変えて出題されていますが元ネタはいっしょ。Z会の中学受験コースでは、3年生12月号の算数アトラクションで扱っています。また10年以上前には、SEGという塾の広告宣伝にも使われていた問題です。
少し手を入れて、面積の問題も加えて出題していますので、元ネタを知っている方でも十分に楽しめる内容ではないかと思います。初見の場合には結構考えさせられますが、難関中学校の先生方はおもしろい問題だと思って出題しているのだと思いますので、ひとつの経験と思ってチャレンジしてみてください。
さっそくですが、問題を見ていきましょう。
問題
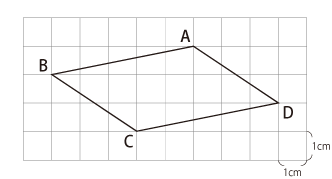
右の平行四辺形について、次の問いに答えなさい。ただし、マス目の目盛りは1cm、円周率を3.14とします。
(1)平行四辺形ABCDの面積を求めなさい。
(2)角BADの角度を求めなさい。
(3)3点A、C、Dを通る円の面積を求めなさい。
|
ヒント (1)は問題ないでしょう。 (2)が主題であり、参考入試問題にも出題されているものです。3年生の教材がある方は、12月号の算数アトラクションを見てみるとよいでしょう。角BAD の角度を求める問題ですが、角ABCを求めて180度からひくことで求めることができます。 (3)も難関校ではよく見られる問題です。半径の長さを求めることはできません。こちらも4年生1月号の算数アトラクションを読むと、理解が深まります。お手元にある場合には、ぜひどうぞ。 (参考) 2019年度渋谷教育学園幕張中学校 第4問(2) 2018年度筑波大学附属中学校 第1問(7) |
次回以降も、2019年度に出題されたおもしろいと思った問題を題材に出題していく予定です。
解答・解説はこちら
解答
(1)
平行四辺形ABCDを図1のように分けると、長方形と4つの直角三角形をあわせたものだから
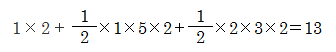
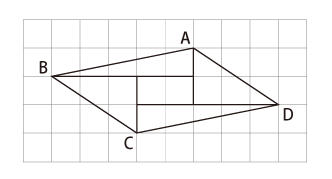
したがって、平行四辺形ABCDの面積は
13(cm2) (答)
(2)
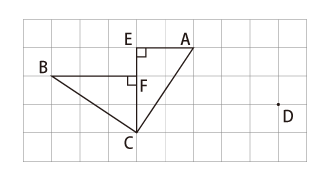
2点E、Fを図2のようにとると、三角形CFBと三角形AECは直角をはさむ2辺が2cmと3cmの合同な直角三角形になる。このとき、角BCFと角ECAをあわせた角度は、角BCFと角FBCをあわせた角度に等しいので、
角BCF+角FBC=180度-90度=90度
さらに、BC=CAだから、三角形ABCは直角二等辺三角形である。すなわち
角ABC=45度
したがって、角BADは
135度 (答)
(3)
(2)より三角形ABCは直角二等辺三角形であり、同様にして三角形ACDも直角二等辺三角形である。よって、辺CDは3点A、C、Dを通る円の直径に等しく、三角形ABCを図3のように移すと四角形ACGDは円の内側で接する正方形になる。
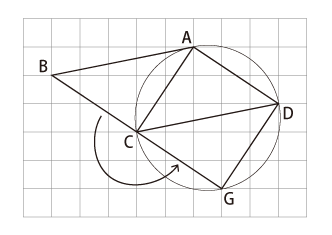
(1)より正方形ACGDの面積は13cm2であり、これは半径×半径の2倍だから、求める円の面積は
13÷2×3.14=20.41(cm2) (答)
いかがでしたでしょうか。初見だと少し難しい問題ですが、知っておくと武器になります。ポイントは
- 角度を求める「あわせる」問題は、直角二等辺三角形を作る。
- 円の面積を求める問題で「半径がわからない」問題は、「半径×半径」を他のものに置き換える。
こういったことを念頭において考えるとよいでしょう。2019年度は、今後
- それぞれの面積は求められないけれども、あわせた面積は求められる。
そんな問題も紹介していきたいと考えています。それでは、次回もお楽しみに!
まだZ会員ではない方
プロフィール
出題・文
学習サポートセンター カズ
Z会の学習サポートセンターで、日夜会員のみなさんからの質問相談に応じている。
















