どーんとこい!中学入試の算数
第29回 灘中学校の算数入試問題のヒミツ!
2019.5.23
28.8K



大人でもちょっと手こずってしまうような、難問奇問が続出する中学入試の算数。
でもだいじょうぶ、コツさえつかめば怖くありません!
学習サポートセンターのカズが、算数を楽しく学ぶ方法を伝授します。
灘中学校の算数入試は、算数マニアの間では有名かもしれません。筑駒、開成と比べても格別なものがあります。解いていてわくわくするし、おもしろいと感じる問題が多いのです。そんな問題はどうやって生まれているのか。そのヒミツの一端に触れたような気がするできごとがありました。それはカズが20代のときに遡ります。
カズは20代のときに、灘中・高で数学を教える、ある先生と文通をしていました。数学専門誌がきっかけだったのですが、とても数学愛にあふれた方だと感じたのを覚えています。年賀状には小さい字で数学の問題が3題ほど書いてあり、そのどれもがよく練られた、すばらしい問題でした。そして「灘の生徒だからこそ、授業が成立する」とコメントが書かれていたのを思い出します(後に、その先生は数学者・京都大学の名誉教授である佐藤雅彦先生を教えていたことがあったと知りました)。
その先生は、数学が好きで、常に問題を考え続け、解く人のことを一生懸命に考えて問題を作っていました。きっと、灘中の入試問題を作ることもあったでしょう。これだけ数学を愛している先生が作る入試問題ですから、仕事の一貫として義務的に作られた問題ではなく、探究心の延長上でできた問題だったのではないでしょうか。そして、この先生に限らず、灘中・高の数学の先生は探究心が旺盛な方ばかりなのではないかなと推測します。だからこそ、毎年すばらしい入試問題が作られ続けているのでしょう。
今回は、そんな灘中学校の入試問題を題材にします。
問題
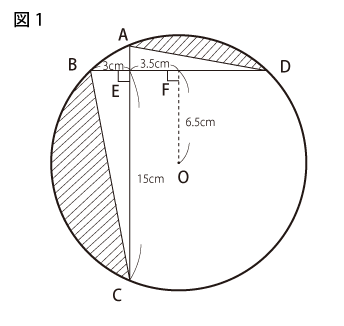
図1のような点Oを中心とする円について、次の問いに答えなさい。ただし、円周率は3.14とします。
(1)角BADの大きさを求めなさい。
(2)斜線部分の面積の和を求めなさい。
|
ヒント (1)こちらは4月号の復習です。第27回の出題を参考にしてみてください。 (2)円の面積についても、第27回の出題を参考にしてください。半径を求めることはできません。 (参考) 2019年度灘中学校1日目 第8問 2019年度渋谷教育学園幕張中学校 第4問(2) |
解答・解説はこちら
解答
(1)
ACとOFは平行だから、AE+OFはAE+ECの半分です。したがって
(AE+OF)×2=AE+EC
から
AE=EC-OF×2=15-6.5×2=2
ここで
ED=BF×2-BE=6.5×2-3=10
また、角BADは180°から角ABEと角ADEをひいた角です。
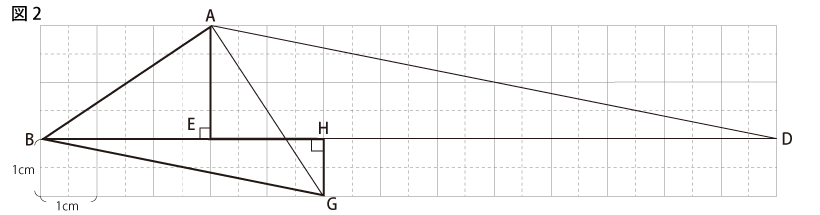
よって、図2のようにG、Hをとると、三角形ABGは直角二等辺三角形であり、三角形AEDと三角形GHBは相似だから、角ABEと角ADEを合わせた角度は45°です。
すなわち、角BADは
180°-45°=135° (答)
(2)
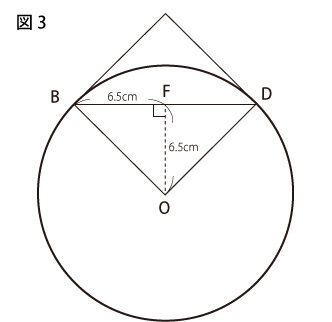
図3から、三角形FBOは直角二等辺三角形です。この直角三角形が4つ集まった正方形の面積は
6.5×6.5×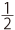 ×4=6.5×6.5×2
×4=6.5×6.5×2
となり、正方形の面積は1辺×1辺なので、円の面積を求めるために必要な「半径×半径」が6.5×6.5×2ということがわかります。
よって、この円の面積は、
6.5×6.5×2×3.14
=13×13×1.57
=169×1.57
=265.33(cm2)
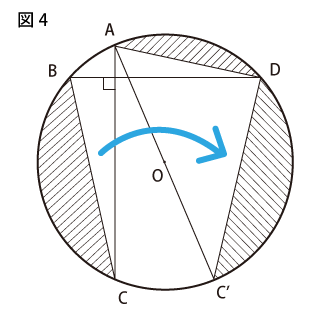
次に、図4のように左下の斜線部分を、直線OFを線対称の軸として移します。Cの移った先をC´とすると、C´はAOの延長上にあるので、AC´は円の直径になり、求める面積は半円から三角形AC´Dをひけばよいことがわかります。したがって、AC、BDに平行な直線で三角形AC´Dを囲んだ図5から、求めると
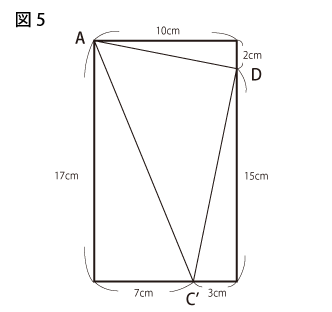
三角形AC´Dの面積は
17×10-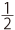 ×(17×7+10×2+15×3)=170-92=78
×(17×7+10×2+15×3)=170-92=78
よって、求める斜線部分の面積の和は
265.33×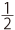 -78=54.665(cm2) (答)
-78=54.665(cm2) (答)
(別解)
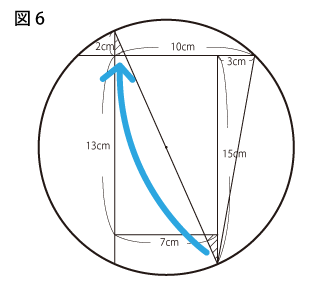
実は、図6より
265.33-13×7=174.33
の半分から直角三角形を2個ひくことで求めることもできます。
174.33÷2-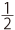 ×(2×10+15×3)
×(2×10+15×3)
=54.665(cm2)
こうして見てみると、本問も基本事項の組み合わせで解けることがわかります。でも、かなり難しいですね。
今回は以上でおしまい。それでは、また来月にお会いしましょう。
まだZ会員ではない方
プロフィール
出題・文
学習サポートセンター カズ
Z会の学習サポートセンターで、日夜会員のみなさんからの質問相談に応じている。
















