どーんとこい!中学入試の算数
第31回 点と点をつなぐ図形の問題
2019.7.25
5.4K



大人でもちょっと手こずってしまうような、難問奇問が続出する中学入試の算数。
でもだいじょうぶ、コツさえつかめば怖くありません!
学習サポートセンターのカズが、算数を楽しく学ぶ方法を伝授します。
【中学受験コース5年生の皆さまへ!】7月26日(金)に、「ウカルンダーZからの挑戦状」を配信します!
7月26日(金)に、中学受験コース5年生8月号をご受講の方を対象に「Z会小学生学習アプリ」の「情報ひろば」に「ウカルンダーZからの挑戦状」を配信します。ハイレベルな算数の問題が1問出題されますので、ぜひ挑戦するよう、お子さまにお声がけください。
今回の「ウカルンダーZからの挑戦状」では、数の規則性の問題を出題します。根気よく考え、そこから「ある法則」に気がつけるかどうかが、今回の出題のポイントです。難関校の入試でも数の規則性の問題は頻出ですので、ぜひ挑戦してみてください。
問題が解けたら、ぜひお子さまの考え方・解き方と答えを写真に撮って、7月28日(日)までに「情報ひろば」の専用フォームから応募してください。届いた答案のすべてに当コーナーの出題者カズが目を通します。よく書けている会員の考え方は、8月8日(木)に「情報ひろば」に配信する解答解説編でご紹介します。
こんにちは。学習アドバイザーのカズです。
今年度の海陽中等教育学校の入試問題を見たとき、なつかしさが込み上げてきました。なぜかというと、昔、カズがテレビのクイズ番組の「問題募集」に投稿した問題と同じものが出ていたからです。
それは1990年のこと。板東英二さんが司会を務める番組「マジカル頭脳パワー」です。カズの投稿した問題はあえなくボツになったのですが、今回は、そんな思い出をなつかしみながらの出題です。
問題
異なる4つの点を結んでできる6本の線について、長さが2種類になるものを考えます。たとえば、次の図は長い線2本と短い線4本からできる図形です。
このような条件をみたす図形で、次の図以外のものをすべてあげなさい。

|
ヒント (ヒント) |
解答・解説はこちら
解答
ヒントに書いたように、正四面体をつぶしてできた平面図形をイメージすると、漏れなく条件をみたす図形をあぶり出すことができます。長い辺を長辺、短い辺を短辺と呼ぶことにします。
【長辺1、短辺5の形】
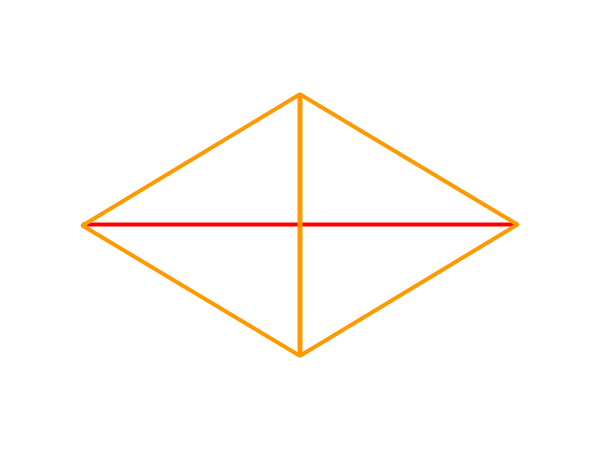
上の図形が該当します。
【長辺5、短辺1の形】
正四面体において、ひとつの辺だけを短くしていきます。すると、2点が重なってしまうので、条件をみたしません。
【長辺2、短辺4の形】
この場合は、長辺の2辺が1点を共有する場合と共有しない場合に分けます。
- 長辺の2辺が1点を共有する場合

上の図形が該当します。
- 長辺の2辺が1点を共有しない場合
問題文の図形が該当します。
【長辺4、短辺2の形】
この場合も、短辺の2辺が1点を共有する場合と共有しない場合に分けます。
- 短辺の2辺が1点を共有する場合
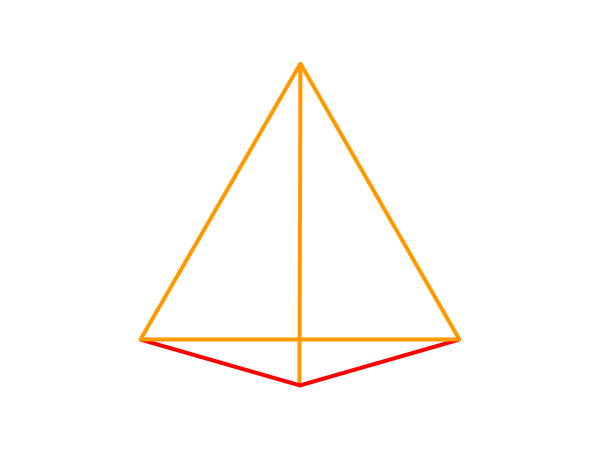
上の図形が該当します。
- 短辺の2辺が1点を共有しない場合
正四面体において、二つの辺を短くしていきます。すると、2点ずつ2か所で重なってしまうので、条件をみたしません。
【長辺3、短辺3の形】
この場合も、長辺(または短辺)の3辺が1点を共有する場合と、3辺がつながっている場合に分けます。
- 長辺(短辺)の3辺が1点を共有する場合
正四面体において、3本の辺を長くしていきます。すると、どこまでも長くなり条件をみたしません。
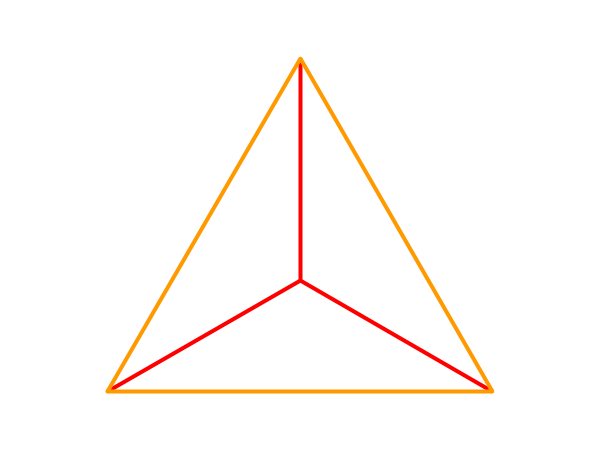
3本の辺を短くすると、上の図形が該当します。
- 長辺の3辺が1点を共有せず、つながっている場合
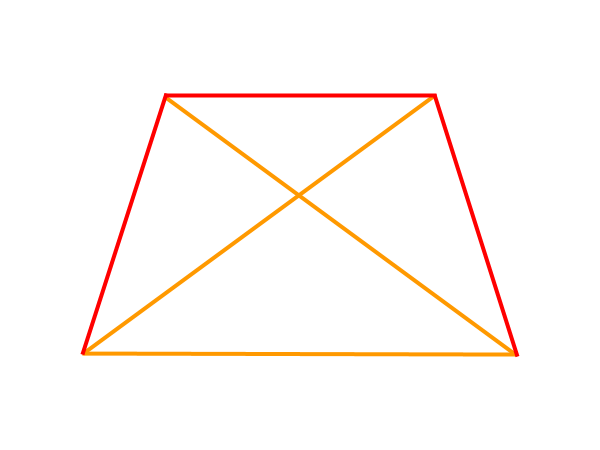
上の図形が該当します。つながっている長辺の両端を交差するように、平面上に移すことがポイントになります。
以上のように考えていくと、6種類以外にはないことがわかります。問題文に出てきた以外の5種類が答えになります。
(答)
カズが昔投稿した問題は、5種類の図形を見せておいて、残りの1種類を答えさせる問題でした。等脚台形が気づきにくいと考え、それを答えにしたのですが、何も連絡がなく悔しい思いをしました。
なお、海陽中等教育学校の実際の入試では、残り5つのうちから3つを図示する問題でした。興味のある方は、問題を見てみてくださいね。
今回は以上でおしまい。それでは、また来月にお会いしましょう。
まだZ会員ではない方
プロフィール
出題・文
学習サポートセンター カズ
Z会の学習サポートセンターで、日夜会員のみなさんからの質問相談に応じている。
















