どーんとこい!中学入試の算数
第33回 「ゴールから逆算する」筑駒の類題
2019.9.26
6.8K



大人でもちょっと手こずってしまうような、難問奇問が続出する中学入試の算数。
でもだいじょうぶ、コツさえつかめば怖くありません!
学習サポートセンターのカズが、算数を楽しく学ぶ方法を伝授します。
算数の問題を解いていて、「どうやったらこんな解き方を思いつくのだろう」と思ったことはありませんか? 算数の解説に出てくる解き方が「突拍子もない発想」に見えたときは、ゴールから逆算してみるとうまくいくことがあります。
同じような考え方ができることはほかにもあります。たとえば、迷路。ふつうはスタートからゴールをめざしていきますが、ゴールからスタートをめざしてみると、始めは思いもつかなかった経路が正解だった、ということがあります。また、Z会の勉強でも、「月末までにてんさく問題をすべて出す」というゴールから、「○日ごろまでにここまでやる」「すると、今日はここまで終わらせないと」のように、逆算して計画を立てるとうまくいきます。
このように、スタートから考えてうまくいかないときには、ゴ-ルから考えるというのは、問題解決のひとつの方法です。
今回は、筑駒の類題を出題します。「2019」などの大きな数を使う問題の場合、周期性や約数に着目することが多いのですが、今回の問題はそういうタイプの問題ではありません。ヒントを参考に、「ゴールから逆算して」解いてみましょう。
問題
2048cmの線分ABについて、以下のような作業を繰り返して、点をとっていきます。
1回目:AとBの真ん中を1とします。
2回目:Aと1の真ん中を2、1とBの真ん中を3とします。
3回目:Aと2の真ん中を4、2と1の真ん中を5、1と3の真ん中を6、3とBの真ん中を7とします。
これを図示すると、以下のようになります。

同じようにして、位置に名前(A,B,1,2,3,…)のついている2点の真ん中に、左から順に番号をつけていくようにして、2047までの数の位置を決めていきます。
このとき、点Aから2019までの長さを求めなさい。また、点Aから2020cmのところにある点の番号を求めなさい。
|
ヒント 冒頭に書いた「ゴールから逆算する」を試してみましょう。この問題では、1から順番に考えるのではなく、2047から考えていくということです。 なお、この問題を考えるにあたっては、1回目は「1」、2回目は「2,3」、3回目は「4,5,6,7」、4回目は「8,9,10,11,12,13,14,15」,……と、各回の最初の数が1,2,4,8,…のように2倍ずつになっていることに気づくことが重要です。そして、1024~2047では2cm間隔、512~1023では4cm間隔になっていることを押さえましょう。 (参考) |
解答・解説はこちら
解答
2点ABの間に入る番号は、1から2047です。
ヒントにも書いたように、各回の最初の数が1,2,4,8,…のように2倍ずつ増えています。そして、2019は2047に近い数であり1024~2047の中にある数です。そのため2回目以降の「番号の個数」と「各番号間の距離」について調べると次の表のようになります。

各回の最初の数は、3回目が2×2=4、4回目が2×2×2=8になっています。したがって、1024は2を10回かけたものだから、11回目の最初の数が1024ということがわかります。
また、「番号の個数」は2倍ずつ増え、「各番号間の距離」は半分ずつ減り、その積が2048で一定であることから、1024~2047および512~1023は次の表のようになります。

なお、両端については、11回目であれば2cmの半分の1cm、10回目であれば4cmの半分の2cmの間が空きます。
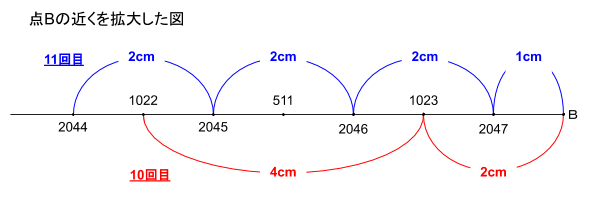
つまり、1024~2047は2cm間隔で並んでいますので、2019から点Bまでの長さは、2019から2047までの長さに1cmをたした長さになります。
したがって、点Bから2019までの長さは
(2047-2019)×2+1=57(cm)
であり、点Aから2019までの長さは
2048-57=1991(cm)(答)
※(2019-1024)×2+1=1991と計算してももちろん正解です。
次に、点Aから2020cmの位置にある点は、点Bから28cmの位置にある点です。ここで、
・1024~2047は、2047と点Bが1cm、あとは2cm間隔。
・512~1023は、1023と点Bが2cm、あとは4cm間隔。
・256~511は、511と点Bが4cm、あとは8cm間隔。
したがって、点Bから28cmの位置にある点は、28=4+8×3より511から前に数えて4番目の数になります。
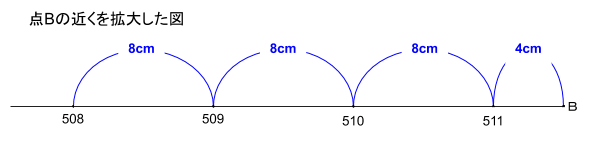
よって、求める答えは
508(答)
この問題を解くにあたってのポイントは、2019は2048に近い数字であるという感覚です。この感覚をもっていると、2019を1024から数えるのではなく、2047から数えたほうが計算がラク、という発想ができるのです。
今回は以上でおしまい。それでは、また来月にお会いしましょう。
「さぽナビ」中学受験コース向け記事 アンケート
本アンケートは、「さぽナビ」中学受験コース向け記事において、より充実した情報提供のために役立てさせていただきます。
ぜひ、中学受験コースを受講している皆さまの声をお聞かせください。
まだZ会員ではない方
プロフィール
出題・文
学習サポートセンター カズ
Z会の学習サポートセンターで、日夜会員のみなさんからの質問相談に応じている。
















