小田先生のさんすう力UP教室
展開図を組み立てよう
2018.1.25
28K


さんすう力を高めるにはどうしたらいいの? まあ、そんなに難しく考えないで、まずはお子さまと一緒に問題に取り組んでみましょうよ。
![]() こんにちは、今年の目標も「文化的な生活」に決めた小田です。去年もそんなことを言っていたわりには、仕事ばかりしていたような気がするので、今年こそは仕事以外のこともがんばりたいと思います。まずはやはり「100名城スタンプ」集めですね。去年は2つしか集められませんでしたし。今年は5つくらい行けるといいな、と思っています。
こんにちは、今年の目標も「文化的な生活」に決めた小田です。去年もそんなことを言っていたわりには、仕事ばかりしていたような気がするので、今年こそは仕事以外のこともがんばりたいと思います。まずはやはり「100名城スタンプ」集めですね。去年は2つしか集められませんでしたし。今年は5つくらい行けるといいな、と思っています。
さて、今回は立体図形の問題です。ちょうど1年前も同じく「展開図を組み立てよう」というテーマで書きました。その際は“センス”を主軸にお伝えしましたが、今回は技術的な面からアプローチしたいと思います。
それではさっそく問題に行ってみましょう。
Stage35:展開図を組み立てよう
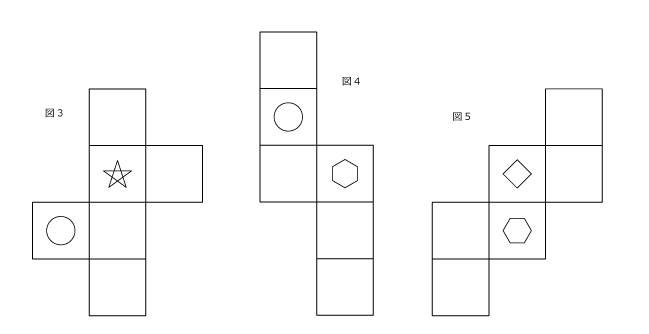
図1と図2の展開図を組み立てたときに同じ立体になるよう、図2の空いている面に模様を入れてください。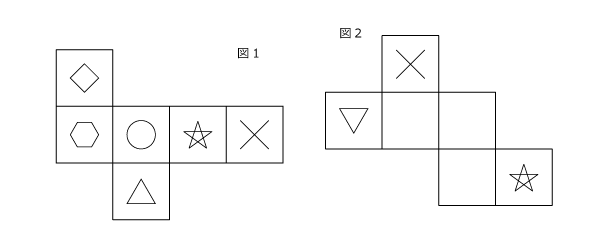
指導のヒント
まずは問題の意味を確認してあげてください。といっても、書いてある通り、「2つを組み立てたときに同じになるようにする」というだけの話ではありますが。
今回は、かなりの難問です。まずは好きなように解かせてあげればいいと思いますが、最初から上手くできなくてもかまいません。
慣れないうちは、印刷したものに答えを書き込んでみて、それを実際に切り取って組み立てるのがよいでしょう。「正しくできているかどうか」を自分の目で判断して納得することも、ひとつ大事なことです。
技術的なアドバイスについては、後述の「さんすう力UPのポイント」をご参照ください。
解答
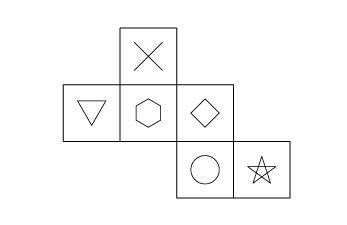
さんすう力UPのポイント
「指導のヒント」にも書いたように、今回はかなりの難問です。慣れていない子であれば、切り取って実際に組み立ててみるだけでも十分でしょう。しかし、ある程度慣れてきた子であれば、もう一つ、考えてほしいことがあるのです。
図形の問題は、よく「センスが必要」と思われがちです。それは、ある面ではまちがいではないのですが、しかしだからと言って、「センスがすべて」というわけでもありません。実際、学年が上がって問題が複雑になってくると、それまで“センス”だけで順調に学習を進めてきた子が急にできなくなる、ということもしばしば起こります。それはやはり、センスだけでなく“算数・数学の技術”を習得していかなければ、“算数・数学の学習”にはならないからです。
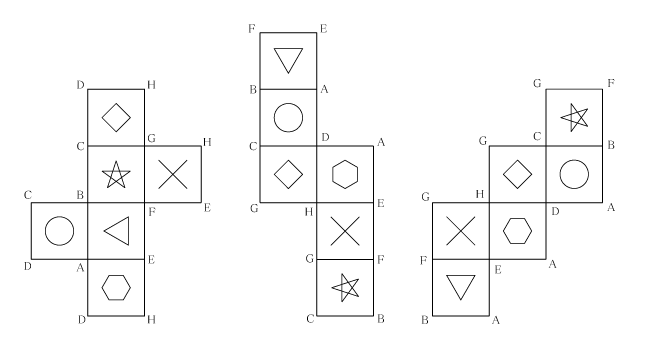
たとえば、今回の問題で重要になる“技術”の一つは「名前をつける」という方法です。立体の面をそれぞれ“面”のままで考えると、脳内で扱う情報の量が多く、難しいです。そこで、各面の頂点に“名前をつけて”みましょう。
下の図アの「〇が書かれた面」に注目してください。この面の頂点を、左下から順に、反時計回りにA、B、C、Dとしました。次に、図イのような「組み立てた立方体」の図を書きます。この上の面を「○が書かれた面」、つまり「面ABCD」とします。ついでに、残りの4つの頂点もE、F、G、Hと“名づけ”ましょう(Hは図イでは見えていない場所、つまり、奥にある頂点です)。
再び図アに戻り「面ABCD」の“隣の面”を見ると、辺ABを共有しているのは△の面、辺CBを共有しているのは☆の面ですね。つまり、図イの面AEFBは△の面、面BFGCは☆の面とわかります。形の向きについては、△は「辺ABのほうが上側」、☆は「辺CGのほうが上側」です。低学年向けの記事にも書きましたが、こうして“言葉”にしていくと、図形のままで考えるよりも考えやすくなりますね。
あとは、図アの各頂点がそれぞれA~Hのうちのどの頂点か、埋めていけばいいでしょう。×の面は今GとFの頂点までわかっているので、「GとFを頂点に持つ☆以外の面」を図イから探すと面GFEHが見つかります(図イの底面)。他の面も同じように埋めていくと、最終的には図アに書き込んだようになります。
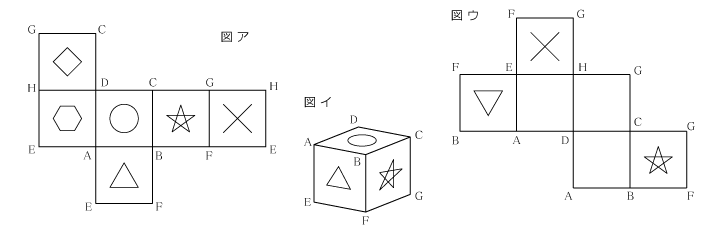
さて、次は、同じように「問題の図2」にも頂点の名前を書き込んでいきます。☆の面は左上から反時計回りにC、B、F、Gなので、そこのあたりからヒントにしていきましょう。こちらも、順番にやっていくと、図ウのようになるはずです。少し面倒ではありますが、丁寧に作業をしていきましょう。
そこまでできたら、最後は順に面の模様を書き込んでいくだけです。「〇はABCDの面」「六角形はADHEの面、ADやHEがとんがっているほう」という感じで書いていけば、“正解する”ことはそれほど難しくはないでしょう。
頂点に名前をつけてそれを順に追いかける、というのは、作業としては面倒かもしれません。しかし、丁寧にやっていけば正確に答えを出すことができます。逆に、感覚的にやっていけば、うまくいくときは楽ですが、それが正しいかどうかは少し怪しいときもあるでしょう。算数・数学には、「“正しいこと”を知りたいときに、計算などの多少面倒な作業をするだけで、その“正しいこと”にたどり着くことができる」という側面もあります。その意味では、算数・数学は“センス”をもたない人のための武器にもなり得る、ということです。そういった、「算数・数学の道具としての意義」を感じてほしい、というのが今回の問題のねらいです。
もっと問題
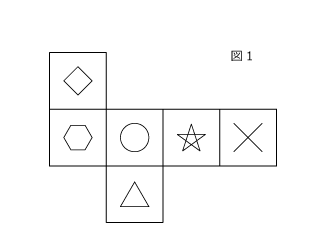
図3~5の展開図について、組み立てたときに図1の展開図を組み立てたものと同じになるよう、空いている面に模様を入れてください。(図1の展開図は、上の例題のものと同じです。)
- 解答
(頂点の配置は、例題の図ア、図イと同じです。)
![]() いかがでしょうか。
いかがでしょうか。
お正月には兄の家に遊びに行き、1歳になった姪に遊んでもらってきました。姪は新しくもらった玩具を開けて遊び始めたのですが、子どもってすごいですね。好きに遊ばせると、自分で「こうしてみよう」と考えて遊び方を工夫し始めるんですね。しかも、試行錯誤しながら、少しずつ遊び方がうまくなっていっていました。彼女のなかでは何かやってみようと思ったことがあったようで、途中で「できたー!」とうれしそうにもしていました。そうやって、何かしらやってみたいことがあって、いろいろとやってみて、できたときにうれしくなる気持ちが、「勉強」の原動力になるのでしょうね。同時に、それは算数などの「勉強」でも同じことで、その子どもの「勉強」を邪魔しているのは、周りの大人の「うまくできてほしい」という欲なのかもしれない、と反省した次第です。
それではまた来月!
|
文:小田 敏弘(おだ・としひろ) 数理学習研究所所長。灘中学・高等学校、東京大学教育学部総合教育科学科卒。子どものころから算数・数学が得意で、算数オリンピックなどで活躍。現在は、「多様な算数・数学の学習ニーズの奥に共通している“本質的な数理学習”」を追究し、それを提供すべく、幅広い活動を展開している(小学生から大人までを対象にした算数・数学指導、執筆活動、教材開発、問題作成など)。 公式サイト:http://kurotake.net/ 主な著書
|
















