こんにちは、最近忘れ物が多い小田です。事務所以外でも授業をしているので、そちらで使うものはそちら用にカバンを作ってまとめているのですが、そうすると、パスケースや携帯電話などを入れ替え忘れたりするんですよね。よく生徒が「塾用のカバンで来たので筆箱入れるの忘れました！」と言ってくるのですが、その気持ちが十分理解できるので、あまり厳しくは叱れません。
　さて、今回は「公約数・公倍数」に関するお悩みです。このあたりは、学校のカリキュラムの構造上、つまずく人がある程度出てくるようになっているな、と感じる部分でもあります。実際に、悩んでいる方もたくさんいらっしゃるでしょう。少しでもそういった方々へのヒントが示せたらいいな、と思います。
　それでは早速行ってみましょう。

　“足し算と掛け算の関係”には、実はとても難しい部分があります。そう言うと、いやいや足し算をまとめたものが掛け算じゃないの、と思う人もいるでしょう。もちろん、掛け算にはそういった側面もありますが、よくよく見てみると、それだけではない世界も広がっているのです。
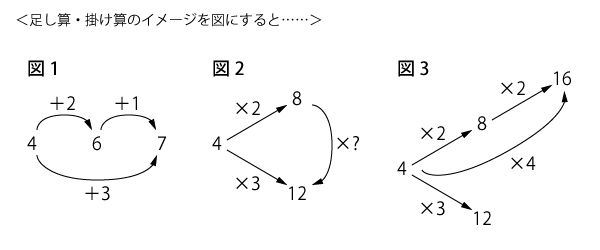
　たとえば、4に2を足すと6で、3を足すと7ですね。4に2を足して6にしたけど、やっぱり7にしたいな、と思ったときには、さらに1を足せば7にすることができます（図1）。しかし、掛け算ではどうでしょうか。4に2をかけると8で、3をかけると12です。2をかけて8にしてしまったあとでやっぱり12にしよう、と思っても、整数をかけるだけでは8を12にすることができません（図2）。
　そういうふうに見てみると、“直線的”な足し算の世界と違って、掛け算の世界は“分岐している”と捉えることができませんか。

　約数・倍数の学習をする、というのは、このような“掛け算の世界”という全く新しい世界に入っていく、ということでもあります。本来なら、そういった場面では十分に時間をかける必要があるでしょう。とくに、この“掛け算の世界”は新しいだけではなく、難しい部分も含まれています。
　一直線ではなく分岐している、という話をしましたが、その様子も単純ではありません。4に2をかけて8にしたあと、4×4の16にしようと思ったら、「さらに2をかけ」ればできてしまいます（図3）。「×3」は「×2」の先になくても、「×4」は「×2」の先にあるわけですね。“掛け算の世界”を自由に探索するためには、そういった分岐の様子についても理解を深めていく必要があるのです。

　しかし、そうやって習得に時間をかけたい内容であるにもかかわらず、率直に言えば、学校のカリキュラム上ではその“新しい世界”に慣れるための時間が十分にとられているとは思えないのが現状です。ひとつには、限られた時間の中でなるべく多くのことを学ばせたい、という、学校教育というシステムそのものからくる制約もあるでしょう。学校のカリキュラムの中での「約数・倍数」の扱いを見てみると、「分数の約分・倍分、通分で必要になるから、その準備として触れる」というふうな位置づけをされている印象があります。約数・倍数の言葉の意味（定義）の説明や、公約数・公倍数の求め方の技術的な指導はもちろんありますが、そこから“掛け算の世界”への理解を深めていく時間、というのは、実際にはほとんどとれていないのではないでしょうか。

　その意味で、冒頭でもお伝えした通り、この公約数・公倍数に関しては、カリキュラムの構造上の問題で、多くの子がつまずいてしまう部分です。今回のお悩みのように「3つの数の公約数・公倍数を求めるのが難しい」や「文章題でそういう考え方がでてこない」というのは、まさに典型的な話で、理由としては、これもお悩みの中でもおっしゃっている通り、やはり「意味をしっかり理解していない」ということなのでしょう。しかし、それは珍しいことではなく、そもそもそういう子が発生しやすい状況がある、というのは、まずご理解いただければと思います。

　そういうわけで、約数・倍数あたりで引っかかるのは、言ってしまえば「仕方ない」という話ではあるのですが、そうは言っても、実際問題として分数の通分に必要である以上、それで済むわけでもないでしょう。ただ、つまずく原因が明らかである、ということは、対処法もシンプルである、ということではあります。つまり、じっくりと“掛け算の世界”への理解を深める時間をとる、というのが一番の正攻法です。

　こういった掛け算の世界の分岐を理解しようとしたとき、カギになるのが「素数」という数です。2や3や5、7のような、「(1を使わずに)これ以上掛け算の形に分解できない数」のことを素数と言いますが、その素数によって“掛け算の世界”は構成されています。「2」と「3」は別の素数なので“別々の道”に進みますが、「4」は「2×2」なので、“同じ道”の先にあるのです。まずはこの素数と慣れ親しむ、というのが、掛け算の世界を理解するための第一歩です。

　素数に慣れてきたら、次は数をその素数に分解していく練習をしましょう。たとえば、12はまず3×4という掛け算に分解できますね。ここで出てきた数について、3は素数なのでこれ以上分解できません。4はまだ2×2に分解できます。2は素数でこれ以上分解できないので、ここでおしまいです。12＝3×2×2と分解することができました。このように、数を素数だけの掛算に分解していくことを「素因数分解」と言いますが、この「素因数分解」こそ“掛け算の世界”で数をとらえる重要な視点なのです。

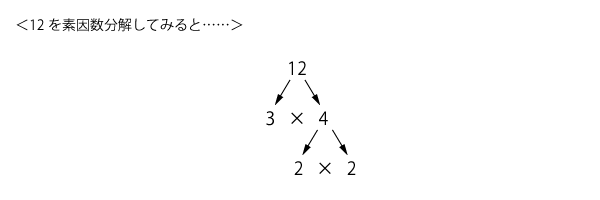
　公約数・公倍数を計算していく際にも、この素因数分解は欠かせません。たとえば、12と18の公約数や公倍数を求めたいとします。そんなときは、まず12と18を素因数分解してみましょう。12＝2×2×3、18＝2×3×3です。公約数を探す、というのは、「12＝○×□、18＝○×△としたときに、○に共通して入る数を探す」ということでもあるので、それぞれ分解して出てきた素数（素因数）に注目すれば、公約数は見えてきます。○には2や3を入れることができますね。2と3を両方1個ずつ入れると考えて、○を6にすることもできるでしょう。素数を一つも入れないという選択肢もあり、その場合、○は「1」と考えます。この中で一番大きいのは、共通しているものを最大限入れた「6」ですが、これが最大公約数です。

　さらに言えば、公倍数を探すのは「12×△＝18×□となるような数を探す」ということです。これもやはり素因数に注目すると、お互い「相手が持っているのに自分が持っていない数」をかけてあげればいい、とわかります。つまり、18は3を2個持っていますが、12は1個しか持っていないので、12に3をかけてあげるのです。逆に、12は2を2個持っていますが、18は1個しか持っていないので、18には2をかけてあげます。そうすると、両方とも36になりますね。これが最小公倍数です。最小公倍数以外の公倍数は、さらに両方に同じ数をかけてあげればいいでしょう。

　3つの場合も基本的には同じです。それぞれを素因数分解したあと、共通部分を取り出すのが「最大公約数」、足りないものをかけてあげるのが「最小公倍数」です。たとえば、12と18と30の最大公約数・最小公倍数を求めてみましょう。それぞれ、素因数分解すると以下の通りです。全員に共通しているのは「2と3が1個ずつ」なので、最大公約数は「6(＝2×3)」でしょう。また、12に3と5、18に2と5、30に2と3をかけると素因数の個数がそろうので、最小公倍数は「180(=12×3×5など)」となります。

　3つの最大公約数・最小公倍数を求めるには、あともうひとつ、重要な考え方があります。それは「2つずつで考える」、という方法です。たとえば、12と18と24の最大公約数を求めるとき、12と18の最大公約数を求めて（6ですね）、それと24との公約数を求める、と考えるのです。最小公倍数も同様に求められます。この方法のメリットは、慣れると暗算でできるようになり、スピードが格段に上がる、というところでしょう。また、「12と18と24」のような組み合わせであれば、24は12の倍数（12は24の約数）なので、最小公倍数を求めるときには「12と24で24、18とその24で72」とすることもできます。つまり、実質的には「2つの最小公倍数」を求めるだけで済むときもあるのです（もちろん、この考え方をスムーズにできるようになるためには、“掛け算の世界”に慣れ親しんでおく必要があるのですが）。

　いずれにしても、学校の授業で初めて“掛け算の世界”に触れた場合、すぐにその世界を自由に探索できるわけではないでしょう。公約数・公倍数を求めるのも、なかなかスムーズにはいきません。しかし、焦らなくても大丈夫です。まずはいろんな数を、掛け算の形に分解したり、元に戻したりする経験を積んでみましょう。そうして新しい世界に慣れ、新しい世界を見る視点を育てていくのです。そうやって、新しい世界の深さに触れることができれば、公約数や公倍数を求める計算も楽にできるようになるでしょう。

　　いかがでしょうか。

　そんなこんなで、今年度も1年間どうもありがとうございました。最近は時の流れも速く感じるようになり、今回もあっという間の1年間だったような気がします。年度が替わると、生徒たちの学年も1つ上がるわけですが、そうやって生徒たちがどんどん成長していく姿を見るのが、毎年の楽しみです。「もう○年生になったのか！　大きくなったなあ！」というのは、“おっさん”の定番のセリフではありますが、気にせず繰り返し使っていきたいと思います。

　一応はこれで一区切りですが、また来年度も変わらず連載させていただきますので、引き続きよろしくお願いいたします。

　それではまた来月！