こんにちは、最近は昔の歌をよく聞いている小田です。月並みな話ではありますが、昔の歌を聞いていると、その歌をよく聞いていたころの空気感が蘇ってくるのがいいですよね。そしてその懐かしい気持ちに浸れる一方で、昔はよくわかっていなかった歌詞の意味がわかるようになったりと、新しい発見があるのもよいです。

さて、今回のお悩みは「分数の割り算」についての内容です。「なぜひっくり返してかけるのか」と疑問に思ってしまい、そこから先の学習に進みづらくなってしまう子も多いでしょう。この“お悩み”は簡単に解決するものでもありませんが、可能な範囲でお役に立つお答えができれば、と思います。

それでは早速行ってみましょう。

分数の単元は、算数の学習のなかでも多くの子がつまずいてしまう内容のひとつでしょう。とくに、その割り算の習得においては、「なぜひっくり返してかけるのか」という疑問をもちやすく、納得がいかなくて学習が進められなくなってしまう子や、納得がいかないままに学習を進めてよくわからなくなっていく子が多くでてきます。このハードルをうまく越えられるかどうか、というのは、実質的に「算数・数学の学習をうまく進めていけるかどうか」に大きな影響を与えるわけですが、しかしここで気をつけてほしいことがあります。それは「わかりやすい説明」を求めないことです。

今回のお悩みを根本からひっくり返すような話になってしまいますが、ただやはり、「わかりやすい説明を求める気持ち」が、逆に理解の妨げになっていることは、実際にはよくあります。その理由はいたってシンプルで、「わかりやすい説明」なんて存在しないからです。

すでに何度かお伝えしていることですが、算数の学習を進める、新しい概念を身につけていく、というのは、そもそもとても難しいことです。そのなかでもとくに、分数（小数もですが）は難しいのですが、その難しさの本質は、「新しい世界に進む」難しさです。

2018年6月号・7月号でもお伝えしたように、分数や小数を学習すると、「数の世界」がひとまわり広がります。より広い世界へ進んだとき、それまでの世界で通用していた感覚が通用しなくなる場面が多々あります。そのギャップこそが「わからなさ」の正体なのです。日本で暮らしていた人が、初めて海外に行ったときと同じようなものです。勝手が違って戸惑うことがたくさんある、というのは、想像がつくのではないでしょうか。国外のことを本当に理解しようと思ったら、まずは実際に出かけてみるのが一番です。国内にいるまま、「説明」だけを聞いてもわかったような気になるだけでしょう。算数の学習でもそれは同じです。新しい世界のことは、実際に新しい世界でいろいろ経験を積みながら理解していくしかありません。今までの世界（「自然数」の世界）にいるままで、わかりやすい「説明」を求めるだけでは、結局はわかったような気にしかならないのです（裏を返せば、指導者が「うまく説明してあげよう」としてしまうことも、学習者を今までの世界にとどめたままにしてしまい、理解の妨げになってしまいます）。

新しい世界では、今までの世界と違うことが起きます。そのギャップに出くわしたとき、必要なことは「考える」ことです。今までの世界と同じようにできることは何か、同じようにできないことは何か、同じようにできないなら、どう調整すればいいのか。そういったことを「考える」ことが、学習を進めていく際に重要な姿勢となります。たとえば、今回のテーマである「分数の割り算」の話をすれば、「そもそも割り算とは何か」「どういう場面で割り算を使えるのか」をもう一度じっくり考えたりするのもいいでしょう。「6個のリンゴを3人で分けたときに1人あたり何個ずつになるかを考える」というのは、「割り算を使う場面」のひとつですね。3つのお皿を用意して、そこにリンゴを置いていくイメージでしょうか。確かに、このイメージで分数の割り算を捉えようとすると、「わからない」となってしまいがちかもしれません。「6個のリンゴを2/3人で分ける」と言われても、少しピンときませんね。しかし、このイメージであっても、「割られる数のほうが分数の割り算」は考えることができます。「2/5÷3」を「2/5切れのパンを3人で分ける」と考えるとどうでしょう。倍分（約分と逆の操作）して2/5を6/15とすれば、3人で分けると1人あたりは2/15切れずつになります。「1/5切れが2つ」を切り分けて「1/15切れが6つ」として、それを2つずつ配っていく、という感じですね。

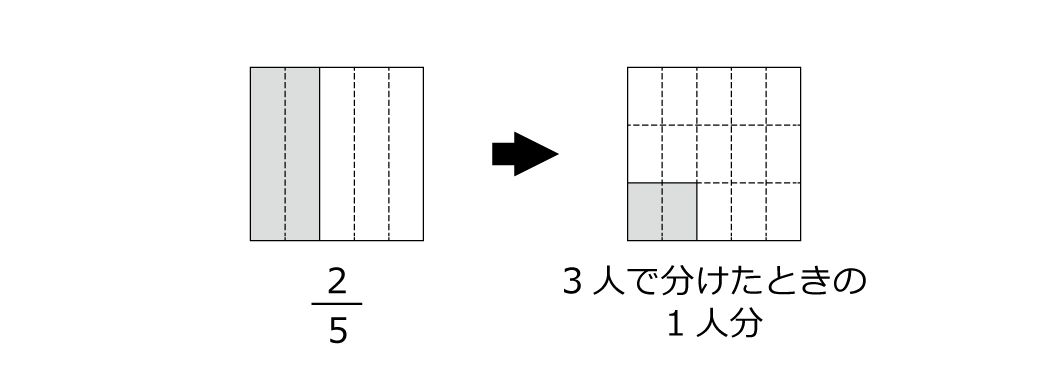
ほかにも、「割り算を使う場面」には、「6Lの水を2Lのバケツに分けると何個のバケツに分けられるかを考える」というものもあります。6から2を繰り返し引いたときに何回引けるか、と考えているわけですが、こちらのイメージなら、「分数で割る」というのも考えられなくはありません。「6/7Lの水をひとり2/7Lずつ飲むと何人分になるか」と言われたら、「3」と答えるのはそう難しくはないのではないでしょうか。もう少し複雑にして「3/5Lを2/10Lずつに分ける」としても、先ほどと同じように倍分して3/5を6/10とすれば、やはりこの答えも「3」とわかりますね。
ただ、このイメージでは「小さい数を大きい数で割る割り算」を考えようとすると、「引いていけない」となってしまいますし、そもそも答えが整数で出てこない計算には使えなさそうな感じがします。
それでは、「小さい数を大きい数で割る」場面や、「答えが整数にならない」場面で、割られる数も割る数も分数にできそうなのは、どういう状況でしょうか。本当はそれを自分なりにいろいろと“考えて”ほしいわけですが、ひとつ例をあげてしまうと、「単位あたりの量を求めるとき」が考えられます。
「3時間で6km進んだとき、1時間あたり何km進んだか」を考えると、「6÷3」で「2」と答えますね。これを「3/4時間で2/5km進んだとき、1時間あたり何km進んだか」とすると、「2/5÷3/4」という割り算になるはずです。この答えを考えてみましょう。まず、3/4時間で2/5km進んだ、ということは、1/4時間で進んだ距離は2/5÷3となるはずです。この計算の結果は、先ほどパンの例でやったように、2/15ですね。1/4時間で2/15km進んだということは、1時間で進んだ距離は2/15×4で8/15kmとわかります。つまり、「2/5÷3/4」の計算結果は「8/15」ということです。

こうやっていろいろと「割り算を使う場面」を“考えて”いくと、別に「ひっくり返してかけ」なくても、計算の種類によっては「分数の割り算」ができることもある、ということに気づきませんか。
「分数の割り算はひっくり返してかける」というのは、実は「唯一絶対の方法」ではありません。ただ、いろんな「分数の割り算」の場面を考え、その構造を一般化していった結果、「そうするとどんな“分数の割り算”でも同じように計算できる」というだけに過ぎないのです。その意味では、「なぜ分数の割り算はひっくり返してかけるのか」とう質問の答えは、身もふたもない話をすれば「（結果的には）そうするとうまくいくから」ということでしかありません。しかしそれを「これが分数の割り算の正しいやり方だ！」というふうに提示してしまうと、「なぜそうなるの？」と疑問に思ってしまい、スムーズに受け入れられなくなってしまいます。まずは自分でいろんな“割り算”を考えて、いろんな方法でやってみる経験を積んで、そうして「どれも結局“ひっくり返してかけた”結果と同じになっているな」と確認できれば、「分数の割り算はひっくり返してかける」という結論が腑に落ちてくるでしょう。

“教える”側に立つ場合、大事になるのは「うまく説明してあげよう」とすることではなく、そういったことを「一緒に考えてあげよう」「考えるためのヒントをあげよう」という姿勢です。今回あげた「いろいろな割り算の例」も、一方的に「こういうときはこう」と“説明”してしまうと、やはり子どもには受け入れてもらえません。「（今まで）割り算はどういう場面で使っていた？」「それを分数にするとどうなる？」「そもそも分数にできる？」「分数にできる割り算はどういう割り算？」という感じで声をかけてあげてください。正しい場所へ導いてあげようとするのではなく、新しい世界をお子さまが安心して探検できるよう、温かくサポートしてあげることが大事なのです。

ちなみに、「5分の1割る5分の2」と「5分の1かける2分の5」の答えが一緒になるのはどうしてですか？という最初の質問への答えは、「そうなるんです。不思議ですよね」となってしまいます。自然数の世界では「ある数に対して、何かをかけたときと何かで割ったときで答えが一致する」ということはありませんでしたが、数の世界が広がって分数小数の世界にいくと、「そういうことも起こる」というだけの話です。「なぜ」と考えるよりも、「不思議だな・おもしろいな」と捉えるほうがよいでしょう。そういった「新しい世界」の「新しい性質」は、「新しいこと」をやるために利用できます（分数の割り算で「ひっくり返してかける」ことも、この性質を使っていますね）。算数の学習を進めることを、ぜひ「新しいことができるようになる」喜びにつなげていってほしいな、と思います。

　いかがでしょうか。
3月にリニューアルした『東大脳さんすうドリル　計算編』に引き続き、同シリーズの『図形編』もこの7月にリニューアルいたしました！ 図形の“感覚”を磨いていくためには、「実際に図形と触れ合うこと」と「基本的な図形と慣れ親しむこと」が重要なのですが、それらの要素をしっかり凝縮したドリルになっているのではないか、と自負しております。低学年でこれから図形の学習を進めていきたいお子さまだけでなく、高学年ですでに図形に苦手意識をもってしまっているお子さまにも、ぜひ楽しんでいただきたい一冊です。よろしくお願いいたします。

それではまた来月！