こんにちは、暑さに弱い小田です。毎年言っている気がしますが、今年も暑いですね。しかも今年は本格的に暑くなるまでに、暑かったり寒かったりをくり返していた時期もあったので、衣替えのタイミングがわからず、なんだかんだで未だに冬用のジーパンをはいています。この暑い中、本当にそれで大丈夫かなと思うこともありますが、意外とクーラーの効いた部屋で過ごす時間も多いので、それほど困ってもいないような気はします。むしろ、冷え性の私にとっては、必要以上に下半身が冷やされないので逆に過ごしやすいかも、と思ったり。

さて、今回は「図形」についてのお悩みです。とはいえ、実はこのお悩み、掘り下げていくと図形以外の分野にも通じるテーマがあると思いますので、そのあたりにもしっかりお答えできればいいな、と思います。

それでは早速行ってみましょう。

“カンタンなこと”に苦戦する子どもを見ていると、「こんな簡単なこともできないなんて、この子は大丈夫なんだろうか」と不安になってしまいますよね。しかも、ご自身が算数に苦手意識をもつ方だと、「算数が苦手な自分でも、これくらいのことはわかる・できるのに、それさえわからない・できないこの子はどれだけ算数ができないのだろう」と絶望してしまうこともあるようです。

そういった心配・不安を感じている保護者の方に対して、まず声を大にしてお伝えしたいことは、「算数の学習に“カンタンなこと”なんてない」ということです。大人が”カンタン”と思うことのほとんどは、「子どもにとっては難しいもの」です。苦戦することはむしろ当たり前なので、不安になったり焦ったりする必要はありません。

今回のお悩みの、「違う形どうしの区別をつける」というのは、まさにそのひとつでしょう。1・2年生向けの「さんすう力UP教室」では2019年5月号「図形のセンスを身につけよう」や2019年8月号「同じ模様を探してみよう」でもお伝えしたことなのですが、そもそも人間は“物の形”をそこまできちんと見ていません。大人でも、たとえば電車に興味のない人はどの電車を見ても「同じもの」に見えていると思いますし、車に興味がない人にとってはどの車も「同じもの」に見えていると思います。もちろん、それ自体は別に悪いことではなく、むしろ自然なことでしょう。視覚から入ってくる情報はとても情報量が多いので、すべてを認識しながら生きていると、それはそれでとても疲れてしまいます。ただ、そうやって無意識のうちに情報を選別している、視界に入っていても“見ていない”情報がある、というのは、忘れてはいけない事実です。

図形の学習の重要な要素の一つに、その「あまり普段細部まで見ていないもの」を「しっかり見る練習をする」というものがあります。ひとくちに三角形・四角形と言っても、いろいろな種類の三角形・四角形があります。それらの細部に注目し、同じ特徴をもつもの同士でグループを作っていく、というのが、そもそも「図形の学習」なのです。その意味では、「同じように見えている」というのは、単に「まだ学習を進めていない」というだけであって、つまり「これから学習を進めていけばいい」というだけの話です。大人にとって“カンタン”に見える、というのは、単に「すでに学習を済ませている」からです。もし自分が算数が苦手だったとしても、小学生の子どもの何倍もの人生を生き、何倍もの経験を積んでいるということを忘れてはいけません。

子どもが「同じものに見える」と悩んでいるとき、一番やってはいけないのは、そう見えている「その子の見え方」を否定することでしょう。あくまでその子にとってはそう見えているのであり、それを否定してもその子が傷つくだけになってしまいます。そうして「自分は苦手なんだ」という思い込みをもってしまうと、そこから先の学習を諦めることにつながってしまうでしょう。それはやはり一番避けたい状況です。

重要なことは、まずはその「子どもが見ている世界」を、そういうものなのだと受け入れてあげることです。そして「確かによく似ているよね」と共感してあげることです。そうやって“これからの学習”を温かく見守ってあげることが重要なのです。

図形の学習に限らず、「同じように見えていることに区別を与える」のは、算数の重要な役割のひとつです。子どもたちを見ていておもしろいと思ったことの一つに、「子どもたちは足し算もかけ算も“と”で表現している」ということがあります。「3＋5＝8」は「3と5で8」、「3×5＝15」は「3と5で15」というような感じです。そうすると、複雑な計算をしている途中で、足すべきところをかけてしまったり、逆にかけ算のところを足し算してしまったり、というミスがでてきます。もちろん、その状態が悪いというわけではありません。しかし、そういう子たちにとっては、足し算もかけ算も「2つの数を組み合わせる計算」という認識であり、その境界線が曖昧なのだと思います。その状態から、それらの境界線を明確に認識し、「足し算」と「かけ算」の概念をそれぞれ自分の中で確立していくことが、“算数・数学の学習”なのです。

学習を進めていくうえでは、区別のつけ方だけでなく、区別をつける意義を伝えることも大事でしょう。図形の話に戻ると、たとえば「台形」は「向かい合う辺のうち、少なくとも1組が平行な四角形」と定義されます。下の図のなかでいうと、まず(あ)の形はいわゆる“台の形”なので、抵抗なく台形と呼べますね。(い)は上の辺の方が長く、“台”にすることは難しそうですが、上下の辺が平行なのでこれも定義の上では台形です。(う)も、縦に向いていますが、左右の辺が平行なので台形で、(え)は正方形ですが、上下の辺が（左右の辺もですが）平行なので、台形のひとつということもできます。しかし、これらの図の中で(お)の形だけは、平行な線の組をもたないので、これだけは台形ではありません。形で言うと(あ)に一番似ているのに、これだけが仲間外れなのです。

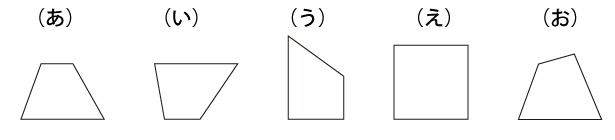
なぜ、（あ）～（え）を同じグループにして、（あ）と（お）は違うグループのものとするのか、それは、「同じように扱える部分・扱えない部分」がそれぞれあるから、というのが大きな理由です。たとえば、それぞれの面積を求めようとしたとき、平行な辺をもつグループ((あ)～(え))では、その平行な辺をそれぞれ上底・下底として、「(上底＋下底)×高さ÷2」で面積を計算できます。しかし、(お)のような平行な辺をもたない形では、その手法で面積を求めることができません。「台形の面積の公式」を使いこなすためには、「台形」と「そうでないもの」の区別をつける必要がありますし、逆に、その区別がつくようになれば、公式という便利な道具をうまく使えるようになるのです。

普通にしていると区別がつきにくいものに対して区別をつけていく、というのは、それなりに労力が伴います。コストをかけて、その区別を習得していこうとするには、やはりそうするメリットが必要でしょう。それを納得し、前向きに学習を進めていくためにも、区別をつけることで新しいことができるようになる、ということを、折に触れて伝えてあげることが重要です。

細やかな違いを意識の上にのせることができれば、世界の見え方は変わってきます。そうやって、自分の見える世界を豊かにしていく、というのも、「勉強」の醍醐味のひとつです。

これから「勉強」をしていく段階の子たちが、まだまだできない・わからないことがある、というのは当たり前のことでしょう。そういった子たちに対して、センスがない、と不安になってしまうよりも、これまで様々なことを「勉強」してきた人生の先輩として、「世界が豊かになる喜び」をぜひ伝えてあげてください。

いかがでしょうか。

最近、毎日通勤に使っている道のブロック塀が、フェンスに置き換わりました。いわゆる危険ブロック塀というやつだったようです。狭い道だったので、もし通勤中に大きな地震があってそれが倒壊していたら、と考えると、今更ながら背筋の凍る思いがします。しかし実際にフェンスに置き換わったことを見ると、世の中には自分の把握していない問題もたくさんあって、でもそれを解決しようと頑張っている人たちもいて、実際に少しずつ解決されて、そうやって少しずついい社会になっていっているのかな、と感じたりもします。それはそれでうれしいことですよね。自分も、自分の仕事を頑張っていきたいと思った話でした。

それではまた来月！