こんにちは、暑さに弱い小田です。とくに最近は暑いですよね。この暑さだと、そのうちとけてなくなりそうな気もしています。一応、一日のうちの大半は、クーラーを効かせた部屋で授業をしているわけですが、移動などがあるとその都度汗だくになってしまっています。そんな汗まみれの洗濯物の匂いが結構気になっていたのですが、最近、お風呂の湯舟に熱湯をはってその中にしばらくつけておく、という方法を知りました。試してみたところ、実際いい具合に匂いが落ちて、少し感動しました。そういった生活の知恵も、やはり大事ですよね。いろいろ勉強しようと思いました。

さて、今回は物の数を数える問題です。問題としては単純なので、取り組むハードルとしては低いかと思います。しかし、その奥に豊かな世界が広がっている問題でもあるので、そのあたりも含めて、楽しんでいただけるとうれしいです。

それでは早速行ってみましょう。

黒い碁石をならべて、図のような形を作りました。碁石を何個使っているでしょう。

12個

問題の意味はいいでしょう。図の黒い丸の数を数えていくだけです。

答え合わせは「正解・不正解」を伝えればいいのですが、とくに「不正解」の場合は、実際に碁石やおはじきなどを並べてみて、手で触って数えるようにしてみてください。

「正解」の場合は、どういう数え方をしたか、聞いてみましょう。そして、余裕があるようなら、ほかの数え方も考えてみるよう、促してみてください。

黒い碁石をならべて、図のような形を作りました。それぞれ、碁石を何個使っているでしょう。

（1）10個　（2）12個　（3）9個　（4）9個　（5）9個　（6）16個　（7）32個　（8）19個　（9）25個

人類は、物の数を数える中で「数」という概念と出会いました。それは、「数」という字を「数（かぞ）える」と読むことからも明らかでしょう。そして、その「数」という概念を発展させていくことで、算数・数学という道具を確立していきました。その意味では、「数える」というのは、最も原始的な「数学」ということもできるでしょう。

しかし、原始的であれば簡単かと言われると、実はそうでもありません。物の数を数えるのは、それらの個数を正確に知りたいときです。当たり前の話ですが、数えてみたけど数え間違えていた、では、あまり意味がないでしょう。1回数えただけでは、その個数が正しいかどうかわかりません。2回、3回数えてみて、毎回同じ個数ならなんとなく正しい気もしますが、数え直すたびに個数が違うこともよくあるでしょう。そうすると、どれが正解なのかわからなくなり、混乱してしまいます。そもそも、正しい個数が知りたいから数えている、ということは、事前に「正しい個数」がわかっているわけではない、ということです。つまりそれは、気軽に“答え合わせ”ができない、ということを意味します。そう考えてみると、「物の数を正確に数える」というのは、なかなか難しいことだと思いませんか。

物の数を数えるというのは、原始的ではありつつも、意外に難しいことです。うまくやっていくためには、様々な工夫が必要になります。そのアイディアのひとつとしては、たとえば「順番に数えていく」というものがあるでしょう。上から下、左から右、といったように、自分で順番を決めて数えていくと、同じものを重複して数えてしまったり、数えとばしてしまったり、というリスクを少し減らすことができます。

ほかにも、「分けて数える」というアイディアはあります。「解いてみよう」の中でいえば、(1)(3)(4)(5)などは、縦の列や横の段に区切っていくと、数えやすくなるでしょう。分けて数えたあとは足しあわせます。たとえば(1)なら、1+2+3+4=10という感じです。(4)は、縦に区切るのが見つけやすいですが、横に区切って3つずつと見ることもできます。少し見えづらいかもしれませんが、実は(8)も、段ごとに区切れば、3+4+5+4+3=19とすることができます。分けて数えたときに、同じ数ずつあれば、もちろんかけ算も使えますね。(6)は四隅をそれぞれ分けて数えれば、4個のかたまりが4つ、となって、4×4=16となります。

分けて数えていくとき、「分け方」には唯一絶対の正解があるわけではありません。(2)は、図1のように分けて4×2＋2×2＝12とすることもできますが、図2のようにすれば3×4＝12となります。

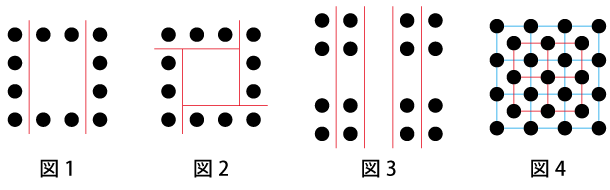
(6)も、図3のように大きく見て列ごとに数えることができるでしょう（これでも4×4＝16ですが）。(9)は段ごとに分けると4＋3＋4＋3＋4＋3＋4＝25という感じですが、図4のように見ると、4×4＋3×3＝25とすることもできます。(7)は、段ごとに数えて6＋6＋4＋4＋6＋6＝32でもいいですし、一周ごとに数えて20＋12＝32とする方法もあります。図5のように分けて4×8とするのもいいでしょう。なお、(7)については、真ん中の空いた部分を後から引く、つまり、6×6－2×2＝32とすることもできます。足し算ができるなら引き算も、というのは、次に重要なアイディアですよね。

物の数を数えることは原始的でありながら、実は難しい作業です。しかし、その難しさゆえに、様々な工夫の余地が生まれます。そうやって、頭を使い、目の前の課題をうまくクリアしていこうとする姿勢が、算数・数学の根本的な姿勢でもあるはずです。その工夫には、もちろんある程度のうまいへたはあるでしょう。しかし、まずは自分なりに工夫してみることそのものが大事です。今回の問題を解く中で、決まった方法にこだわらず、一つの問題に対して自分なりにいろいろと工夫をすることで、算数・数学のおもしろさ、奥深さを体験してくれたらいいな、と思います。

　いかがでしょうか。

最近、毎日通勤に使っている道のブロック塀が、フェンスに置き換わりました。いわゆる危険ブロック塀というやつだったようです。狭い道だったので、もし通勤中に大きな地震があってそれが倒壊していたら、と考えると、今更ながら背筋の凍る思いがします。しかし実際にフェンスに置き換わったことを見ると、世の中には自分の把握していない問題もたくさんあって、でもそれを解決しようと頑張っている人たちもいて、実際に少しずつ解決されて、そうやって少しずついい社会になっていっているのかな、と感じたりもします。それはそれでうれしいことですよね。自分も、自分の仕事を頑張っていきたいと思った話でした。

それではまた来月！