小田先生のさんすう力UP教室
論理の力を鍛えよう
2020.8.27
6.2K


さんすう力を高めるにはどうしたらいいの? まあ、そんなに難しく考えないで、まずはお子さまと一緒に問題に取り組んでみましょうよ。
(執筆:小田敏弘先生/数理学習研究所所長)
![]() こんにちは、無事に引越しを終えた小田です。引越してから、未開封だった食器をすべて開封していっているのですが、その結果、マグカップがたくさん食器棚に並ぶことになってしまいました。コンビニなどでポイントをためるともらえたりするので、ついついもらってしまうんですよね。あと、展示会に行ったときなどに、マグカップならきっと使うだろう、とついつい買ってしまうことも多いです。せっかくなので、アイスコーヒーと豆乳を冷蔵庫に常備して、豆乳オレとかを嗜んだりする毎日です。少し優雅な気分です。
こんにちは、無事に引越しを終えた小田です。引越してから、未開封だった食器をすべて開封していっているのですが、その結果、マグカップがたくさん食器棚に並ぶことになってしまいました。コンビニなどでポイントをためるともらえたりするので、ついついもらってしまうんですよね。あと、展示会に行ったときなどに、マグカップならきっと使うだろう、とついつい買ってしまうことも多いです。せっかくなので、アイスコーヒーと豆乳を冷蔵庫に常備して、豆乳オレとかを嗜んだりする毎日です。少し優雅な気分です。
さて、今回は論理の問題です。本文で詳しく書いていこうと思いますが、「論理」の力の基盤となるのは、「考えられる候補をすべてあげる力」です。「他にはもうないかな」ということを考えながら、問題にチャレンジしてみてください。
それでは早速行ってみましょう。
Stage6:論理の力を鍛えよう
例題
<例題> 図の点Aから点Bまで、点線にそって線を引くとき、線の引き方をすべて書いてみてください。ただし、同じ線や点を2回以上通ってはいけません。遠回りするのは構いません。
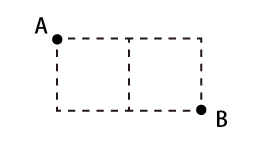
例題の答え

まず、お手数をおかけして恐縮なのですが、最初に「解答欄」つまり道順を書き込む図(問題で与えられた図と同じで構いません)をたくさん用意してあげてください。答えは上記の通り4つですが、「4つしかない」ことがヒントになるとよくないので、多めに用意するのがいいでしょう。
お子さんが問題に取り組み始めたら、問題の意味が理解できているかどうか、確認してあげてください。いくつか自分で見つけられていれば、ひとまず大丈夫です。手が動かない場合は、「AからBまで点線にそっていろんな行き方で行くんだよ」と伝えてあげてください。あとは、取り組んでいる様子を見て、「同じ点・同じ道を2回以上通ってはいけないこと」や「遠回りはしてもいいこと」がわかっていなさそうなら、それらも随時伝えてあげましょう。
答えがいくつか見つかったら、「すべて探す」ことを確認してあげてください。「これで全部」という反応があれば、本当に全部かどうかに関係なく、「他には本当にないかな」と聞いてみましょう。それで少し考えるようなら、引き続き温かく見守ってあげてください。「本当に他にない」と主張するようになったら、「正解」なのか「まだある」のかを伝えてあげましょう。何度か繰り返しても全部あげきれない場合は、答えが何個あるのか、というヒントも出して構いません。
解いてみよう
Level 1
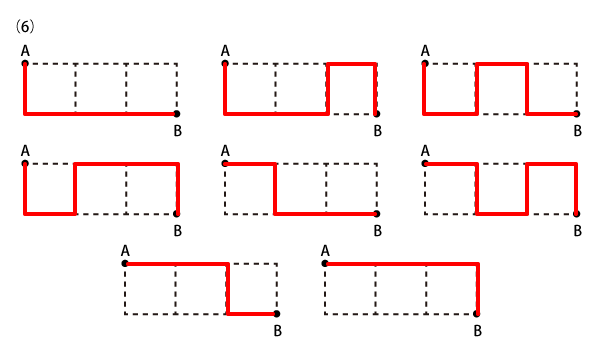
それぞれの図の点Aから点Bまで、点線にそって線を引くとき、線の引き方をすべて書いてみてください。ただし、同じ線や点を2回以上通ってはいけません。遠回りするのは構いません。
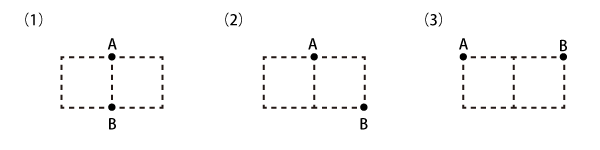
Level 2
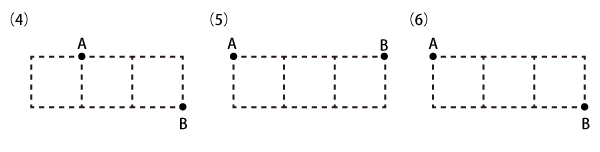
Level 3
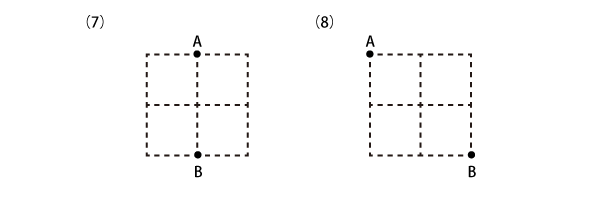
解答(例)
Level 1
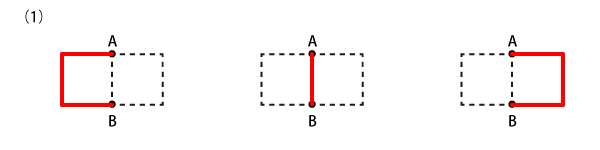
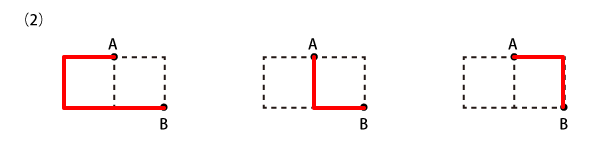

Level 2
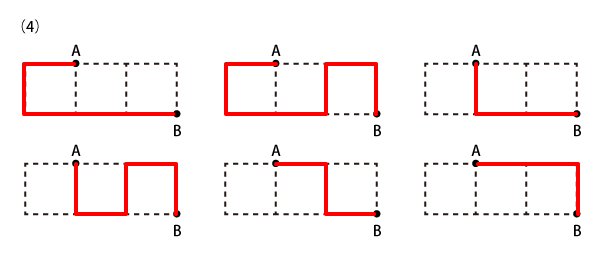
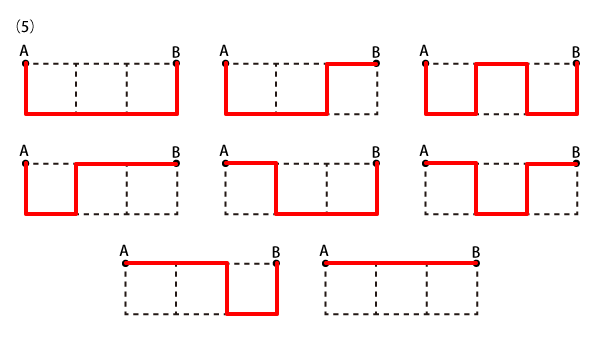
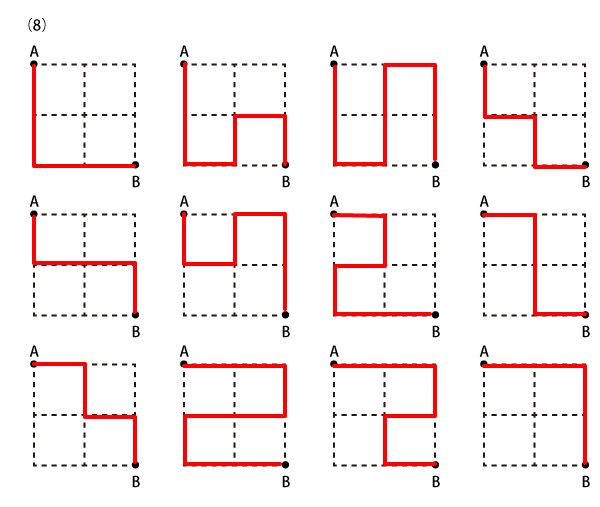
Level 3
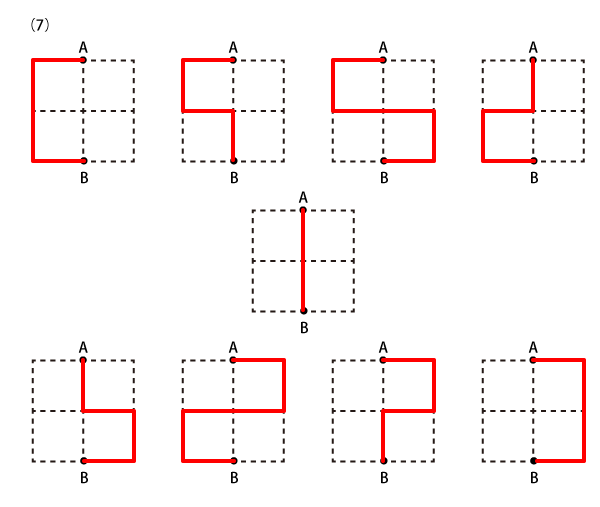
さんすう力UPのポイント
算数の学習を通して、論理的な思考力を身につけたい、と思う人も多いでしょう。しかし、その「論理的な思考力」とは実際にどういうものなのか、と聞かれると、結構あいまいなのではないでしょうか。実際、日常生活でいう「論理」と算数・数学の学習を進めるのに必要な「論理」では、少し意味合いが違います。算数以外の場面では、話のつながりに説得力があれば「論理的」と評価されることも多いでしょう。しかし、算数では多少説得力があったところで、それがそのまま「論理的」とされることはまずありません。算数の論理において大事なことは、「必ずそうなる」ということだからです。たとえば、「おなかがすいたからおやつを食べた」という文があったとしましょう。普通にとらえれば、別に不自然なところはない文章ですね。理由と結論の対応として問題はなく、「論理的」であるということはできますね。しかしこの文を「必ずそうなる(する)か」という視点から見るとどうでしょうか。別に、おなかがすいたからといって、必ずしもおやつを食べる必要はないわけです。おなかがすいても、何も食べずに晩御飯まで我慢をする、という選択肢はあります。そうやって、「おなかがすいても、必ずしもおやつを食べるわけではないよね」と考えていくのが、算数での「論理」なのです。
そういう話をすると、算数の「論理」ってあまり役に立たなさそうだね、と思うかもしれません。
しかしこれは逆で、役に立てようとするからこそ、「必ずそうなる」ことを考えなければならないのです。たとえば、算数の学習を進めていくと、「三角形の内角の和は180度である」というのを習いますよね。その事実を使って、「三角形ABCの角Aが40度で角Bが80度のとき、角Cは何度でしょう」みたいな問題を、「180-(40+80)=60度」というふうに解いていくわけです。ここで、「三角形の内角の和は、180度になることは多いが、たまに例外もある」と言われたらどうでしょうか。その例外がレアケースであったとしても、目の前の問題がその“例外”でないかどうかはわかりません。2つの角度が40度と80度だとわかっても、もしその三角形が「和が180度ではない三角形」だったとしたら、「60度」と答えると間違ってしまうことになります。そう考えると、「必ずそうなるとは限らない」では、あまり役に立たないのがわかりますか。さらに言えば、算数の問題を解くときには、ひとつ得た結論を、次の論理に使ったりもします。角度を順々に出していくときに、この「三角形の内角の和」を2回・3回と使っていくこともあるでしょう。その中に1つでも「180度にならない三角形」が混ざっていれば、正解にたどり着くことができないのです。やはり「必ずそうなる」ものでなければ、自信をもって「論理」を積み上げていくことができませんよね。
算数の論理では、「必ずそうなる」ことが大事です。算数での論理の運用能力を身につけるためには、まず「本当にそうなるか、それ以外の結論になることはないか」を考える姿勢を養うことが重要なのです。今回の問題のねらいは、その「他にもないか」を探してみるトレーニングを積むことです。正直に言えば、今回の問題はとても難しいです(特にレベル3は、自力で1回で全部あげきれれば、それは相当算数の力があると思っていいでしょう)。その意味では、今回の問題は「正解する」ことにあまり意識をおく必要はありません。それよりも、「他にもないか」と考えたり、実際に探してみて「他にないと思っていても意外と他にもある」という経験を積んでみたりすることができるよう、ぜひ温かく見守ってあげてください。
![]() そういえば、レジ袋、有料になってしまいましたね。個人的には、食品を直接カバンに入れるのは抵抗があるので、そういった買い物の際には引き続き有料でもレジ袋を利用することにしています。それ以外の買い物は、今までも比較的レジ袋をもらっていなかったので、そこまで変わらないような気がしますが、ひとつ困るのは「ちょっと近所のお店に買い物」という感じのときでしょう。先日、2Lの麦茶のペットボトルを買ったのですが、袋に入れるほどでないような気がして、結局コンビニから素手で持って帰りました。麦茶のペットボトルだけならまだいいですが、「飲み物+おにぎり2個」とかだと判断に迷いますよね。あまり買ったものを素手で持ち歩いていると、「家が近い」ということがわかってしまい、犯罪に巻き込まれる危険もあるということなので、なかなか難しいところはありますが、どの程度なら袋を使わず素手で持ち歩けるのか、またいろいろ挑戦してみたいと思います。
そういえば、レジ袋、有料になってしまいましたね。個人的には、食品を直接カバンに入れるのは抵抗があるので、そういった買い物の際には引き続き有料でもレジ袋を利用することにしています。それ以外の買い物は、今までも比較的レジ袋をもらっていなかったので、そこまで変わらないような気がしますが、ひとつ困るのは「ちょっと近所のお店に買い物」という感じのときでしょう。先日、2Lの麦茶のペットボトルを買ったのですが、袋に入れるほどでないような気がして、結局コンビニから素手で持って帰りました。麦茶のペットボトルだけならまだいいですが、「飲み物+おにぎり2個」とかだと判断に迷いますよね。あまり買ったものを素手で持ち歩いていると、「家が近い」ということがわかってしまい、犯罪に巻き込まれる危険もあるということなので、なかなか難しいところはありますが、どの程度なら袋を使わず素手で持ち歩けるのか、またいろいろ挑戦してみたいと思います。
それではまた来月!
| 文:小田 敏弘(おだ・としひろ)
数理学習研究所所長。灘中学・高等学校、東京大学教育学部総合教育科学科卒。子どものころから算数・数学が得意で、算数オリンピックなどで活躍。現在は、「多様な算数・数学の学習ニーズの奥に共通している“本質的な数理学習”」を追究し、それを提供すべく、幅広い活動を展開している(小学生から大人までを対象にした算数・数学指導、執筆活動、教材開発、問題作成など)。 公式サイト:http://kurotake.net/ 主な著書
|
















