小田先生のさんすう力UP教室
同じ数を足していこう
2020.9.24
7.5K


さんすう力を高めるにはどうしたらいいの? まあ、そんなに難しく考えないで、まずはお子さまと一緒に問題に取り組んでみましょうよ。
(執筆:小田敏弘先生/数理学習研究所所長)
![]() こんにちは、最近豚の角煮を作った小田です。実は引っ越す前に立派な圧力鍋を買っていたのですが、家に置く場所がなかったので職場に置いたままになっていました。引っ越してようやく持ち帰ることができたので、いろいろ作ってみているのですが、やはり圧力鍋って便利ですね。ある程度は下ごしらえもいりますが、基本的には材料を入れたらあとはあまりやることがないですからね。まあ、やることがないというか、何もできない、と言ったほうが正しいのかもしれませんが。煮込みすぎて崩れていても、途中で気づけませんからね。もちろん、そういう失敗もすでにやらかしていたりはします。もっといろいろ勉強しないといけません。
こんにちは、最近豚の角煮を作った小田です。実は引っ越す前に立派な圧力鍋を買っていたのですが、家に置く場所がなかったので職場に置いたままになっていました。引っ越してようやく持ち帰ることができたので、いろいろ作ってみているのですが、やはり圧力鍋って便利ですね。ある程度は下ごしらえもいりますが、基本的には材料を入れたらあとはあまりやることがないですからね。まあ、やることがないというか、何もできない、と言ったほうが正しいのかもしれませんが。煮込みすぎて崩れていても、途中で気づけませんからね。もちろん、そういう失敗もすでにやらかしていたりはします。もっといろいろ勉強しないといけません。
さて、今回の問題は数の迷路です。迷路なので、分岐や行き止まりはもちろんありますが、ルールとしては難しくないでしょう。まずはお気軽にチャレンジしてみてください。
それでは早速行ってみましょう。
Stage7:同じ数を足していこう
例題
<例題> 図のような迷路があります。スタートからゴールまで、通ったマスの数が2ずつ増えるように進んでください。
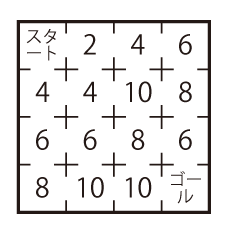
例題の答え
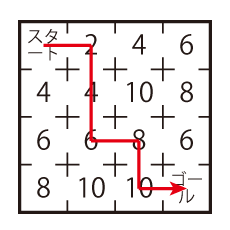
問題の意味は大丈夫でしょう。まずは温かく見守ってあげてください。行き止まりで手が止まってしまうようであれば、「迷路だから、行き止まりがあったり、道が分かれたりもあるよ」と伝えてあげてください。
ゴールにたどり着いたら、「答え」と照らし合わせるのではなく、お子さんの書いたルートに沿って、本当に2ずつ増えているかどうかを確認してあげましょう。ちゃんと2ずつ増えていて、ゴールまでたどり着いていたら正解です。途中で「2増えて」いないところがある場合は、「ここは違うね」と指摘してあげてください。
解いてみよう
Level 1
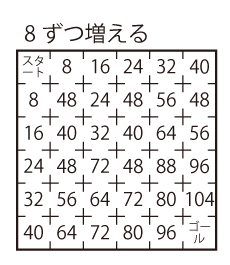
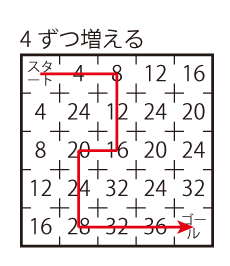
図のような迷路があります。スタートからゴールまで、通ったマスの数が決められた数ずつ増えるように進んでください。


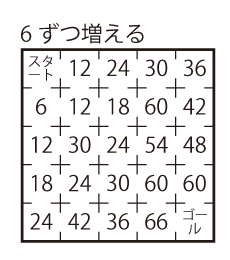
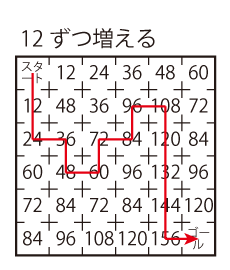
Level 2
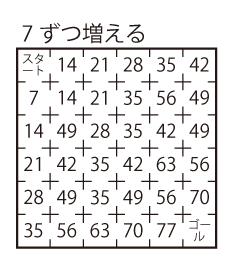
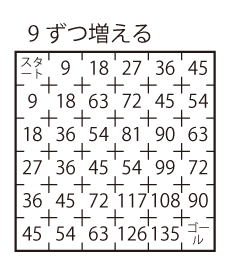
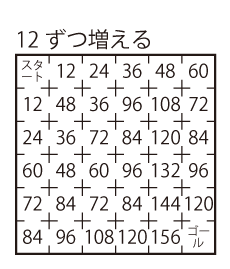
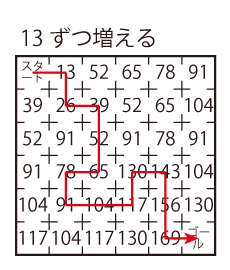
Level 3

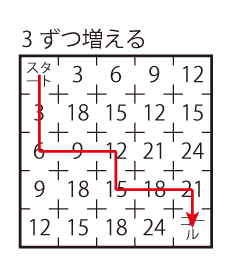
解答(例)
Level 1
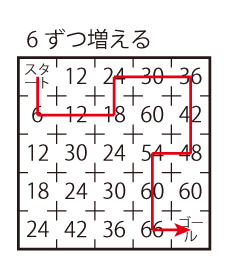
Level 2
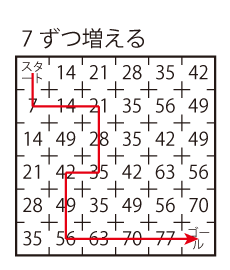
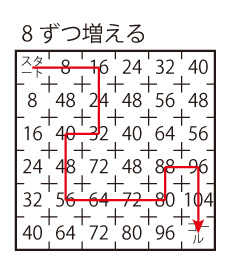
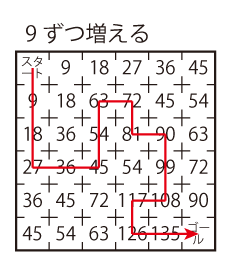
Level 3
さんすう力UPのポイント
7月号で、「計算力を身につけるには数と仲良くなることが大事だ」というお話をしましたね。数と仲良くなって数のいろいろな面を知り、“数”についての理解を深めていくことが、計算力を身につけるための基盤になる、という話でした。その「数についての理解」こそが、ある意味では「数のセンス」でもあるわけですが、その「数のセンス」を磨いていくためにぜひ取り組んでほしい問題の一つが、今回の問題です。
「足し算と掛け算の関係は、実はとても難しい」と言うと、驚きますか。「そんなの簡単じゃないか、掛け算は足し算をまとめたものだろう」と思う人もいるかもしれません。確かに、小学校で最初に掛け算を学習するときはそのように習いますね。しかし、スタートはそこであっても、さらにそこから数の世界を探検していくと、「掛け算の世界」というのはもっと奥が深く、「足し算をまとめたもの」という以外にも様々な面を持っていることに気づきます。
足し算の世界と掛け算の世界との一番大きな違いの一つは、その世界の構造でしょう。足し算の世界のイメージは、図1のように一直線につながった世界です。0または1をスタートにして、「1を足す」ごとに、その次の数、その次の数、……と進んでいく世界です。一方で、掛け算の世界のイメージは、図2のような枝分かれした世界です。図2では2と3の掛け算だけしか書いていませんが、いわゆる「素数」をスタートにして、そこにさらに「素数」を掛けていくと数が作られていくイメージです。(図2では、2を掛けると右上の数に進み、3を掛けると右下の数に進むようになっています。)
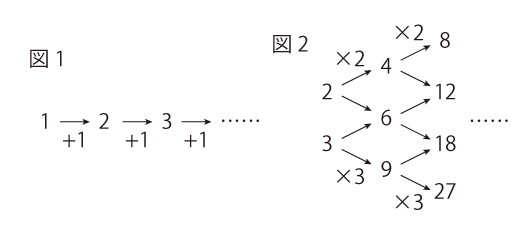 こうやって見てみると、同じ数の世界であっても、ずいぶん違ったものに見えませんか。“数”の世界を二つの違った構造でとらえる、というのは、“数”というものを複数の視点からとらえるということでもあります。複数の視点を持つことができれば、“数”への理解もさらに深まるでしょう。冒頭で、数のセンスを身につけるというのは数についての理解を深めることだ、という話をしましたが、こうやって二つの世界から数を見ることができるようになれば、それはまさに「数のセンス」に直結するのです。
こうやって見てみると、同じ数の世界であっても、ずいぶん違ったものに見えませんか。“数”の世界を二つの違った構造でとらえる、というのは、“数”というものを複数の視点からとらえるということでもあります。複数の視点を持つことができれば、“数”への理解もさらに深まるでしょう。冒頭で、数のセンスを身につけるというのは数についての理解を深めることだ、という話をしましたが、こうやって二つの世界から数を見ることができるようになれば、それはまさに「数のセンス」に直結するのです。
さて、この二つの世界を見えるようにする、つまり、「足し算の世界」だけでなく「掛け算の世界」も見えるようになるための入り口になるのが、「約数・倍数」という概念です。足し算の世界(図1)では、1からどの数にも進むことができますね。しかし、図2の掛け算の世界では、例えば2から27には直接進むことができません。スタートに選んだ数によって、「直接いける数」と「直接はいけない数」があるのです。「2から直接いける数」を「2の倍数」、「3から直接いける数」を「3の倍数」と言いますが、この「足し算の世界」にはない「倍数」のグループこそ、「掛け算の世界」を見るためのまず重要な手がかりなのです。その「倍数」のグループをなんとなく把握できるようにしよう、というのが、今回の問題の狙いです。
「2の倍数」からスタートして、「2ずつ足して」いけば、出てくるのは「2の倍数」ばかりです。「3の倍数」からスタートして、「3ずつ足して」いっても、出てくるのは「3の倍数」ばかりです。そうやって同じ数ずつ足していくのを繰り返すことで、そこに出てくる数同士をなんとなく「同じグループの数」と認識することが、「倍数」を見る目を養う第一歩です。
まだ「掛け算の世界」が見えていない子にとって、いきなり約数・倍数の概念をきちんと習得することは難しいでしょう。しかし、別に厳密に理解できなくても、ぼんやりとでも「この数字とこの数字は同じグループに入っている気がする」と思えるようになることは、その「掛け算の世界」を見るための重要なとっかかりにはなるはずです。今回の問題に取り組むことで、迷路を楽しみながら、ぜひそういった経験を積む機会を増やしていってほしいと思います。
![]() いかがでしょうか。
いかがでしょうか。
圧力鍋が使えるようになったり、使える食器が増えたりしたことで、少し自炊熱が高まってきている(私の中で)今日この頃ですが、最近「作った料理を保存する」という技術も覚えました。これまでの人生の中でも、自炊熱が高まった時期は何度かあったのですが、「作った料理を1回で全部食べる」というふうにしていたので、「結局、買ってきたほうが値段も量もちょうどいいじゃん」と思ってすぐブームが去っていったのです。しかし今回、作った料理を保存して何回かに分けて食べればいい、ということにようやく気付いたので、特に分量面で自炊を続けていくモチベーションが上がったかもしれません。できればこれを機に、おなか周りがもう少し落ち着くといいですよね。
それではまた来月!
| 文:小田 敏弘(おだ・としひろ)
数理学習研究所所長。灘中学・高等学校、東京大学教育学部総合教育科学科卒。子どものころから算数・数学が得意で、算数オリンピックなどで活躍。現在は、「多様な算数・数学の学習ニーズの奥に共通している“本質的な数理学習”」を追究し、それを提供すべく、幅広い活動を展開している(小学生から大人までを対象にした算数・数学指導、執筆活動、教材開発、問題作成など)。 公式サイト:http://kurotake.net/ 主な著書
|
















