小田先生のさんすう力UP教室
数字の構造をとらえよう
2020.12.24
5.8K


さんすう力を高めるにはどうしたらいいの? まあ、そんなに難しく考えないで、まずはお子さまと一緒に問題に取り組んでみましょうよ。
(執筆:小田敏弘先生/数理学習研究所所長)
![]() こんにちは、体がよく冷えるタイプの小田です。最近は、いろいろなところで体温を測られるようになりましたが、普段の体温より低く測られることが多いです。正直なところ、非接触型の体温計ってあんまりあてにならないな、と思っていたのですが、先日ついにサーモグラフィータイプの温度計で33度台をたたき出しました。きっと外気で体温(特に表面の温度)が下がりやすいのでしょうね。前世は爬虫類だったのかもしれません。冬眠する機能も引き継げればよかったのにな、と思う今日この頃です。
こんにちは、体がよく冷えるタイプの小田です。最近は、いろいろなところで体温を測られるようになりましたが、普段の体温より低く測られることが多いです。正直なところ、非接触型の体温計ってあんまりあてにならないな、と思っていたのですが、先日ついにサーモグラフィータイプの温度計で33度台をたたき出しました。きっと外気で体温(特に表面の温度)が下がりやすいのでしょうね。前世は爬虫類だったのかもしれません。冬眠する機能も引き継げればよかったのにな、と思う今日この頃です。
さて、今回は計算のパズルです。数字を入れて正しい式を完成させる、というシンプルなルールなので、気軽にチャレンジしてみてください。問題の構造上、複数答えが出ることもありますが、ひとつ答えていただければOKです。
それでは早速行ってみましょう。
Stage10:数字の構造をとらえよう
例題
<例題> 下の式の□に、4,6,9の数字をそれぞれ1回ずつ入れて、正しい式にしてください。
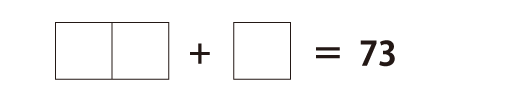
例題の答え
69+4など
今回は、問題の意味は大丈夫ですね。□が2つ並んでいるところは、2桁の数を表しています。4と6を順に入れた場合は「46」になる、という感じです。意味が大丈夫そうなら、あとは温かく見守ってあげてください。桁数の多い数の計算に慣れていない場合は、今回は無理に解かなくてもいいでしょう。数字の書かれたカードを用意してあげて、それを並べ替えるようにすると、「書いたり消したり」という作業がなくなるので、少し脳の負担が減って考えやすくなることもあります。
冒頭にも書いた通り、問題の構造上、正解が複数出る場合があるので、基本的にはお子さんの答えを実際に計算して正しければ正解、で構いません。計算してみて間違っていた場合は、実際の計算結果がいくつになるかを指摘してあげるといいでしょう。
解いてみよう
Level 1
下のそれぞれの式の□に、決められた数字をそれぞれ1回ずつ入れて、正しい式にしてください。
(1) 入れる数字:5,6,9
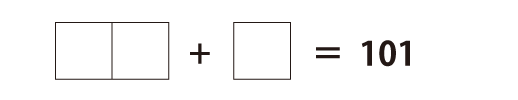
(2) 入れる数字:2,7,8
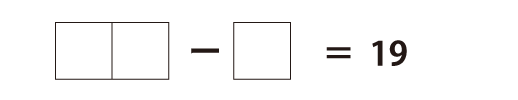
(3) 入れる数字:2,3,4,5

Level 2
下のそれぞれの式の□に、決められた数字をそれぞれ1回ずつ入れて、正しい式にしてください。
(4) 入れる数字:3,6,7,9

(5) 入れる数字:2,4,5,8

(6) 入れる数字:3,5,6,9

Level 3
下のそれぞれの式の□に、決められた数字をそれぞれ1回ずつ入れて、正しい式にしてください。
(7) 入れる数字:1,4,7,8,9
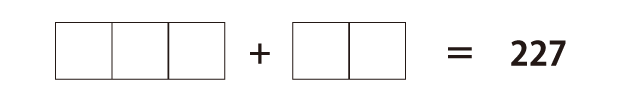
(8) 入れる数字:1,3,5,7,8,9

解答
Level 1
(1) 95+6など (2) 27-8 (3) 32+54など
Level 2
(4) 63+79など (5) 58-42 (6) 65-39
Level 3
(7) 148+79など (8) 351+897など
さんすう力UPのポイント
算数の学習を進めていく際、ハードルのひとつとして立ちはだかるのが「数の表し方」でしょう。大人になると、いつの間にか当たり前のように「1234」を「千二百三十四」と読むようになりますが、これは決して自然に身につくものではありません。
幼い子どもをよくよく見ていると、「数」の概念そのものは、実はある程度自然に身につけていることがわかります。たとえば、まだ言葉をしゃべることのできない段階でも、遊んでいるボールが5個から4個になると、残り1つを探そうとしたりするでしょう。しかしそうやって「4つ」と「5つ」の違いを感覚的に把握してはいても、「1」という記号を見て「1つ」と認識することは難しいでしょう。「1つ」という数を「1」という記号で表すことは、これはあくまで人類が決めた単なるお約束にすぎないからです。「そう読む」という知識なしに、自然に読めるようになるものではないのです。大人が数を読むのにそれほど苦労しないのは、経験を積んだことで、そのルールに慣れたからでしょう。逆に言えば、まだ「数字」という表記のシステムに馴染みのない子どもたちにとって、「数字」を読むことはそれなりに負担の大きいことなのです。
その「数字」というシステムの中でも、特に受け入れるまでに時間がかかる要素は、やはり「10進法」でしょう。たとえば「111」と書かれたとき、左端の「1」と中央の「1」と右端の「1」では、同じ「1」でも持っている意味が違います。左端の「1」は「百が1つ」あるという意味ですし、中央の「1」は「十が1つ」の「1」です。右端の「1」は「一が1つ」という意味ですね。もちろん、こうやって数字の書かれた場所によって意味が変わることには、大きなメリットがあります。そのメリットのひとつは、やはり限られた種類の記号で無限の数を表せるというところでしょう。本来、数は無限に存在します。その無限の数に対して個別に記号を割り当てていくと、その記号は無限の種類が必要になってしまいます。しかし数を書く場所によって意味を変えるシステムであれば、その「書く場所」つまり桁数を増やしていくことで、無限の数を表すことが可能になります。実際、現在使っている数字のシステムでは、0123456789というたった10種類の記号だけで、無限の数を表すことができていますよね。このいわゆる「位取り」のシステムは、人類にとってひとつの大きな発明なのです。
とはいえ、というよりも、むしろだからこそ、子どもにとってそのシステムは“自然に”受け入れられるものではないのです。「じゅう」と「いち」をあわせて「じゅういち」なのに、「101」と書かずに「11」と書く、というのは、言われてみれば“不自然”です。この違和感を飲み込んで、スムーズに「数字」のシステムを使いこなせるようになるためには、身もふたもない話をすれば“慣れる”しかないでしょう。
今回の問題は、計算のパズルを通して、その「数字」のシステムに慣れていってほしい、という意図があります。2桁以上の足し算や引き算は、「位ごとに足したり引いたりする」というのが計算の肝です。この「位ごとに計算する」という視点がないと、地道に数えていくしかありません。たとえば「5+3」を計算するときに、「5,6,7,8」と数えて「答えは8」とするような感じになりますが、これでは大きな数の計算はとても面倒で、実質的には不可能でしょう。「23+45」を計算するときは、「20と40で60、3と5で8、あわせて68」とやりたいわけです。今回の問題で試行錯誤していく中で、位ごとの数に注目して計算する視点に馴染んでいってもらえたらいいな、と思います。
![]() いかがでしょうか。
いかがでしょうか。
今年もいよいよ終わってしまいますね。やはり今年はバタバタした一年で、いつの間にか終わってしまった、という感覚の方も多いのではないでしょうか。私も実際そのひとりで、年の瀬に至った現在でも、今年何かを成し遂げた気はあまりしません。とはいえ、振り返ってみれば、引っ越しをしてみたり、オンラインでの指導を始めてみたりと、環境が変わった一年ではありました。まだまだ先行きの見えない状況ではありますが、今年の変化をまた新しい成果につなげられるよう、来年も頑張っていきたいと思います。
それではまた来月!
| 文:小田 敏弘(おだ・としひろ)
数理学習研究所所長。灘中学・高等学校、東京大学教育学部総合教育科学科卒。子どものころから算数・数学が得意で、算数オリンピックなどで活躍。現在は、「多様な算数・数学の学習ニーズの奥に共通している“本質的な数理学習”」を追究し、それを提供すべく、幅広い活動を展開している(小学生から大人までを対象にした算数・数学指導、執筆活動、教材開発、問題作成など)。 公式サイト:http://kurotake.net/ 主な著書
|
















