小田先生のさんすう力UP教室
角度に注目してみよう
2021.7.22
4.5K


さんすう力を高めるにはどうしたらいいの? まあ、そんなに難しく考えないで、まずはお子さまと一緒に問題に取り組んでみましょうよ。
(執筆:小田敏弘先生/数理学習研究所所長)
![]() こんにちは、七夕には「餃子をうまく焼けるようになりたい」とお願いした小田です。相変わらず餃子スープを定期的に作って食べる生活をしているのですが、やはりたまには焼いてみたくもなりますよね。しかし意を決して餃子を焼いてみても、フライパンに焦げ付いてしまい、なかなかうまく焼けません。ひとまず織姫様と彦星様にお願いしたので、そのうちうまく焼けるようになればいいなと思いました。
こんにちは、七夕には「餃子をうまく焼けるようになりたい」とお願いした小田です。相変わらず餃子スープを定期的に作って食べる生活をしているのですが、やはりたまには焼いてみたくもなりますよね。しかし意を決して餃子を焼いてみても、フライパンに焦げ付いてしまい、なかなかうまく焼けません。ひとまず織姫様と彦星様にお願いしたので、そのうちうまく焼けるようになればいいなと思いました。
さて、今回は図形の問題です。いくつかの扇形を組み合わせて、決められた扇形や円を作ってください。見た目だけでは難しい、ということでしたら、もちろん印刷して切り取り、実際に並べてみても構いません。
それでは早速行ってみましょう。
Stage17:角度に注目してみよう
例題
<例題> 図の(あ)から(え)のパネルのうち3つを使って、(A)の形を作ります。使わないパネルはどれでしょう。
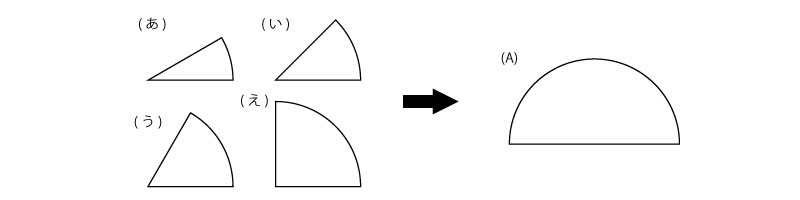
例題の答え
(い) たとえば、以下のように作ることができます。

【お詫びと訂正】
例題の解答に誤りがございました。使わないパネルは(う)ではなく(い)です。深くお詫びするとともに、上記の通り訂正させていただきます。
問題の意味は大丈夫ですね。4つの扇形のうち、3つを使って半円を作るだけです。問題としては「要らないものを答える」ようになっていますが、「答えたもの以外の3つでどうやれば作れるか」も聞いてみてください(もちろん、難しければ無理に答えさせなくても構いません)。
「どうやれば作れるか」はそれほど正確でなくても構いません。線を引いてもらって、どれがどれのつもりなのかを聞いてあげればいいでしょう。だいたい合っていれば正解にしてあげてください。大きくずれているように見えた場合は「もう少し大きい(or 小さい)」と伝えてあげてもいいでしょう。
慣れていない段階では、なかなか大きさをつかむのが難しいと思いますので、ぜひ印刷して切り取るなど、実物を用意してあげてください。
解いてみよう
レベル1
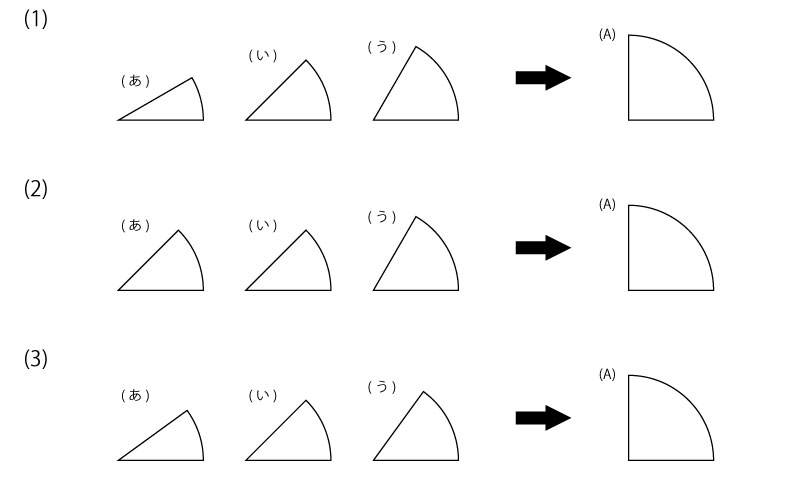
それぞれ、図の(あ)から(う)のパネルのうち2つを使って、(A)の形を作ります。使わないパネルはどれでしょう。
Level 2
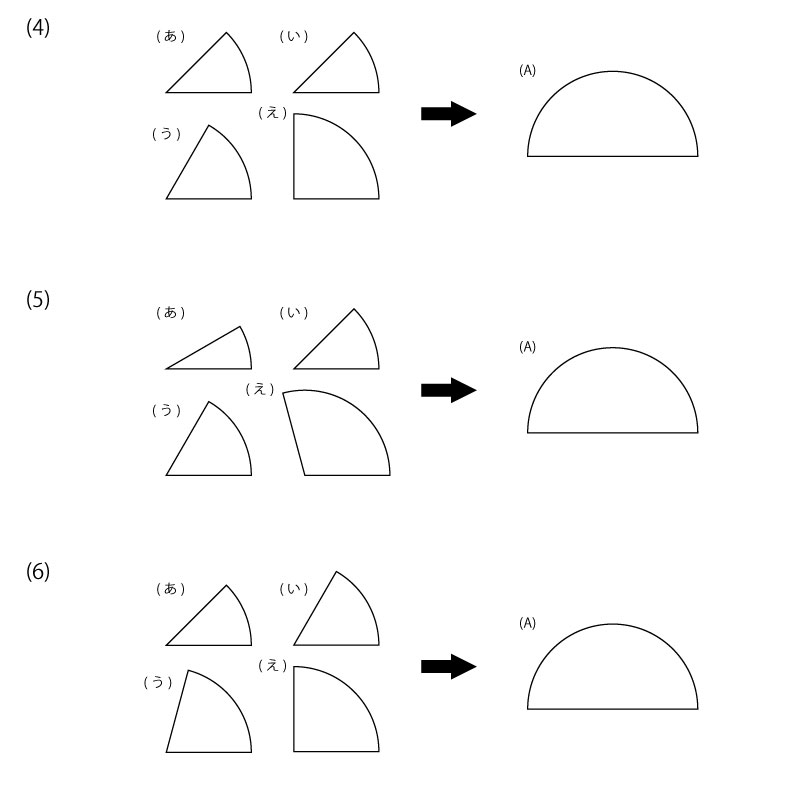
それぞれ、図の(あ)から(え)のパネルのうち3つを使って、(A)の形を作ります。使わないパネルはどれでしょう。
Level 3
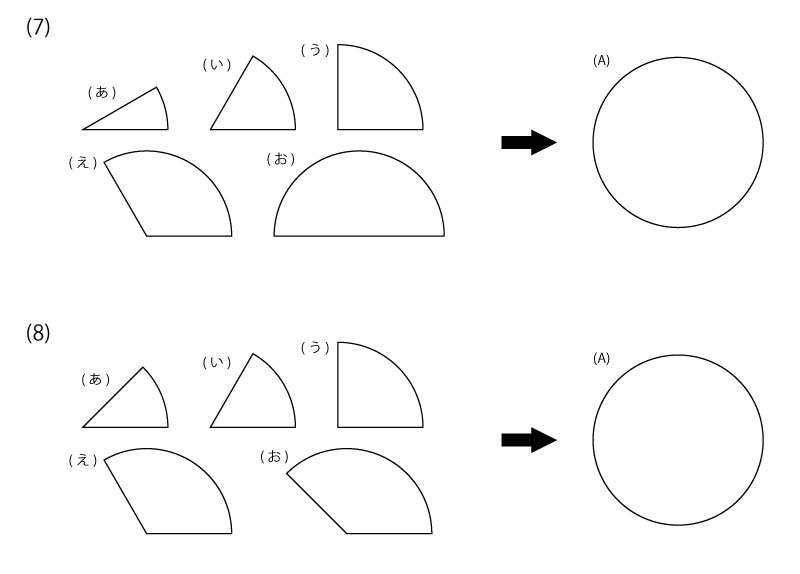
それぞれ、図の(あ)から(お)のパネルのうち4つを使って、(A)の形を作ります。使わないパネルはどれでしょう。
解答
Level 1
(1) (い) (2) (う) (3) (い)
※ それぞれ、たとえば以下のように作ることができます。

Level 2
(4) (う) (5) (う) (6) (え)
※ それぞれ、たとえば以下のように作ることができます。

Level 3
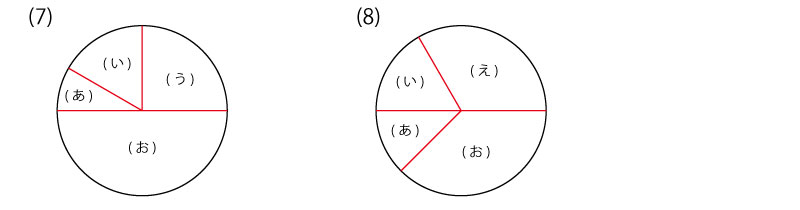
(7) (え) (8) (う)
※ それぞれ、たとえば以下のように作ることができます。
さんすう力UPのポイント
今回のテーマは、タイトルにもある通り「角度」についてです。たくさんの子どもたちを見ていると、角度という概念を理解するのは実は結構難しいことなんだな、と気付かされます。しかしそれは、子どもに限った話でもありません。「角度」とは何か説明してください、と言われたら、うまく説明できますか。
図形に関する量のことを「図形量」と言います。つまり、長さや面積、体積、そして角度のことですね。これらはいずれも、一言でいえば「大きさ」ということなのですが、どこに注目した「大きさ」なのかで呼ばれ方が違います。昨年度の2月号で、長さと面積の区別を獲得するのはひとつのハードルである、という話をしました。そちらでも書きましたが、算数の学習を進めていく前の段階では、これらのいろいろな種類の「大きさ」の区分はまだ分かれておらず、意識的にそれらの区別をするのは難しいでしょう。その違いを納得していくことこそが「算数の学習」なのですが、その中でも角度の概念を獲得するのは、とても大きなハードルのひとつであると感じます。
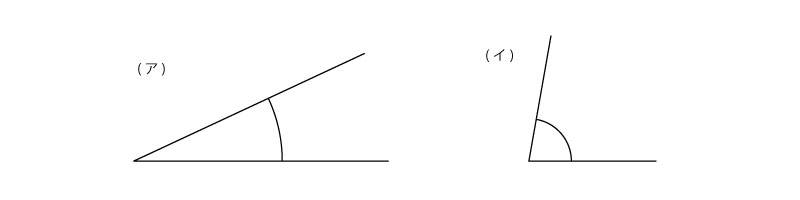
上の図で、どちらの方が角度が大きいですか、と聞くと、小学校高学年くらいでも「(ア)のほうが大きい」と答える子がそれなりにいます。それは、いわゆる「角度マークの大きさ(面積)」で、角度の大小を判断しているからでしょう。その状態の子は、まだ面積と角度の区分を獲得できていない、と言えますね。一般的な教科書や問題集では、角度マークの半径はだいたいどれもそろえて書かれているので、角度の大小を角度マークの面積で考えていても、それほど困らずに学習を進められてしまいます。しかしそれは逆に、角度の概念を獲得しないまま学習を進めていけてしまう、ということでもあるので、先々で急にわからなくなってしまうこともあるでしょう。今回の上の図ように、わざと角度マークの半径を変えて見せるのはある意味では意地悪をしているわけですが、こうやって角度の概念を他の図形量の概念から区分できているかを確認することも、どこかのタイミングでは必要です。
角度の概念の習得の難しさは、その「目に見えなさ」にあります。そもそも、角度とは何なのでしょうか。この質問には、いくつか答え方があると思います。代表的なもののうちのひとつは、「2本の線の開き具合」、もうひとつは「回転の量」です。

いずれにしても、角度は「具体的に目には見えない量」であることがわかりますか。角度マークをつければ「見える」ようにはなりますが、しかしそれは長さや面積へと間違って誘導されてしまう可能性もあります。長さや面積、体積といった他の図形量より、角度の概念の獲得がさらに難しい理由のひとつには、その「目に見えなさ」が大きく関係しているのでしょう。角度の概念をうまく獲得していくためには、やはりその目には見えない角度を「見る」経験が必要です。
今回の問題の狙いは、その「角度を見る」経験を積んでもらうところにあります。いくつかの「角度」を合わせたときに、(作りたい図形の)「角度」より大きいのか小さいのか。実際に並べてみたときに、隙間にどの「角度」がうまく入るのか。そういったことを試行錯誤していくうちに、特に今回はそれぞれの扇形の2本の半径の「開き具合」に注目できるようになるといいな、と思っています(その意味では、慣れないうちは実物を並べる経験を増やしてほしいところです)。
![]() いかがでしょうか。
いかがでしょうか。
今年もなかなか外に出づらい夏になりそうですね。そういえば、ちょうど昨年の夏に引っ越しをしたのでした。それまで自宅は「寝る場所」でしかなかったのですが、家にいる時間が増え、もう少し過ごしやすい広さが必要だなあ、と思ったからです。そんなこんなで引っ越してから1年が経過したわけですが、まだ半分以上段ボールが開いていない、というのはここだけの秘密です。1年使わなかったものは不要なものだ、と誰かが言っていたような気がしないでもないです。この夏は、部屋の片づけができればいいなと思います。
それではまた来月!
| 文:小田 敏弘(おだ・としひろ)
数理学習研究所所長。灘中学・高等学校、東京大学教育学部総合教育科学科卒。子どものころから算数・数学が得意で、算数オリンピックなどで活躍。現在は、「多様な算数・数学の学習ニーズの奥に共通している“本質的な数理学習”」を追究し、それを提供すべく、幅広い活動を展開している(小学生から大人までを対象にした算数・数学指導、執筆活動、教材開発、問題作成など)。 公式サイト:http://kurotake.net/ 主な著書
|
















