小田先生のさんすう力UP教室
円盤に色をぬってみよう
2021.8.26
8.9K


さんすう力を高めるにはどうしたらいいの? まあ、そんなに難しく考えないで、まずはお子さまと一緒に問題に取り組んでみましょうよ。
(執筆:小田敏弘先生/数理学習研究所所長)
![]() こんにちは、夏はそうめん率が高い小田です。先日、スーパーで「電子レンジでそうめんがゆでられるタッパー」を見つけました。レンジでパスタがゆでられるタッパーには常日頃お世話になっているので、こちらも買って使ってみたのですが、やはり便利ですね。湯切りはもちろん、水洗いもそのままできるという優れものです。実際にゆでるよりは少し時間がかかりますが、鍋を見ていなくてもいい、というのは大きなメリットですよね。こういったものを作ってしまえる人たちは、本当にすごいといつも思っています。
こんにちは、夏はそうめん率が高い小田です。先日、スーパーで「電子レンジでそうめんがゆでられるタッパー」を見つけました。レンジでパスタがゆでられるタッパーには常日頃お世話になっているので、こちらも買って使ってみたのですが、やはり便利ですね。湯切りはもちろん、水洗いもそのままできるという優れものです。実際にゆでるよりは少し時間がかかりますが、鍋を見ていなくてもいい、というのは大きなメリットですよね。こういったものを作ってしまえる人たちは、本当にすごいといつも思っています。
さて、今回は円盤に色をぬっていく問題です。同じような色の組み合わせでも、いろいろなパターンのぬり方がありますが、それらを全部並べてみよう、という問題です。すべて書き出すのはやってみるとなかなか難しいことに気づきますが、まずは気軽にチャレンジしてみてください。
それでは早速行ってみましょう。
Stage18:円盤に色をぬってみよう
例題
<例題> 図のような円盤に、赤、青、黄の3色をぬります。扇型のとなりあう場所は、同じ色でぬってはいけません。使わない色があってもいけません。同じ色を何回か使うのは構いません。回転させて同じになるぬり方は同じぬり方とするとき、考えられるぬり方をすべて答えてください。(全部で3通りあります。)

例題の答え

まずはいつも通り、問題の意味が理解できているかを確認してあげましょう。「それぞれのエリアに1色ずつ色をぬる」ということと「となりあうエリアを同じ色でぬらない」というのがわかっていれば、最初のうちは大丈夫です。「同じ色を使ってもいい」という条件は、聞かれたら問題文で確認してあげてください。「3色ともすべて使う」という条件や、「回転させて同じものになるものは同じ」というのは、探していく中で順次指摘してあげればいいでしょう。
正解かどうかを確認するときは,「2回ぬられている色が何色か」に注目するのがいいですね。4箇所に3色ぬるので、1色だけ2回、そのほかの色を1回ずつぬることになりますが、この「2回ぬる色」が決まれば残りの色のぬり方は1パターンずつしかありません(回転させると同じになります)。そこに注目して、同じものがあれば「これとこれは同じだよ」と伝えてあげてください。同じであることを確認するときには、時計回りに順番に「赤、青、赤、黄」と色を読み上げてあげるとわかりやすいでしょう。最初のうちは、どこに注目するのかお子さんには伝えなくても構いませんが、苦戦するようなら「2つぬる色から決めてごらん」と伝えてあげても大丈夫です。
解いてみよう
レベル1
それぞれ図のような円盤に、決められた色をぬります。となりあう場所は、同じ色でぬってはいけません。使わない色があってもいけません。同じ色を何回か使うのは構いません。回転させて同じになるぬり方は同じぬり方とするとき、考えられるぬり方をすべて答えてください。
(1) ぬる色:赤、青、黄、緑(6通りあります)

(2) ぬる色:赤、青、黄(6通りあります)

Level 2
(3) 図のような円盤に、赤、青、黄の3色をぬります。となりあう場所は、同じ色でぬってはいけません。使わない色があってもいけません。同じ色を何回か使うのは構いません。回転させて同じになるぬり方は同じぬり方とするとき、考えられるぬり方をすべて答えてください。(全部で11通りあります。)
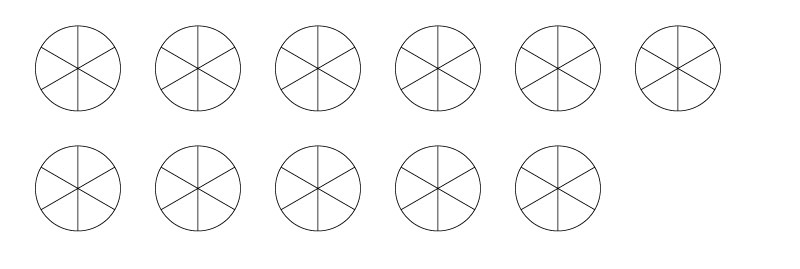
Level 3
(4) 図のような円盤に、赤、青、黄、緑の4色をぬります。となりあう場所は、同じ色でぬってはいけません。使わない色があってもいけません。同じ色を何回か使うのは構いません。回転させて同じになるぬり方は同じぬり方とするとき、考えられるぬり方をすべて答えてください。(全部で24通りあります。)

解答
Level 1
(1)

(2)

Level 2
(3)

Level 3
(4)
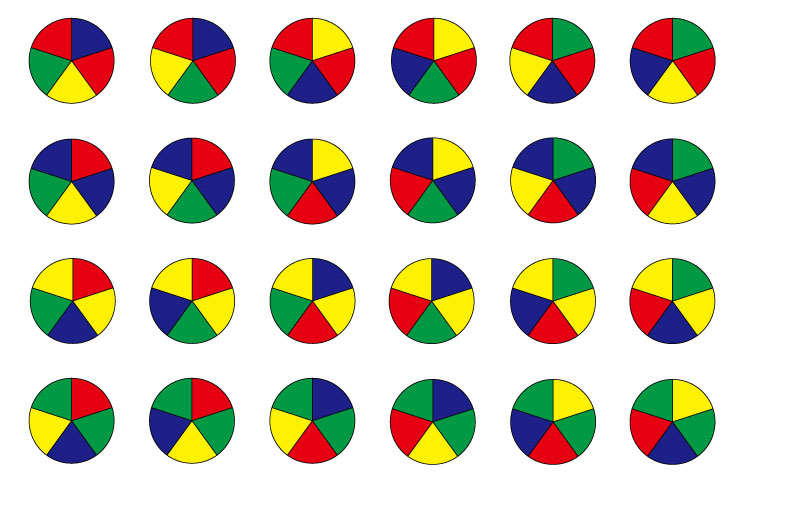
さんすう力UPのポイント
特に後半の問題を実際にやってみるとわかりますが、1回で全パターンを書き出すのはなかなか難しいですよね。しかしある意味では、こういった問題で「1回で正確にきちんと書き出せる力」こそ、算数における「論理の力」のひとつなのです。
算数の問題を正しく解いていくためには、「与えられた条件から考えられる候補」をもれなくダブりなく想定できることが大事です。たとえば、「AとBの2つの数があり、その合計が10」と言われたとき、「AもBも5だ!」と思ってしまうと、間違った結論にたどりつく危険性が高いでしょう。2つとも5の場合ももちろん合計は10になるのですが、それ以外にも「Aが2、Bが8」や「Aが0、Bが10」でも合計は10になりますね。「Aが3.5、Bが6.5」なんてこともあるかもしれません。そのうちのどれが正解なのかは、他の条件から考えていくことになるでしょう。算数の問題を解いていて間違えてしまうとき、こうした「思い込み」が原因になっていることが少なくありません。
思い込みで結論を決めつけず、「他の可能性もないかな」と考えられるようになるためには、まず「他の場合もないかどうか考えてみよう」という姿勢そのものが大事です。それはそれで身につけていくのは難しいのですが、それをようやく身につけたとしてもさらにその先、もう一段階「実際に候補を挙げていく力を身につける」というハードルがあります。
今回の問題で(特に後半の問題では)、実際に「他にないかな」と探してみても、なかなか最後の1つが見つけられなかったりするでしょう。見つけたと思っても、よくよく見ると、すでに書いたパターンだったりすることもあるはずです。この2段目のハードルの本質は、「技術」なので、練習して身につけていくしかありません。とはいえ、技術論ではあるので、いくつかのコツや注目するべき点はあります。
たとえば、「どこかに注目してグループを分ける」ことや「順に書いていく」ことなどがそれにあたります。例題の解説で、「2回ぬられている色に注目するといい」という話をしましたね。同じように、(2)でも複数回ぬられる色に注目するといいでしょう。3回ぬるとどう頑張ってもとなりあってしまうので、同じ色は2回までしかぬれません。しかし、2回ぬる色が1色だけだと3色で5つのエリアはぬれませんよね。3色で5つのエリアをぬるためには、「2色を2回ずつ使い、残りの1つを残った色でぬる」方法しかないのです。そこで、「赤と青を2回ずつ、黄を1回」「赤と黄を2回ずつ、青を1回」「青と黄を2回ずつ、赤を1回」という3つのグループに分けて調べていくと、見落としもずいぶん減るのではないでしょうか。(4)も同様に、「1色を2回ぬり、残り3色を1回ずつ使う」方法しかないので、これもやはり2回ぬる色に注目してグループ分けをするといいでしょう。(3)は少し難しいですが、「1色を3回、もう1色を2回、残り1色を1回使う」ときと「3色とも2回ずつ使う」ときとに分かれます。前者の方は「どの色を3回使うか」で分けて探すといいですね。後者の方は、赤をぬる場所に注目し、「1つ間をあけて赤をぬるとき」と「2つ間をあけて赤をぬるとき(つまり、赤を向かい合う位置にぬるとき)」でさらに分けると探しやすいかもしれません。
(1)は4色で4箇所ぬるので、同じ色は使えませんね。どれも1回ずつ使うことになるので、使う色で分けて探していくことができません。こちらは「順に書いていく」方法で探していくのがいいでしょう。これも例題の解説で少し触れましたが、たとえば(1)なら「赤をぬったところ」からスタートして時計回りに色を読み上げてみます。そのとき、「赤青黄緑」「赤青緑黄」「赤黄青緑」「赤黄緑青」「赤緑青黄」「赤緑黄青」というふうに、「赤→青→黄→緑」の順に優先順位をつけ、その順に変えていくと数えもらしを減らすことができます。(4)で2回使う色を決めたあとも同様です。たとえば赤を2回使うときは、残りを「青→黄→緑」のように順を決めて変化させていくといいでしょう(解答の並びも参考にしてみてください)。
今回のような問題が初めての場合、もちろんそこまでできる必要はありません。最初の段階では、「全部探し出すことの難しさ」を実感し、その難しさを楽しむことがまず大事です。そこから先、「もっと上手く探せるようになりたい」と思ったとき、技術的な方法論はきっと先に進むための道標になるでしょう。もちろん、いくつかアイディアを聞いたところで、それだけでいきなりうまく探せるようにはなりませんが、「工夫すれば複雑なことでもうまくできるようになるんだ」という実感を、少しずつ積んでいってもらえるといいな、と思います。
![]() いかがでしょうか。
いかがでしょうか。
実は最近冷蔵庫が壊れました。もちろん、冷凍室も使えません。正確に言うと、冷蔵室の調子が悪かったので、冷凍室の出力を下げれば冷蔵室の方に冷気がいってくれるかな、と思ったのですが、冷蔵室の出力が上がらないばかりか、冷凍室の出力も下がりっぱなしになりました。その結果、ストックしていた冷凍餃子が使う前に解凍されてしまったりもしました。悲しいですね。6月号くらいで「冷凍庫を買い足そう」みたいな話もしていましたが、それより先に冷蔵庫そのものを買い直すことになりそうです。まあ、ちょうどいいタイミングといえばそうなのかもしれませんが。冷蔵庫を買いなおした暁には、冷凍庫も駆使して自炊を増やしていきたいと思います!
それではまた来月!
| 文:小田 敏弘(おだ・としひろ)
数理学習研究所所長。灘中学・高等学校、東京大学教育学部総合教育科学科卒。子どものころから算数・数学が得意で、算数オリンピックなどで活躍。現在は、「多様な算数・数学の学習ニーズの奥に共通している“本質的な数理学習”」を追究し、それを提供すべく、幅広い活動を展開している(小学生から大人までを対象にした算数・数学指導、執筆活動、教材開発、問題作成など)。 公式サイト:http://kurotake.net/ 主な著書
|
















