小田先生のさんすう力UP教室
基本的な図形と仲良くなろう
2020.7.23
8K


さんすう力を高めるにはどうしたらいいの? まあ、そんなに難しく考えないで、まずはお子さまと一緒に問題に取り組んでみましょうよ。
(執筆:小田敏弘先生/数理学習研究所所長)
![]() こんにちは、近々引っ越す予定の小田です。今の住居も結構長く住んでいて気に入っていたのですが、先般の自粛期間中に家にいることが増え、落ち着いて過ごすには少し手狭だな、と思ったので引っ越すことにしました。よくよく考えると、住み始めたころとは生活スタイルも変わっているので、ちょうどいい機会かな、と思います。まあ、手狭なのは物を捨てないから、という説もあり、それも引越しの機会に頑張って断捨離していこうとは思っています。とりあえず、「何かに使えると思って取っておいた容器」類は、基本的には捨てていくつもりです。
こんにちは、近々引っ越す予定の小田です。今の住居も結構長く住んでいて気に入っていたのですが、先般の自粛期間中に家にいることが増え、落ち着いて過ごすには少し手狭だな、と思ったので引っ越すことにしました。よくよく考えると、住み始めたころとは生活スタイルも変わっているので、ちょうどいい機会かな、と思います。まあ、手狭なのは物を捨てないから、という説もあり、それも引越しの機会に頑張って断捨離していこうとは思っています。とりあえず、「何かに使えると思って取っておいた容器」類は、基本的には捨てていくつもりです。
さて、今回は図形の問題です。ルールは難しくないでしょう。いくつかのパネルを使って決められた形を作るパズルです。まずはぜひ、気軽にチャレンジしてみてください。
Stage5:基本的な図形と仲良くなろう
例題
(ア)の3つのパネルを使って、(イ)の形を作ってください。パネルは裏返したり、回転させたりして使っても構いません。

例題の答え(例)

問題の意味は大丈夫でしょう。
まずは、お子さんの好きなようにさせてあげてください。お子さんが定規を使いたがるようでなければ、最初はむしろフリーハンドで取り組ませてあげましょう。
正解は<例>以外にもありますので、ひとまず指定された形を使って問題の図ができていればOKです。線や形は、多少上手く描けていなくても、形同士の位置関係や大きさが合っていれば、正解にしてあげてください。
それぞれのパネルの大きさの関係が怪しい場合や、なかなか答えにたどりつけない場合、まずは定規を使うことを提案してあげてください。大きさをはかったり、まっすぐな線を定規で引いてみたりするといいよ、と伝えてあげるのです。
それでも難しい場合は、パネルを印刷して切り取り、実際に形を並べてみましょう。段階としては、まずパネルだけを並べて(作る形のほうは使わずに)やってみて、それでも無理なら作る形も印刷してその上に並べていく、という順序にするといいです。
解いてみよう
Level 1
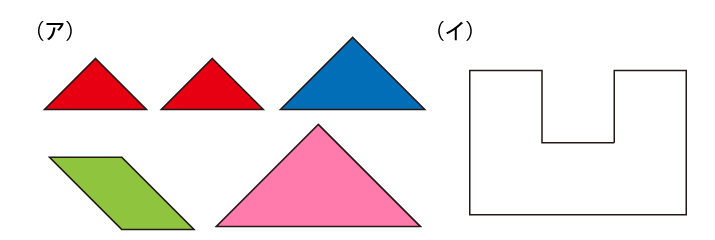
(ア)の3つのパネルを使って、(イ)の形を作ってください。パネルは裏返したり、回転させたりして使っても構いません。



Level 2
(ア)の4つのパネルを使って、(イ)の形を作ってください。パネルは裏返したり、回転させたりして使っても構いません。



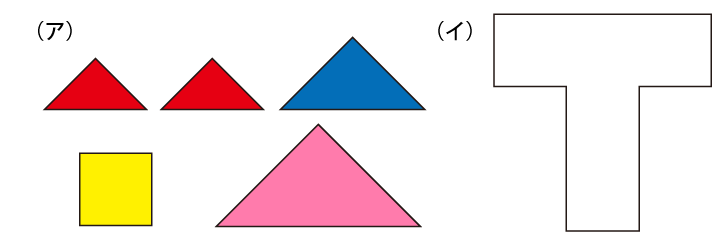
Level 3
(ア)の5つのパネルを使って、(イ)の形を作ってください。パネルは裏返したり、回転させたりして使っても構いません。

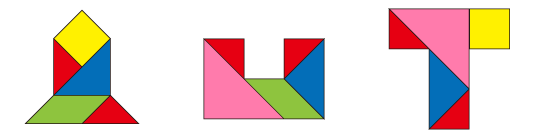
解答(例)
Level 1

Level 2

Level 3
さんすう力UPのポイント
5月号では、図形の学習において「センス」だけでなく「技術」も大事だという話をしましたが、今回は逆に、その「(図形の)センス」の中身を掘り下げていこうと思います。
ひとくちに図形のセンスと言っても、それを構成する要素はいろいろとあるのですが、その中でも重要なもののうちの1つは、やはり「基本的な図形」への理解でしょう。
算数の学習で登場する図形の中には、いくつか「基本的な図形」と呼べるものが存在します。シンプルではあるものの、組み合わせ方が多様で、まさに様々な図形の「基本」となる図形です。例をあげると、正方形や正三角形などがそういった図形にあたりますが、今回の問題のテーマになっている「直角二等辺三角形」も、その基本的な図形の1つと言えるでしょう。
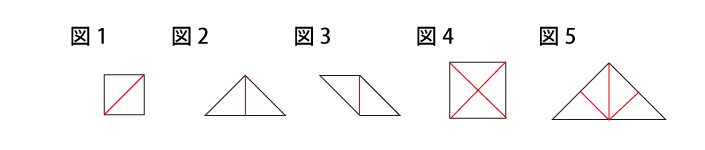
直角二等辺三角形は、「1つの角が直角で、その直角を挟む2つの辺の長さが等しい三角形」です。しかし、その“定義”を覚えただけでは、直角二等辺三角形を理解したことにはなりません。いろんな向きから眺めてみたり、実際に手に取って動かしてみたり、組み合わせて他の形を作ってみたりする中で、その図形のイメージを豊かにしていくことが、「直角二等辺三角形を理解する」ということだからです。たとえば、直角二等辺三角形を2つ組み合わせると、図1のような正方形になります。つまり、逆に言えば、直角二等辺三角形は正方形を半分にしたものでもあります。別の向きに2つくっつけると、図2のような、少し大きな直角二等辺三角形を作ることもできます。これも逆に言えば、直角二等辺三角形を半分にするとまた直角二等辺三角形になる、ということです。他に2枚でできる形には図3のような平行四辺形がありますが、これも問題のパネルに含まれていますね。2枚で正方形や直角二等辺三角形ができるということは、「2枚で作った直角二等辺三角形」を2つくっつけると、また正方形や直角二等辺三角形ができます (図4・図5)。なかなか面白いと思いませんか。
直角二等辺三角形のイメージを豊かにしていけば、それは必然的に90度や45度のような角度に対する理解にもつながります。組み合わせて同じ形を作れることから、相似(拡大・縮小)などのイメージを作っていくこともできるでしょう。また、枚数を考えることで、それらの面積の理解にもつながります。
形の名前や特徴を覚える、というのは、算数の学習の中ではとても重要な要素です。ただ、「勉強」という中で、言ってみればビジネスライクな関係でそれらの図形と付き合っていくだけでは、やはりその図形の一部の面だけしか見ることができず、理解を深めていくのもなかなか難しいでしょう。図形を理解するためには、図形と仲良くなることが大事です。ともに遊び、様々な面を見ることで、イメージが豊かになり、理解が深まるのです。今回の問題を通して、直角二等辺三角形とぜひ仲良くなってほしいと思います。
ちなみに、今回の問題で出てくるパネルは、いずれも「タングラム」のパーツの一部です。有名なのでご存じの方もいらっしゃると思いますが、「タングラム」は図6のように正方形を7つのパーツに切り分け、これらを使って様々な形を作る玩具です。いろいろな会社から商品化されていますので、興味のある人はぜひそちらも遊んでみてください。(単純な形なので、自作するのもありですね。)

![]() 今回、ちょうど図形の話なのでまた少し宣伝させていただきたいのですが、少し前に幻冬舎さんから発売された、『モンテプラス モンテッソーリ式 さいしょのずけいパズル』の問題監修をさせていただきました。問題作成のコンセプトは、まさに今回のテーマである、「基本的な図形と仲良くなる」というものです。対象は4~6歳なので、少しこちらの読者の方とはズレてしまうかもしれませんが、特に低学年でまだ図形に慣れていないお子さんにはぜひ遊んでみてほしいな、と思います。(もちろん、下に小さいお子さんがいらっしゃる方はぜひよろしくお願いします)。
今回、ちょうど図形の話なのでまた少し宣伝させていただきたいのですが、少し前に幻冬舎さんから発売された、『モンテプラス モンテッソーリ式 さいしょのずけいパズル』の問題監修をさせていただきました。問題作成のコンセプトは、まさに今回のテーマである、「基本的な図形と仲良くなる」というものです。対象は4~6歳なので、少しこちらの読者の方とはズレてしまうかもしれませんが、特に低学年でまだ図形に慣れていないお子さんにはぜひ遊んでみてほしいな、と思います。(もちろん、下に小さいお子さんがいらっしゃる方はぜひよろしくお願いします)。
それではまた来月!
| 文:小田 敏弘(おだ・としひろ)
数理学習研究所所長。灘中学・高等学校、東京大学教育学部総合教育科学科卒。子どものころから算数・数学が得意で、算数オリンピックなどで活躍。現在は、「多様な算数・数学の学習ニーズの奥に共通している“本質的な数理学習”」を追究し、それを提供すべく、幅広い活動を展開している(小学生から大人までを対象にした算数・数学指導、執筆活動、教材開発、問題作成など)。 公式サイト:http://kurotake.net/ 主な著書
|
















