小田先生のさんすう力UP教室
図形の大きさを考えよう
2021.1.28
7.4K


さんすう力を高めるにはどうしたらいいの? まあ、そんなに難しく考えないで、まずはお子さまと一緒に問題に取り組んでみましょうよ。
(執筆:小田敏弘先生/数理学習研究所所長)
![]() こんにちは、年始にはオンライン帰省した小田です。私の家と実家だけでなく、兄弟の家ともつないでテレビ電話的なことをしてみたのですが、意外とできてしまうものなんですね。住んでいる場所がばらけていると、なかなか会いに行くのが難しいご時世にはなっていましたが、久々にお互いの顔を見る・見せることができました。親も喜んでいたのでよかったです。
こんにちは、年始にはオンライン帰省した小田です。私の家と実家だけでなく、兄弟の家ともつないでテレビ電話的なことをしてみたのですが、意外とできてしまうものなんですね。住んでいる場所がばらけていると、なかなか会いに行くのが難しいご時世にはなっていましたが、久々にお互いの顔を見る・見せることができました。親も喜んでいたのでよかったです。
さて、今回は図形の問題です。「周りの長さ」を考える問題ですが、特にパズルになっているわけでもないので、素直に考えてもらって大丈夫です。まずは気軽にチャレンジしてみてください。
それでは早速行ってみましょう。
Stage11:図形の大きさを考えよう
例題
<例題> 下の3つの形の中で、周りの長さが1つだけ違うものがあります。それはどれでしょう。
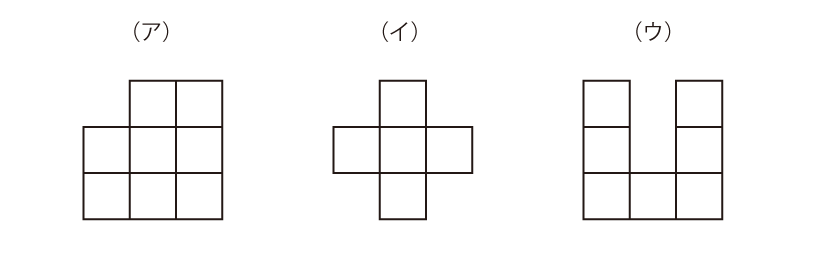
例題の答え
(ウ) それぞれ、周りの長さは、(ア):12、(イ):12、(ウ):16
まずは、問題の意味を理解できているかどうかの確認ですね。「周りの長さ」が何を指しているのかわかっていない様子でしたら、まずは図形の周をなぞりながら「ここの長さのことだよ」と伝えてあげてください。
感覚的に「これとこれと同じ」と答えるお子さんもいらっしゃると思いますが、それはそれで答えが合っていれば正解にして構いません。違う場合は「違うと思う」と伝えてあげればいいでしょう。お子さんに余裕があれば、「本当に同じなの?」と聞き返してみるのもいいですね。場合によっては「これこれこうだから、これとこれは同じ」というふうに説明してくれることもあるかもしれません。もちろん、「うん」とだけ返ってくるときもありますが、それはそれで大丈夫です。
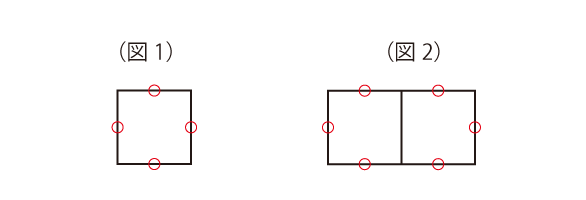
どこに注目していいかがわからない様子なら、図1、2のような例を挙げて、「図1だと4つ分、図2だと6つ分だね」と伝えてあげて構いません。
長さを数えて考えている場合は、長さを数え間違えたりしていたら、「数え間違えている」と伝えてあげましょう。
解いてみよう
Level 1
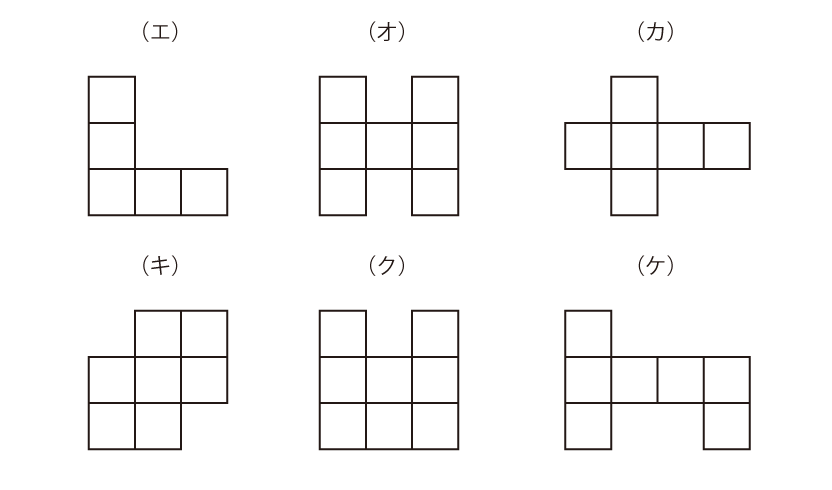
次の6つの形について、周りの長さが同じもの同士をペアにしてください。
Level 2
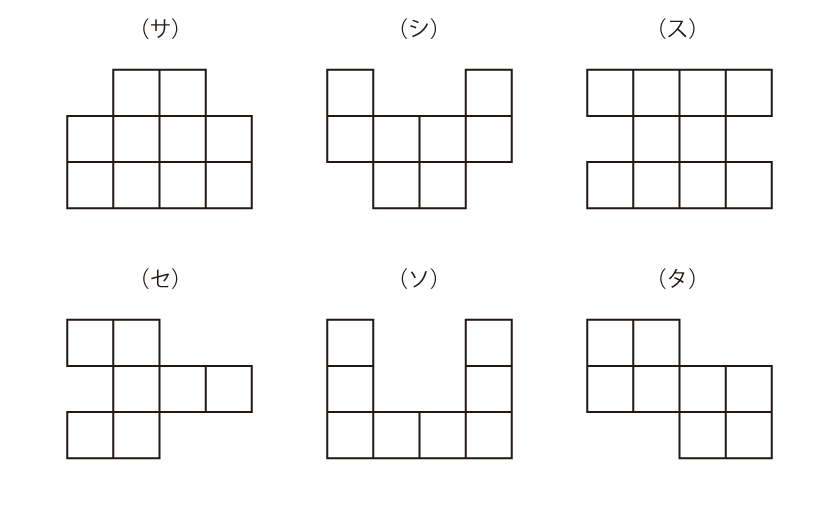
次の6つの形について、周りの長さが同じもの同士をペアにしてください。
Level 3
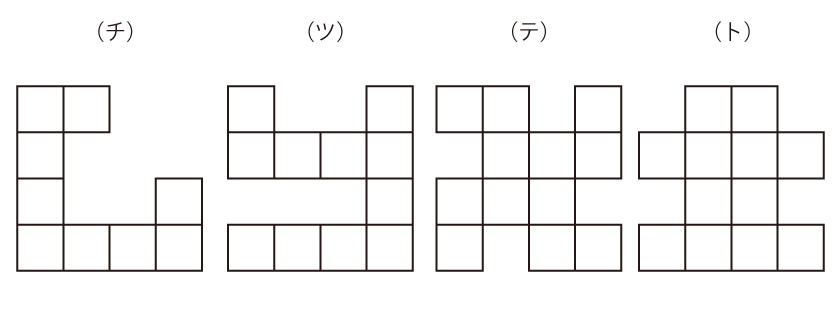
次の4つの形について、周りの長さが同じもの同士をペアにしてください。
解答
Level 1
(エ)と(キ)(長さ12)、(オ)と(ケ)(長さ16)、(カ)と(ク)(長さ14)
Level 2
(サ)と(タ)(長さ14)、(シ)と(セ)(長さ16)、(ス)と(ソ)(長さ18)
Level 3
(チ)と(ト)(長さ20)、(ツ)と(テ)(長さ24)
さんすう力UPのポイント
下の図3、図4を見せて「どちらのほうが大きいですか」と聞くと、「同じ」と答えてしまう子が一定数います。そういった子たちの考えていることをよくよく聞いてみると、ひとつ面白いことが見えてきます。
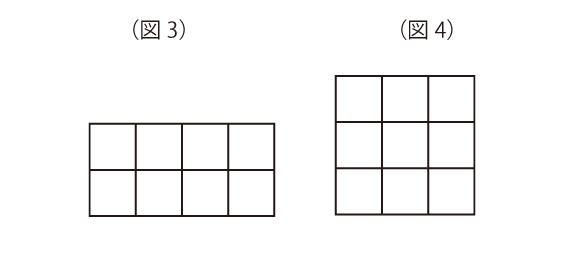
そもそも、「大きさ」とは何でしょうか。例えば、「図5の2つの扇形のうち、どちらが”大きい”か」と聞かれたらどう答えますか。少し答えに困ってしまうのではないでしょうか。
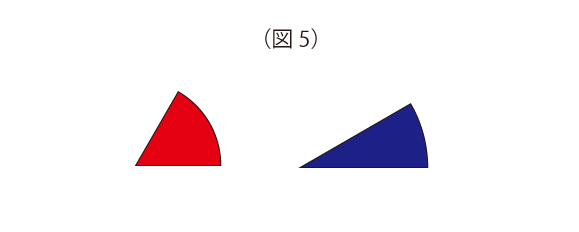
半径の“長さ”という意味では青い扇形のほうが“大きい”ですし、中心角(“角度”)は赤の扇型のほうが“大きい”ですね。“面積”で言えば、これは見た目では少し判断しづらいでしょう。こうやってよくよく考えると、「大きさ」という言葉にはいろいろな意味があることに気づきます。そう理解すると、図3と図4で「大きさが同じ」と答えてしまう子は、「周りの長さで大きさを考えているのだ」とわかります。周りの長さを考えると、図3も図4も12の長さだからです。
算数をなぜ学ぶか、という疑問は、特に算数が苦手な人にとっては切実な思いですよね。正直に言えば、この質問が「なぜ算数を学ばなければいけないか」という意図であれば、別に“学ばなければいけない”理由なんてないだろう、というのが私の意見です。しかし、「算数を学ぶとどういいことがあるか」という意図の疑問であれば、それにはいくつかの答えを提示することができるでしょう。そのひとつが、「算数を学習すれば、世界がより鮮明に、豊かに見えてくる」ということです。
たとえば、今回のテーマである「大きさ」はまさに典型的な例です。上で述べた通り、ひとくちに「大きさ」と言っても、その指すものにはいくつかの種類があります。具体的には、「角度」「長さ」「面積」それから「体積」です。その違いがあいまいな段階で「世界」を見ると、なんとなく「大きさ」を判断してしまい、場合によっては「大きいと思って選んだものが実は小さかった」ということも起こりうるでしょう。算数の学習を通して、大きさにもいろいろな種類があることを理解できれば、それらの区別に注意して世界を見ることもできるようになります。ケーキをたくさん食べたいときには体積に注目したり、色をぬるのに必要な絵の具の量を考えるときには面積に注目したり、カバンや箱に物が入るかどうかを知りたいときには長さに注目したり。そうやって、世界を詳細に見ることができる“目”を養うことが、算数を学習するメリットのひとつなのです。
今回の問題は、「長さ」に注目する問題です。しかし長さだけに注目してはいても、「周りの長さが同じなのに、広さ(面積)が全く違う図形」が見えてくることでしょう。まずは感覚的でもいいので、その“違い”に引っ掛かりを覚えてほしい、というのが今回の問題の狙いです。もちろん、すぐにその違いを理解してほしいということではありません。「周りの長さが同じもの」と問題文に書いてありますが、「マス目の数(面積)」を数えようとする子もいるでしょう。それはダメなことではありません。単にまだ長さと面積の区別があいまいな段階にいる、というだけであって、むしろこれからその切り分けができるように算数の学習を進めていけばいい、ということです。今回の問題が、その一歩になればいいな、と思いますので、周りのオトナの皆さんには、「子どもってそうなんだ」とぜひ面白がっていただきつつ、温かく見守ってあげてください。余談ですが、ちょうど先日別の雑誌のインタビューで、「算数の問題文って読むの難しいよね」という話をしました。それは、こういった「概念(ここでは長さと面積の区別)」を理解していないと「読めない」からです。そこで取り違えてしまう子は、別に「読み間違えた」わけではないのです。そういうお子さんには「問題を読みなさい」というのではなく、「長さ」っていうのはここのことだよ、と優しく伝えてあげてください。
![]() いかがでしょうか。
いかがでしょうか。
いよいよ受験シーズンが始まりました。私も今年は大学受験生、高校受験生、中学受験生をそれぞれみていますが、例年よりは意外と落ち着いた日々を過ごしています。それぞれが、やるべきことに自分できちんと向き合っている、ということなのでしょうね。昨年は大変な一年で、さらに未だに各方面で混乱が続く中、ここまで勉強を続けてきた受験生たちには、本当に頭が下がります。これは今年に限らず例年思うことではあるのですが、今年は特に、どういう結果に終わってもその過程で得たものは大きいはずなので、それをこれからの人生に活かしていってほしいな、と思います。
それではまた来月!
| 文:小田 敏弘(おだ・としひろ)
数理学習研究所所長。灘中学・高等学校、東京大学教育学部総合教育科学科卒。子どものころから算数・数学が得意で、算数オリンピックなどで活躍。現在は、「多様な算数・数学の学習ニーズの奥に共通している“本質的な数理学習”」を追究し、それを提供すべく、幅広い活動を展開している(小学生から大人までを対象にした算数・数学指導、執筆活動、教材開発、問題作成など)。 公式サイト:http://kurotake.net/ 主な著書
|
















