こんにちは、最近ネット通販にハマっている小田です。今までも、大手の通販サイトは利用していたのですが、本や文房具以外はあまり買ったことがありませんでした。最近は寒い日も増えてきて、外に出るのも億劫になってきたので、ネットで買えるものはなるべくネットで買うことにしたのです。ひとまず服を買ってみたのですが、服はサイズ選びで結構悩みますよね。手持ちの服と同じショップで同じサイズのものを買ってみたのですが、うまく行ったようなのでよかったです。通販サイトにはサイズを判定してくれるものもあるようなので、今度はそちらも使ってみたいと思います。
　さて、今回は仲間外れを探す問題です。今回は、一応「想定している解答」はもちろんあるのですが、自分なりに“他の形との違い”を説明できれば、どれを選んでも正解です。ぜひ気軽にチャレンジしてみてください。

　それでは早速行ってみましょう。

次の(ア)(イ)(ウ)の形のうち、仲間外れはどれでしょう。理由も答えてください。

（ウ）　中の記号がぬられていないから

問題の意味は大丈夫ですね。「仲間外れ」という言葉にピンとこないようでしたら、「他の図形と違う、と思うのはどれ？」と聞いてあげてください。
冒頭にも書いた通り、基本的に何を選んでも正解です。どれを選んだ場合であっても、「なぜ、それが仲間外れだと思う？」と聞いてあげてください。子どもなりに何らかの理由を見つけられていれば、それでOKです。大人から見ると、「それは本当に仲間外れかな？」と思うような答えであっても、「違いを見出した」ことそのものが大事ですので、ぜひ正解にしてあげてください。
ちなみに、この例題の場合でしたら、「（ア）だけ青が使われていない」「（イ）だけ緑が使われていない」「（ウ）だけ赤が使われていない」なども考えられますね。

（1）次の(ア)(イ)(ウ)の形のうち、仲間外れはどれでしょう。理由も答えてください。

（2）次の(ア)(イ)(ウ)の形のうち、仲間外れはどれでしょう。理由も答えてください。

（3）次の(ア)(イ)(ウ)の形のうち、仲間外れはどれでしょう。理由も答えてください。

（4）次の(ア)(イ)(ウ)の形のうち、仲間外れはどれでしょう。理由も答えてください。

（5）次の(ア)(イ)(ウ)の形のうち、仲間外れはどれでしょう。理由も答えてください。

（6）次の(ア)(イ)(ウ)の形のうち、仲間外れはどれでしょう。理由も答えてください。

（7）次の（ア）（イ）（ウ）（エ）の形のうち、仲間外れはどれでしょう。理由も答えてください。

（8）次の(ア)(イ)(ウ)の形のうち、仲間外れはどれでしょう。理由も答えてください。

※以下は，いずれも答えの例です。
（1）（イ）だけ外側の図形が丸。
（2）（ア）だけ外側の枠が縦長。
（3）（イ）だけ内側の図形が二重になっている。

※以下は，いずれも答えの例です。
（4）（ア）だけ内側の図形が上にある。
（5）（ウ）だけ外側の図形の線が細い。
（6）（ウ）だけ「丸と三角」ではない。

※以下は，いずれも答えの例です。
（7）（エ）だけ赤が使われていない。
（8）（イ）だけ外側と内側の図形が同じ色。

算数を学ぶ目的のひとつに、「異なるものの間に共通性を見つけ出す」「よく似たものの中に違いを見つけ出す」ことができるようになる、というものがあります。
たとえば、次の図形を見てください。この中で「台形」はどれでしょうか。「台形」はいくつかありますが、すべて選ぶことはできますか。

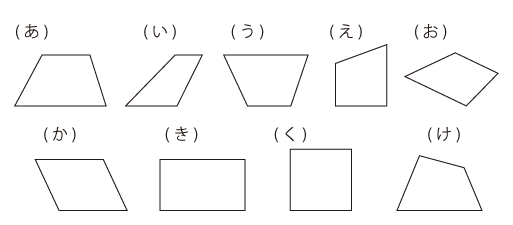
先に答えを言ってしまうと、実は（け）の形だけが「台形ではない形」で、そのほかはすべて「台形」です。（く）は「正方形」じゃないの、と思うかもしれませんが、正方形も台形の一種です。
台形かどうかを判断するためには、まず「台形とは何か」、つまり、台形の定義を確認する必要がありますね。台形とは、「向かい合う2組の辺のうち、少なくとも1組が平行である四角形」のことです。この定義にあてはまればすべて台形であり、あてはまらなければ台形ではない、ということです。（い）のように傾きが急であっても台形ですし、（う）のように上の辺の方が下の辺より長くても台形です。（え）は左の辺と右の辺が平行なので台形ですし、（お）も右上の辺と左下の辺が平行なので台形です。（か）（き）（く）はもちろんそれぞれ「平行四辺形」「長方形」「正方形」ですが、いずれも「少なくとも1組の辺が平行」という条件は満たしているので、台形の一種です（2組とも平行ですが、“少なくとも1組”という条件にはあてはまります）。
「台形」という語感に引きずられて「台のような形」と考えてしまうと、違った結果になるかもしれません。たとえば、（い）は実際に台として使うと、倒れてしまいそうですよね。逆に、（け）の方が、上の面が少し斜めになっていますが、下の方は安定しており、「台」としては使えそうです。

算数の学習を進めていくと、いろいろな定義を学びます。中には、感覚的にはなかなか納得しづらい「定義」も出てくることもあり、なぜこんなものを覚えないといけないんだろう、と思うこともあるかもしれません。しかしもちろん、そういった「定義」を学ぶことには重要な意義があります。それは、「その定義にあてはまるものは、すべて同じように扱うことができる」からです。
たとえば、「台形」の定義にあてはまる形は、すべて「台形の面積の公式」で面積を求めることができます。台形の「向かい合う平行な辺」のうちの片方を「上底」、もう片方を「下底」と呼ぶとすると、その「上底の長さと下底の長さを足した値」に「高さ（上底と下底の間の距離）」をかけて2で割ると、面積が出ます。式で書くと、「（上底＋下底）×高さ÷2」ですね（この式は、見たことがあるかもしれません）。台形の定義にあてはまる形、つまり上記の（あ）から（く）の形は、（上底、下底、高さを正しく選べば）この公式で面積を求めることができるのです。ここで、見た目が「台」の形に見えるかどうかは、関係ありません。むしろ、「台の形」に近い気がする（け）の形は、上の辺の長さと下の辺の長さを足して“高さ”をかけて2で割っても、面積を求めることはできないでしょう。見た目ではなく、性質に注目した分類が、ここでは必要になりますね。算数で学ぶ様々な定義は、このグループ分けの“視点”を身につける、という意味があるのです。
「定義をする」というのは、共通部分を見つけ出して、それを言語化するということです。今回の問題は、その練習ですね。もちろん、今回の問題では“数学的な”分類を求めているわけではありません。まずは、「異なって見えるものの中に、共通点を見つけ出し、それにあてはまるものとあてはまらないものを考えてみる」という経験を積んでほしいのです。だからこそ、どれを選べば正解ということではなく、もっと気軽に、自分なりの視点で、「定義する」ことを楽しんでほしいと思います。

　いかがでしょうか。先月話題に挙げていた“レモンジュース”ですが、あれも結局、ネット通販で買いました。おかげさまで、心温まる日々を送っています（笑）。飲み物の類は、通販の方が便利ですよね。実際に買いに行くと、重くてまとめ買いが難しいですしね。ただ、牛乳や生鮮食品は、まだ通販で買うのは躊躇っているところです。牛乳はそもそもまとめ買いには向かないと思いますが、肉や野菜は冷凍保存できるので、通販でまとめ買いできると楽なんですけどね。またいろいろ調べてみようと思います。

　それではまた来月！