どーんとこい!中学入試の算数
第35回 「動かして考える」平面図形の問題
2019.11.28
12.8K



大人でもちょっと手こずってしまうような、難問奇問が続出する中学入試の算数。
でもだいじょうぶ、コツさえつかめば怖くありません!
学習サポートセンターのカズが、算数を楽しく学ぶ方法を伝授します。
今回は市川中学校の入試問題の類題です。中学校以降で習う平面図形の問題では、補助線を引いて考えることが多く、「図形を別の場所に動かす」という作業になじみのない保護者の方も多いかもしれません。しかし、「動かして考える」のがポイントとなる出題は、中学受験の算数ではたびたび見られます。「動かして考える」ことを知らずに解こうとすると、解き方をひらめくことはなかなか難しく、時間ばかり消費してしまうかもしれません。難関校をめざす方はぜひここでマスターしておきましょう。
問題
図のようなAB=AD、BD=CD、角ABCが120°である四角形ABCDがあり、点EをBCとEDが垂直となるようにBC上にとると、AEの長さが6cmになりました。アとイの角度をそれぞれ角BAE、角BCDとするとき、次の問いに答えなさい。

(1)イの角度がアの角度の5倍の大きさになるとき、アの角度を求めなさい。
(2)四角形ABEDの面積を求めなさい。
|
ヒント (1)BD=CDから、三角形DBCは二等辺三角形です。したがって、角DBCがわかれば角イも同じ角度になります。 (2)三角形ABEを動かして考えてみましょう。 (参考) |
解答・解説はこちら
解答
(1)
AB=AD、角BADは直角ですから、三角形ABDは直角二等辺三角形です。したがって、角ABDは45°です。よって、角ABCが120°だから、120-45=75により、角DBCは75°になります。
次に、三角形DBCに着目すると、BD=CDから三角形DBCは二等辺三角形です。よって、角DBCと角イは等しく75°になります。角イが角アの5倍の大きさであることから、角アは75÷5=15より
15° (答)
となります。
(2)
四角形ABEDにおいて、角BADと角BEDはともに直角だから、角ABEと角ADEをあわせた角度は180°になります。したがって、三角形ABEを図のように移動すると、
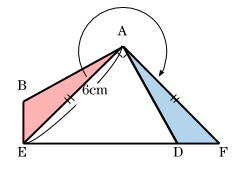
三角形AEFは直角二等辺三角形です。よって、この面積を求めればよいので、
6×6÷2=18
より、四角形ABEDの面積は
18cm2 (答)
冒頭でお伝えしたように、「動かして考える」問題の解き方を初見でひらめくのは、なかなか難しいものです。このように、「知っていれば解けるけれど、知らないと解くのはかなり厳しい」という問題は、本番の入試でもたびたび出題されます。試験で難しい問題に出合ったときは、少し考えてみて試行錯誤できそう(手を動かすことができそう)であればそのままチャレンジしてもよいですが、「何をしたらよいのかわからない」状態になったときには、その問題は捨てて次の問題に進む、と決めておくとよいでしょう。
さて、このコーナーは次回12月26日の更新が最終回になります。最終回は、中学受験で頻出の「その年の西暦」を利用した問題をいくつか出題します。中学受験では、「その年の西暦」に限らず、和暦や日付など、何かに関連した数字をどこかに使った出題がよく見られます。出題者の遊び心なのでしょうが、気がつけると楽しいですよね。
それでは、また来月お会いしましょう。
「さぽナビ」中学受験コース向け記事 アンケート
本アンケートは、「さぽナビ」中学受験コース向け記事において、より充実した情報提供のために役立てさせていただきます。
ぜひ、中学受験コースを受講している皆さまの声をお聞かせください。
まだZ会員ではない方
プロフィール
出題・文
学習サポートセンター カズ
Z会の学習サポートセンターで、日夜会員のみなさんからの質問相談に応じている。
















