まずはここをチェック!
最短でお届けできる申込締切日は
Z会プログラミングシリーズの特長
学習指導のプロである
Z会のカリキュラムで
誰もが得意になれる
-

興味を持って取り組める
日常生活とリンクした学習テーマを設定し、誰もが楽しみながら理解できるよう工夫されたZ会独自の教材と各種プログラミングツールを使って学びます。

日常生活とリンクした学習テーマを設定し、誰もが楽しみながら理解できるよう工夫されたZ会独自の教材と各種プログラミングツールを使って学びます。
-

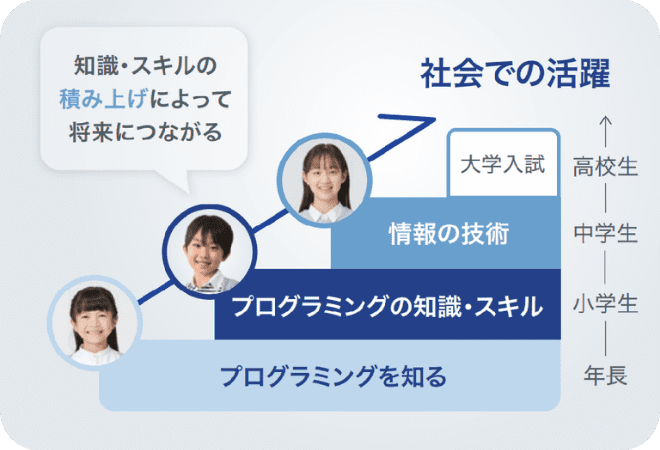
初歩から体系的に身につく
Z会の体系立てられたカリキュラムで、初歩から段階的に無理なく力を伸ばしていけます。
Z会の体系立てられたカリキュラムで、初歩から段階的に無理なく力を伸ばしていけます。
-

充実の保護者サポート
保護者の方向けの学習アドバイスをお届けしているので、お子さまと一緒にプログラミングを楽しむことができ、保護者の方がプログラミングになじみがなくても安心です。

プログラミングに楽しく取り組みながら、確実に力を身につける「定着プロセス」を組み込んだ学習サイクルでしっかり知識・スキルが身につきます。
Z会プログラミングシリーズ 講座一覧
学年・お子さまに合わせて
講座を選べます
推奨学年以外の方もご受講いただけます。
キャンペーン実施中
「プログラミングってなに?」がわかる
プログラミングはじめてみる講座
「プログラミングってどんなもの?」「ちょっと試してみたい」そんな声にお応えした3カ月講座。プログラミングが初めてのお子さまでも取り組みやすく、保護者の方へのサポートも万全です。
◯推奨学年
年長~小学2年生
◯こんな方におすすめ
- ●「プログラミングってなに?」が知りたい
- ●気軽にプログラミングにふれてみたい
- ●初めてなので手頃な価格・短期間で始めたい

「プログラミングってどんなもの?」「ちょっと試してみたい」そんな声にお応えした3カ月講座。プログラミングが初めてのお子さまでも取り組みやすく、保護者の方へのサポートも万全です。
◯推奨学年
年長~小学2年生
◯こんな方におすすめ
- ●「プログラミングってなに?」が知りたい
- ●気軽にプログラミングにふれてみたい
- ●初めてなので手頃な価格・短期間で始めたい
キャンペーン実施中
プログラミング学習を通じて
「みらい創造力」を身につける
プログラミングみらい講座 with KOOV®
小学生に必要なプログラミングの力をしっかりと身につけながら、自由制作や課題解決に取り組むことで、未来をひらくために必要な力を養っていきます。
◯推奨学年
小学1~4年生
◯こんな方におすすめ
- ●楽しくプログラミングを始めたい
- ●体系的・段階的なカリキュラムでプログラミングを
しっかり学びたい - ●試行錯誤しやすく扱いやすいブロックでプログラミングに
集中したい

小学生に必要なプログラミングの力をしっかりと身につけながら、自由制作や課題解決に取り組むことで、未来をひらくために必要な力を養っていきます。
◯推奨学年
小学1~4年生
◯こんな方におすすめ
- ●楽しくプログラミングを始めたい
- ●体系的・段階的なカリキュラムでプログラミングをしっかり学びたい
- ●試行錯誤しやすく扱いやすいブロックでプログラミングに集中したい
キャンペーン実施中
将来必須で、大学入試にもつながる
「情報活用能力」を身につける
Z会プログラミング中学技術活用力講座
最先端のプログラミングアプリで学ぶ3カ月の講座と、Raspberry Pi 400を使ってさまざまなソフトウェアを実践する12カ月の講座をご用意。どちらも充実のテキストが学びをナビゲートします。
◯推奨学年
- ●教科実践編
小学校高学年~中学3年生 - ●コンピュータ活用編
小学校高学年~中学3年生
◯こんな方におすすめ
- ●将来の大学入試に備えたい
- ●内申点対策をしたい
- ●将来社会で活躍できる力をつけたい

最先端のプログラミングアプリで学ぶ3カ月の講座と、Raspberry Pi 400を使ってさまざまなソフトウェアを実践する12カ月の講座をご用意。どちらも充実のテキストが学びをナビゲートします。
◯推奨学年
- ●教科実践編
小学校高学年~中学3年生 - ●コンピュータ活用編
小学校高学年~中学3年生
◯こんな方におすすめ
- ●将来の大学入試に備えたい
- ●内申点対策をしたい
- ●将来社会で活躍できる力をつけたい
通信教育のメリット
自宅で学ぶからこそ
-
教室のような
制限時間はありません。教室の場合はどんなに楽しくても、自宅には持ち帰れませんが、自宅学習ならお子さまが好きなときにじっくり取り組むことが可能です。
-
自宅の遊び時間を有効活用、
送り迎えも不要です。行き帰りの時間もなく、決まった曜日・時間に合わせる必要もないので、時間を有効に使って学習することができます。
-
キットが自分のものになるから
衛生面でも安心・安全です。通信教育なら、キットは共有ではなく自分のものになるので、衛生面でも安心・安全。また、受講修了後もキットやアプリはお使いいただくことが可能です。
-
お子さまの成長の過程を
見守ることができます。作品の実物を保護者の方に見せて共有できるのも自宅学習の魅力です。保護者の方の「すごいね」の一言が、お子さまの次のやる気につながります。
利用者の声
はじめたお子さまから
変わり始めています
-
プログラミングに興味を持ち始めた。休憩を忘れてしまうくらい、学習に夢中になっていた。
「プログラミングはじめてみる講座」利用者の声
-
自分で工夫してチャレンジを繰り返す中で、発想力や創造力が広がり、論理的な思考ができるようになってきたなと感じます。
「プログラミングみらい講座 with KOOV®」利用者の声
-
宿題などが終わったあと、一人で取り組んでいました。自分で組んだプログラムがうまく行ったことが楽しかったようで、何度も失敗しながらも集中して取り組んでいました。
「Z会プログラミング中学技術活用力講座 教科実践編」利用者の声
紙の資料でご検討されたい方には
お子さまの学年に応じた
パンフレットをお送りします

よくあるご質問
FAQ
- プログラミングを通信教育で学ぶメリットって?
- 自分専用のキットやタブレットでご自宅で安心して受講できることに加えて、お子さまが自分のペースで取り組めるので、好きなだけ思う存分、集中してぐんぐん力がつきます。学校の宿題や他の習いごとなどとの時間の調整がとりやすいのも通信教育とメリットと言えるでしょう。
- 教室とどちらが良いか迷っています。
- 教室と異なり、決まった曜日・時間に合わせる必要がなく、保護者の方が送り迎えをする必要もないので、時間を有効に使える点が大きなメリットです。また、教室だとお子さまの習得状況や成長を知る機会が限られてしまいますが、通信教育だと作品の実物をおうちの方に見せて共有できるのも通信教育の魅力です。
- 学校の授業だけでは不十分なの?
- プログラミング学習は、学校によってどれくらい取り組むかに差があり、十分な時間をとって身につくところまで学習できるとは限らないのが現状です。差をつけるためにも、校外学習をやっておくとアドバンテージになります。
- プログラミングを通信教育で学ぶメリットって?
- 自分専用のキットやタブレットでご自宅で安心して受講できることに加えて、お子さまが自分のペースで取り組めるので、好きなだけ思う存分、集中してぐんぐん力がつきます。学校の宿題や他の習いごとなどとの時間の調整がとりやすいのも通信教育とメリットと言えるでしょう。
- 教室とどちらが良いか迷っています。
- 教室と異なり、決まった曜日・時間に合わせる必要がなく、保護者の方が送り迎えをする必要もないので、時間を有効に使える点が大きなメリットです。また、教室だとお子さまの習得状況や成長を知る機会が限られてしまいますが、通信教育だと作品の実物をおうちの方に見せて共有できるのも通信教育の魅力です。
- 学校の授業だけでは不十分なの?
- プログラミング学習は、学校によってどれくらい取り組むかに差があり、十分な時間をとって身につくところまで学習できるとは限らないのが現状です。差をつけるためにも、校外学習をやっておくとアドバンテージになります。
Information


将来社会で活躍する人になるために
プログラミング学習を通して身につく「論理的に考え、試行錯誤して目的を達成する力」は将来の社会において、子どもたちが自分の夢を実現し、活躍していくための大きな力になります。
理系の人向けと思われがちなプログラミング学習ですが、実は「IT知識」や「プログラミングスキル」だけでなく、様々な課題を解決するための「情報活用能力」という、これからの時代に生きるすべての子どもに必要な力を得られる学びなのです。
プログラミング学習を通して身につく「論理的に考え、試行錯誤して目的を達成する力」は将来の社会において、お子さまが自分の夢を実現し、活躍していくための大きな力になります。
Z会プログラミングシリーズで、新しい学びをはじめましょう
Z会プログラミングシリーズで、
新しい学びをはじめましょう
SNSアカウント
Z会プログラミングシリーズ<公式>( @zkaiprogramming )
「Z会プログラミングシリーズ」のお得なキャンペーンや新商品の情報、近況などをお知らせします。◎こちらからご覧ください。
Z会プログラミングシリーズ<公式>( zkai_programming )
「Z会プログラミングシリーズ」のお得なキャンペーンや新商品の情報、近況などを画像や動画でお知らせします。◎こちらからご覧ください。
Z会プログラミングシリーズ
「Z会プログラミングシリーズ」のお得なキャンペーンや新商品の情報などをお知らせします。◎こちらからご覧ください。
Z会の通信教育
「Z会の通信教育」についてお得なキャンペーンや教育情報をお届けします。◎こちらからご覧ください。
※講座の名称や教材の仕様、価格等は変更になる可能性がございます。
※本サイトでは、「プログラミングはじめてみる講座」を「はじめてみる講座」、「プログラミングみらい講座 with KOOV®」を「みらい講座」と表記している場合があります。また、®やTMなどのマークを省略している場合があります。
Apple、Apple のロゴ、Mac OS、iPad、Safari は、米国および他の国々で登録されたApple Inc. の商標です。
「Z会プログラミング講座 みらい with ソニー・グローバルエデュケーション」、「プログラミングみらい講座 with KOOV®」および「Z会プログラミング中学技術活用力講座」は、株式会社Z会と株式会社ソニー・グローバルエデュケーションの協業による講座です。
KOOV®およびPROC® は 、株式会社ソニー・グローバルエデュケーションの登録商標です。
「Z会プログラミング中学技術活用力講座」で使用している商標等については以下のWebサイトをご覧ください。
https://www.zkai.co.jp/z-programming/jr/license
【Amazonギフトカード(Z会プログラミングシリーズ ご友人・ごきょうだい紹介制度)について】
本キャンペーンは株式会社Z会による提供です。本キャンペーンについてのお問い合わせはAmazonではお受けしておりません。Z会プログラミング事務局までお願いいたします。
Amazon、Amazon.co.jpおよびそれらのロゴはAmazon.com, Inc.またはその関連会社の商標です。
















