こんにちは、ゴールデンウィークは半分くらい寝ていた小田です。しっかり休んでしっかり遊ぼうと思っていたのですが、新年度であふれた仕事を片付けたり、体力を回復したりしていたら、いつの間にか終わってしまっていました。一応、帰省したりそのついでに少し出かけたりはできたので、それはそれでよかったとは思いますが。欲を言えば、部屋の掃除などもしたかったのですが、それはまた日々少しずつやっていこうと思います。

さて今回は、「すべて答える」問題です。候補をもらさないようにすべて挙げるのは、算数の学習の中ではとても大事なことなのですが、結構難しかったりもします。まずはその難しさを楽しんでみてください。

それでは早速行ってみましょう。

 

Stage63：ほかにもないか探してみよう

例題

○の書かれたカードが2枚、×の書かれたカードが2枚、合計4枚のカードがあります。この4枚のカードを1列に並べるとき、並べる順番として考えられるものを、すべて答えてください。

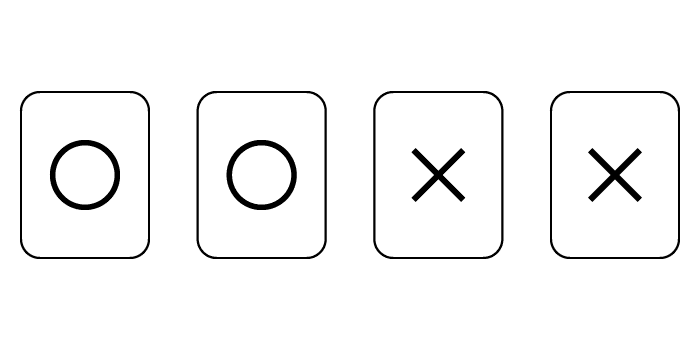
例題の答え

○○××，○×○×，○××○，×○○×，×○×○，××○○（全部で6通り）

まずは問題の意味が理解できているかを確認してあげましょう。いまいちピンときていないようなら、1つか2つくらいは具体例を伝えてあげてもかまいません。頭の中でイメージするのが難しければ、実際に紙を切って“カード”を作ってみるのもいいでしょう。「縦に並べる」「横に並べる」といった“並べ方”ではなく、あくまで“並べる順番”を考える問題なので、そのあたりで引っ掛かっている場合は、それも確認してあげてください。

問題の意味がわかったようなら、あとは温かく見守りましょう。お子さまが、「これで全部」としたら、まずは「条件に当てはまっていないもの」がないかどうか、確認してあげてください（たとえば、○の数や×の数があわないものなど）。その次に、「同じものを2回以上書いていないか」も確認します。それらが特になければ、「足りないものがないか」を確認してあげましょう。足りないものがあるときは、「まだあるよ」とだけ伝えてあげれば大丈夫です。「あと何個あるか」は、最初のうちは伝えなくていいでしょう。お子さまの様子を見ながら、心が折れそうになったら「あと○個だよ」と教えてあげてもかまいません。

 

レベル１・２・３の問題に挑戦！

難度別に3段階の問題を掲載しています。ぜひ、親子で挑戦してみてくださいね。

▲画像クリックで拡大します（PDFファイル）
 

解答を確認しよう！

解答はこちら 
 

さんすう力UPのポイント

「これからは正解のない時代だ」というようなことが言われ始めてから、それなりの月日が経ちましたね。教育界隈でも、「正解のない時代に向けての教育」みたいなことが、当たり前のように言われるようになってきました。そういうふうに言われるようになったのは、おそらくは「画一的な教育」に対する反発だとは思いますし、方向性としておおむね賛成ではあるのですが、ただ、“正解”というものがある意味で「画一的なもの」として扱われることには、個人的に少し違和感があったりはします。
　
算数の問題を解くというのは、本来は「問題で設定された条件を満たすものを探す」ということです。出題者がうまくいくつかの条件を重ねて、答えが「ただ1つ」に定まるようにしてある問題が多いですが、少なくとも「出題者の中にある“正解”」を“あてる”という性質のものではないのです。
　
条件の数を減らしたとき、その「条件を満たすもの」が1つであるとは限りません。問題を解いている途中で、一つひとつの条件を考えているときも同じですね。この条件を満たすものはこれとこれだが、そのうちこっちの条件も満たすものはこれ、という感じに絞っていくのが、算数の問題での「考える」という作業です。最初の段階で、“正解”を1つにしぼりこんでしまい、それがほかの条件にはあわないものだった場合、答えにたどりつくことができなくなってしまうでしょう。
　
算数の学習を進めていく中で、そういった「これしかない」という思い込みから脱していくことも重要です。今回のような問題は、そのためのトレーニングでもあります。何も考えずに見つけたものから並べていくだけでは、条件が複雑になると（枚数や種類が増えると）すべてあげ切るのは難しいでしょう。そのためには技術が必要で、その技術を身につけることも算数の学習の中で必要になってきますが、まずはその前段階として、「自分ではほかにもうないと思っていたけれども、実際にはほかにもあった」という経験を積んでほしい、というのが今回の問題の主な狙いです。
　
これからの時代にあっても、人生を生きていく中で、何か超えたいハードル、クリアしたい目標はいろいろと出てくるでしょう。その「条件」を満たすことが「正解する」ことであり、その意味では「正解すること」は、これからの時代も求められ続けるはずです。もちろん、その「正解」の条件が多様化したり、自分で設定する必要があったりすることは、否定しません。そういった方面の訓練も、それはそれで必要ではあるでしょう。しかし、だからと言って「正解する」トレーニングが不要というわけではありません。ゴールとなる「条件」と真摯に向き合い、思い込みで「これしかない」と断定することなく、慎重に「正解」を目指す力を、ぜひ磨いていってほしいと思います。

 

---

いかがでしょうか。

新年度、いろいろバタバタした結果、エアロバイクをあまりこいでいない今日この頃です。体重も、急激に増えたということはないのですが、以前よりも2〜3kgほど増えたところで安定中です。エアロバイクをやり始める前もそんな感じだったので、やはり真面目に運動しないといけないな、と思い始めてはいるところです。これから暑くなってきて寝づらくもなり、体力の回復にも気をつけないといけませんが、頑張りたいと思います。

それではまた来月！

 

「小田先生のさんすう力UP教室」の記事一覧はこちら