こんにちは、例のゲーム機を無事入手した小田です。もうずいぶん手に入れやすくなってきているので、頑張ればもっと早く入手できたかと思いますが、いろいろ面倒だったので公式の招待販売を待ちました。「届いたらやろう」と思っていたゲームがいろいろとあるのですが、この時期なかなかゲームをやる時間もとれず、悩ましいところです。年末年始にはのんびり遊びたいと思います。

さて今回は、数を分けていく問題です。もちろん、根本的には掛け算や割り算の話ではあるのですが、それらをまだ学習していないお子さまにも（むしろ、そういったお子さまにこそ）ぜひチャレンジしてもらいたいと思います。

それではさっそく行ってみましょう。

 

Stage70：同じ数ずつ分けてみよう

例題

6個のアメを何人かで同じ数ずつ分けます。あまりが出ないのは、何人で分けたときですか。考えられる人数をすべて答えてください。答えは4つあります。「1人のとき」も答えに入れていいものとします。

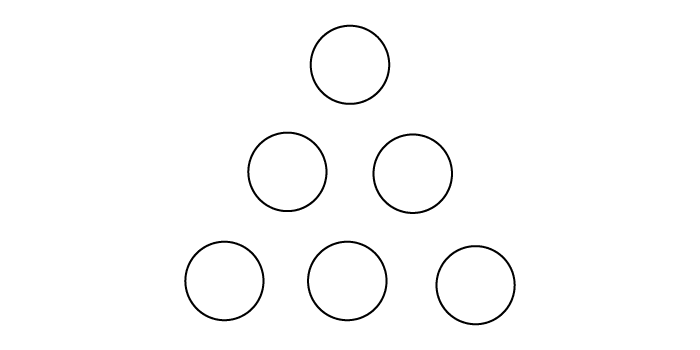
例題の答え

1人，2人，3人，6人

まずは、問題の意味を理解できているかどうか、確認してあげてください。よくわかっていないようでしたら、具体的に「2人で分けるとどうなる？」と聞いてみましょう。「3つずつもらえて、あまりが出ない」ことがわかればOKです。あとは、3人のとき、4人のとき、……と順に調べていくよう、うながしてあげてください。「あまりが出るとき」のイメージがつかめないときは、「4人だと、ひとり1個もらえて、2個あまる」ことを確認してあげましょう。

「解いてみよう」で2桁の数が出てくるようになると、九九の範囲だけで考えてしまい、2桁の答えを見落とすこともあります。その場合、「1人のとき」から順に確認してあげてください。その流れで「9人のときは？」と聞いたあと、そのまま「10人のときは？」と聞いてあげると、見落としに気づくことも多いです。

「分けていく」のが難しい場合は、おはじきなどを使って実際に分けてみるのがいいでしょう。

 

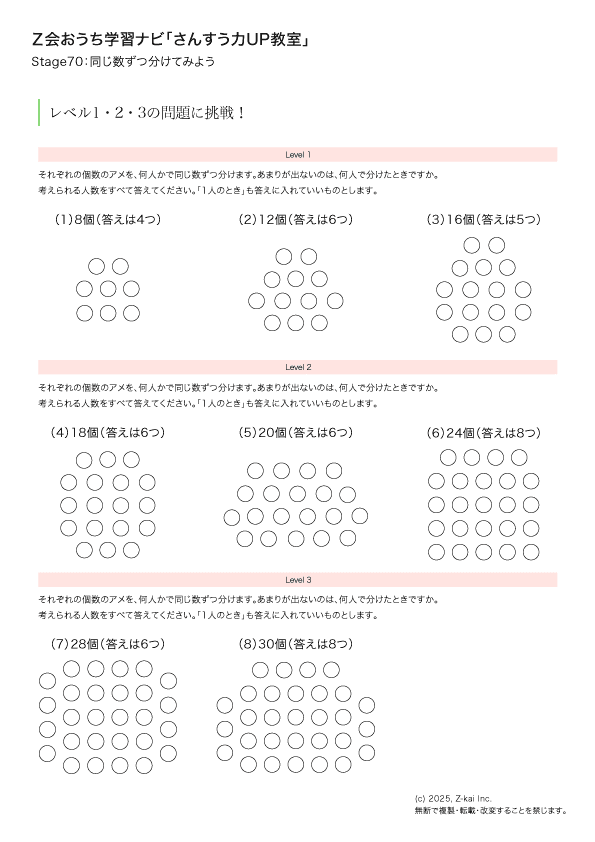
レベル１・２・３の問題に挑戦！

難度別に3段階の問題を掲載しています。ぜひ、親子で挑戦してみてくださいね。

▲画像クリックで拡大します（PDFファイル）
 

解答を確認しよう！

解答はこちら 
 

さんすう力UPのポイント

Stage64やStage67で、数や計算に対するイメージを豊かにしていくことが大事、とお伝えしましたね。今回の「分けられる数」も、その「数のイメージ」を豊かにしていくための視点の1つです。

数は、その名前の通り「数える」ための道具です。その意味ではまず、1，2，3，…と、「順に並んでいる」イメージがあるかもしれません。しかしそこから、「数えたものを分ける」ということになってくると、「数」のまた違った姿が見えてきます。「偶数と奇数」はその入り口でしょう。今まで一列に並んでいるように見えた数が、「ちょうど半分にできる数とそうでない数」という2つのグループに分けられることに気づきます。さらにいろいろな人数で分けてみると、「分けやすい数」や「分けにくい数」が存在していることにも気づくでしょう。たとえば、6個のときは「1人，2人，3人，6人」で分けられますが、1つ増やして7個にしただけで、分けられる人数が「1人、7人」のときのみになりますね。7個以外にも、2個、3個、5個などは分けられる人数が2種類しかありませんが、こういった数はまた「素数」というグループに分類されます。この「素数」には、2が仲間に入ったり、逆に9が入らなかったりと、「偶数・奇数」とは少し違うふるまいを見せます。なんだか難しいと感じるか、不思議で面白いと感じるかは、その人の価値観によると思いますが、いずれにしても、全部同じように見える「数」にもいろいろな個性があり、その性質によっていろいろなグループ分けができる、ということを感じ取ることはできるでしょう。その「数の個性」に少し触れてほしいというのが、今回の問題の狙いです。

冒頭でお伝えしたように、「同じ数ずつに分ける」というのは、掛け算・割り算にもつながっていく話ですね。しかしだからと言って、今回の問題で「割り算だよね」と先にお子さまに伝える必要はありません。むしろ、自分で気づいていないようなら、先回りしてそれを伝えることは、お子さまの「割り算」への理解を深める機会を奪ってしまうことにもなるでしょう。同じように、掛け算や割り算をまだ学習していないお子さまに対して、この問題を解くためにそれらを教える必要もありません。割り算の学習がまだであっても、実際にアメを分けることは（もしくはアメの代わりにおはじきなどを分けることは）可能です。むしろ、割り算の学習を本格的に始める前に、「分ける」経験を積んでおくことで、割り算の学習へのハードルを下げることができるでしょう。お子さまが「数」と触れ合い、仲良くなっていく様子を、ぜひ温かく見守ってあげてください。

 

---

いかがでしょうか。

気づけば今年も終わりですね。今年は人間ドックに行くと言っていた気もするのですが、結局行っていないような気もします。この一年を通していろいろ思うところはあり、生活リズムの見直しも少しずつ進めていっております。ずっと昔に買った立派な圧力鍋でまた定期的に豚の角煮を作れる程度に、生活に余裕を持てるようになれるといいな、と思っています。

それではまた来年！

 

「小田先生のさんすう力UP教室」の記事一覧はこちら