(1)
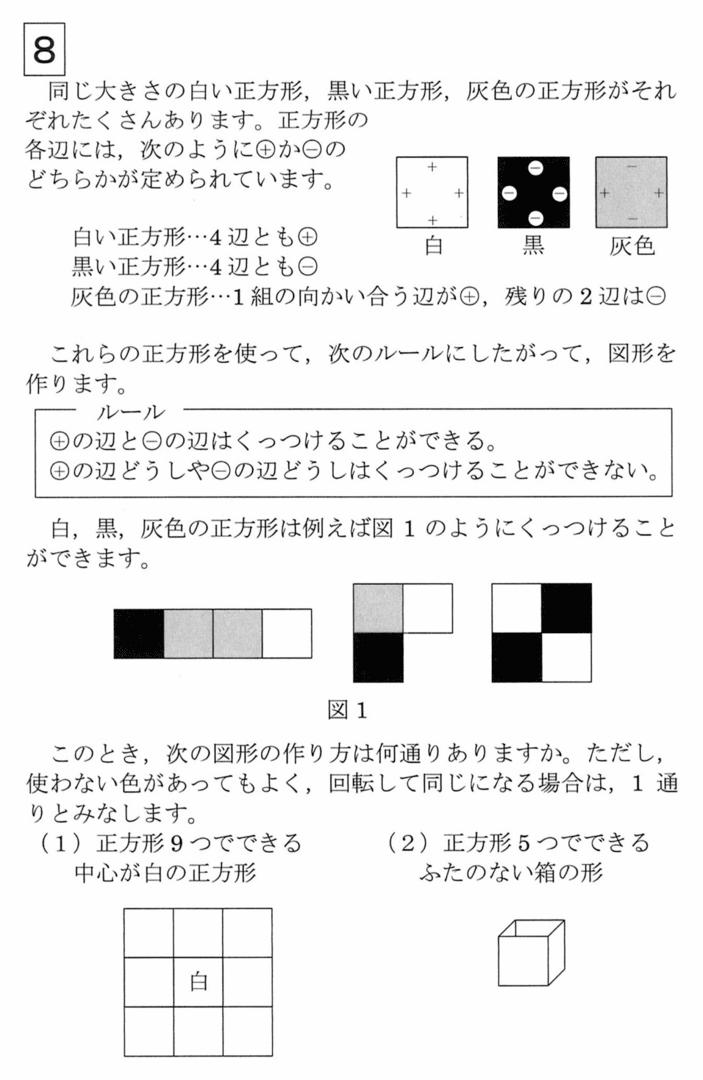
問題文のルールより、中心にある白の正方形のとなりの正方形は、黒い正方形か灰色の正方形になります。ここで、中心の白い正方形の上下左右の正方形を①~④、それ以外の正方形を5~8とします。

回転して同じになる場合は1通りとみなすことに注意して、考えられるパターンをすべて書き出します。
・①~④がすべて黒い正方形のとき
5~8は、すべて白い正方形になるので、1通りに決まります。

・①~④がすべて灰色の正方形のとき
5~8は、すべて黒い正方形になるので、1通りに決まります。
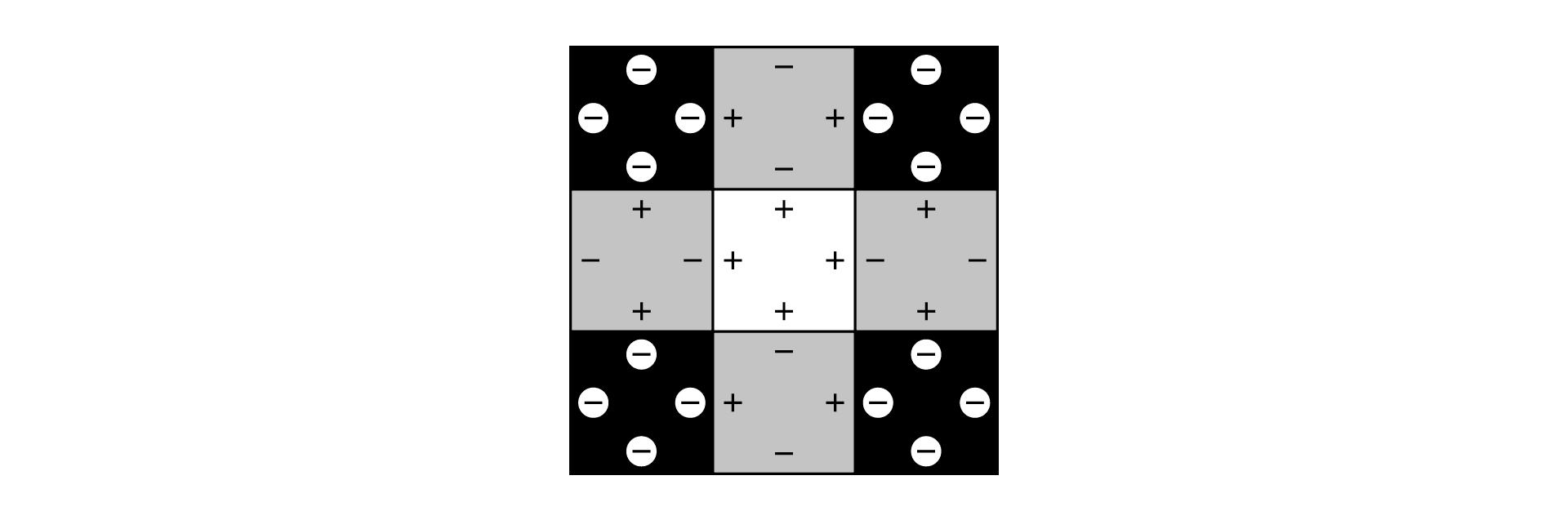
・①~④のうち、3つが黒い正方形のとき
3つの黒い正方形の選び方は1通り。
5~8も1通りに決まります。
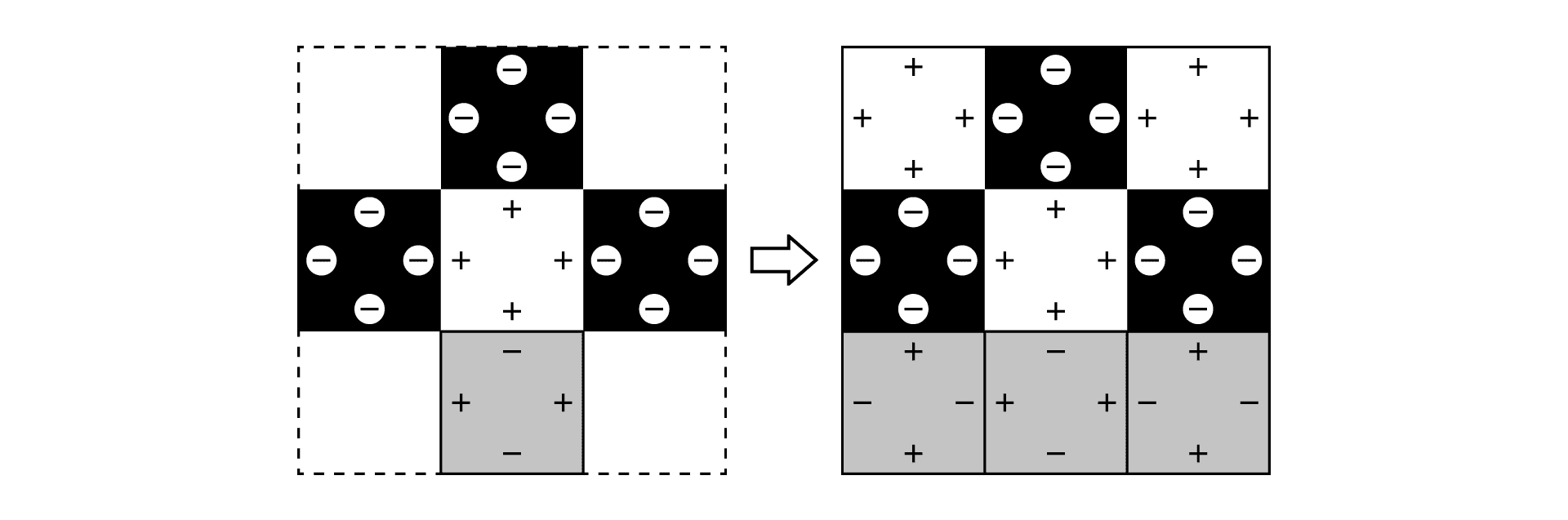
・①~④のうち、1つが黒い正方形のとき
1つの黒い正方形の選び方は1通り。
5~8も1通りに決まります。
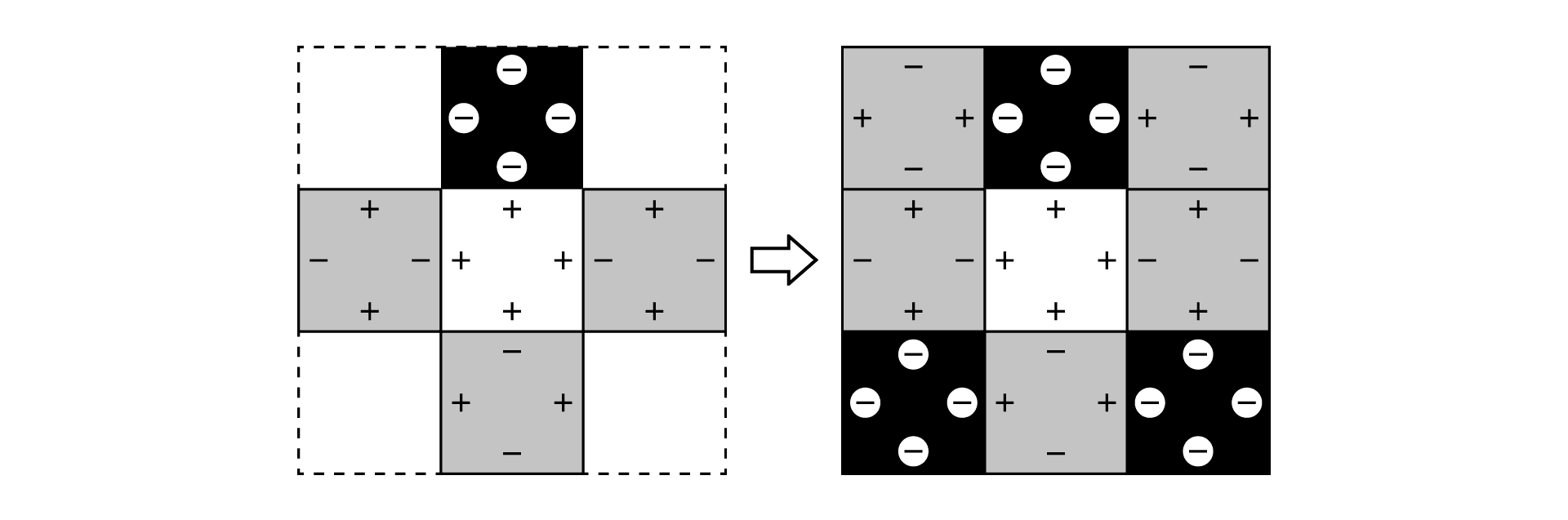
・①~④のうち、2つが黒い正方形のとき
2つの黒い正方形の選び方は次の(ア)と(イ)の2通り。
(ア)中心の白の正方形の向かい合う2辺に黒い正方形をくっつける場合
5~8は、1通りに決まります。
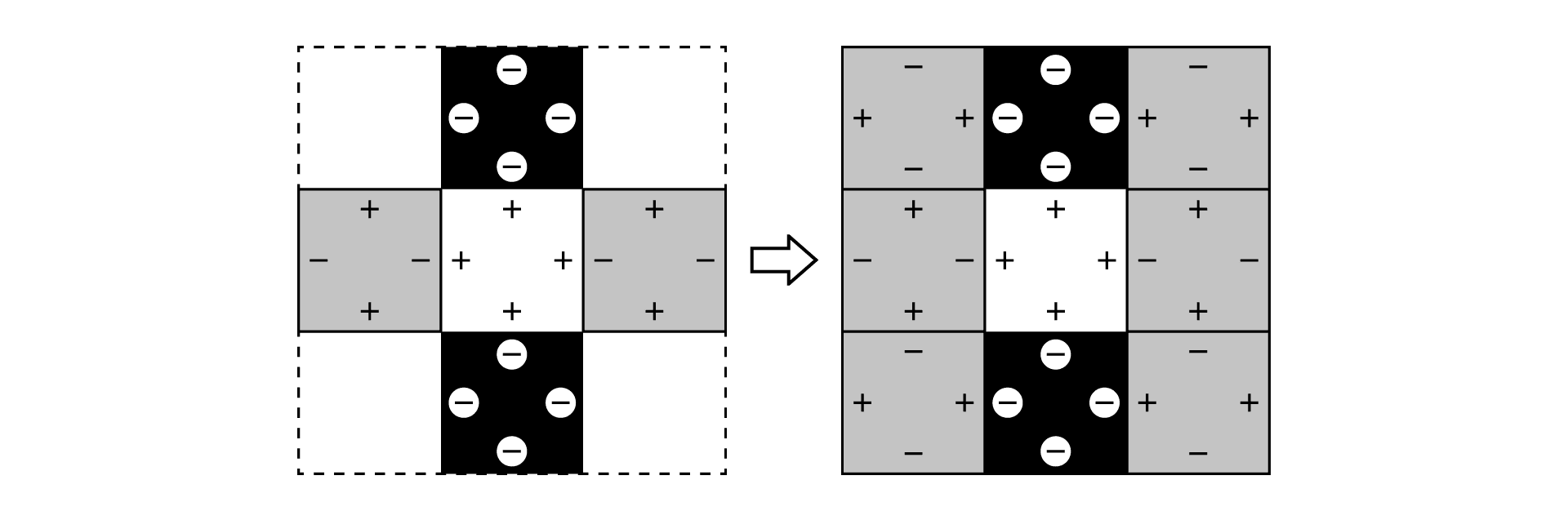
(イ)中心の白の正方形のとなり合う2辺に、黒い正方形をくっつける場合
5~8は、1通りに決まります。
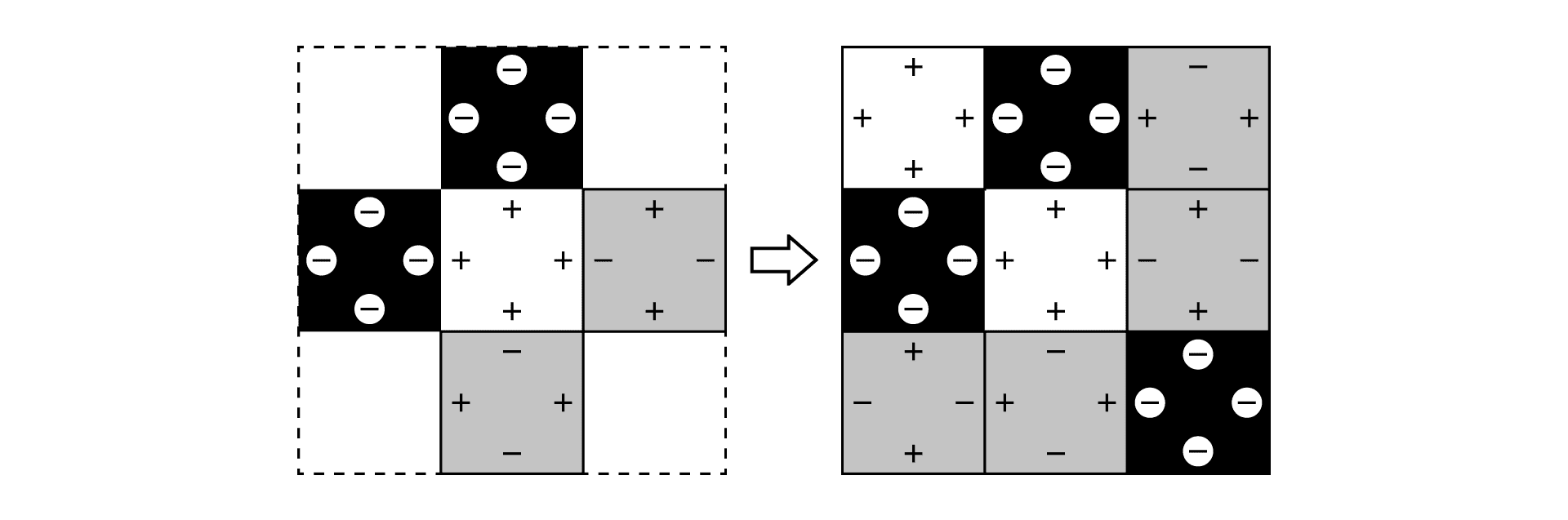
よって、正方形9つでできる中心が白の正方形の作り方は、6通りとわかります。
(2)
(1)の9つの正方形から5~8を除いたものが、正方形5つでできるふたのない箱の展開図になります。このとき、箱の底面は白い正方形になっているので、箱の底面が、白い正方形のとき、黒い正方形のとき、灰色の正方形のときでそれぞれ考えます。
・箱の底面が、白い正方形のとき
(1)で書き出した6通りのうち、箱を組み立てるときに辺どうしをくっつけることができるのは、次の1通りだけです。
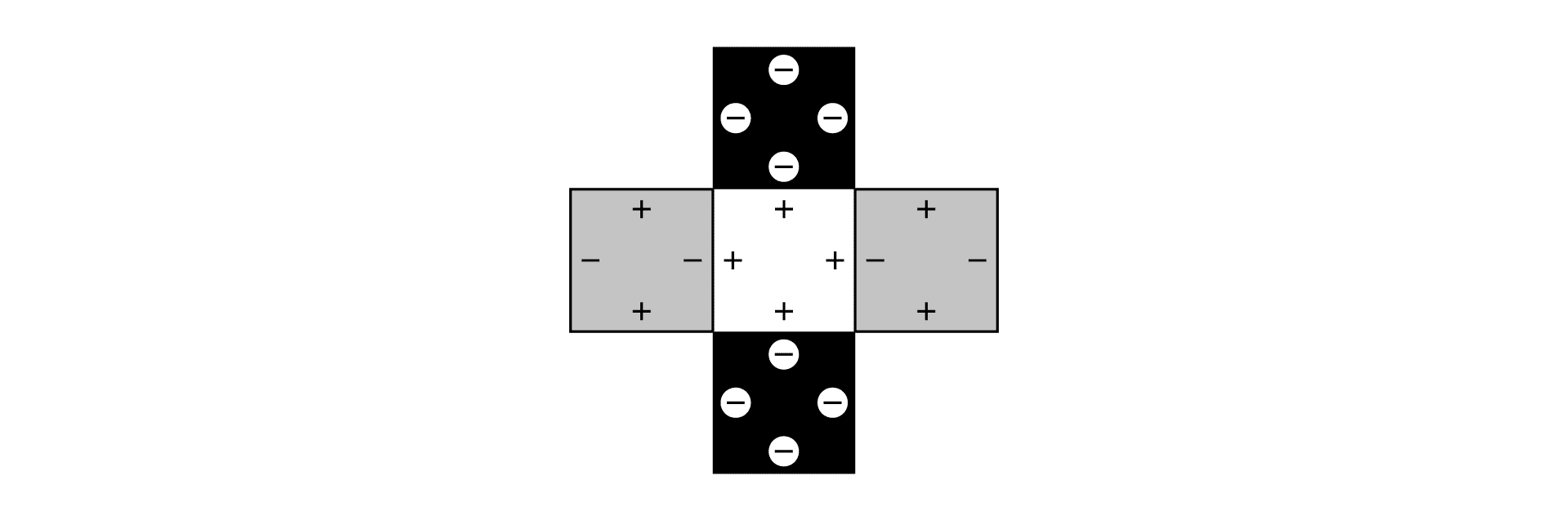
・箱の底面が、黒い正方形のとき
箱の底面が、白い正方形のときと同様に考えて、次の1通りがあります。
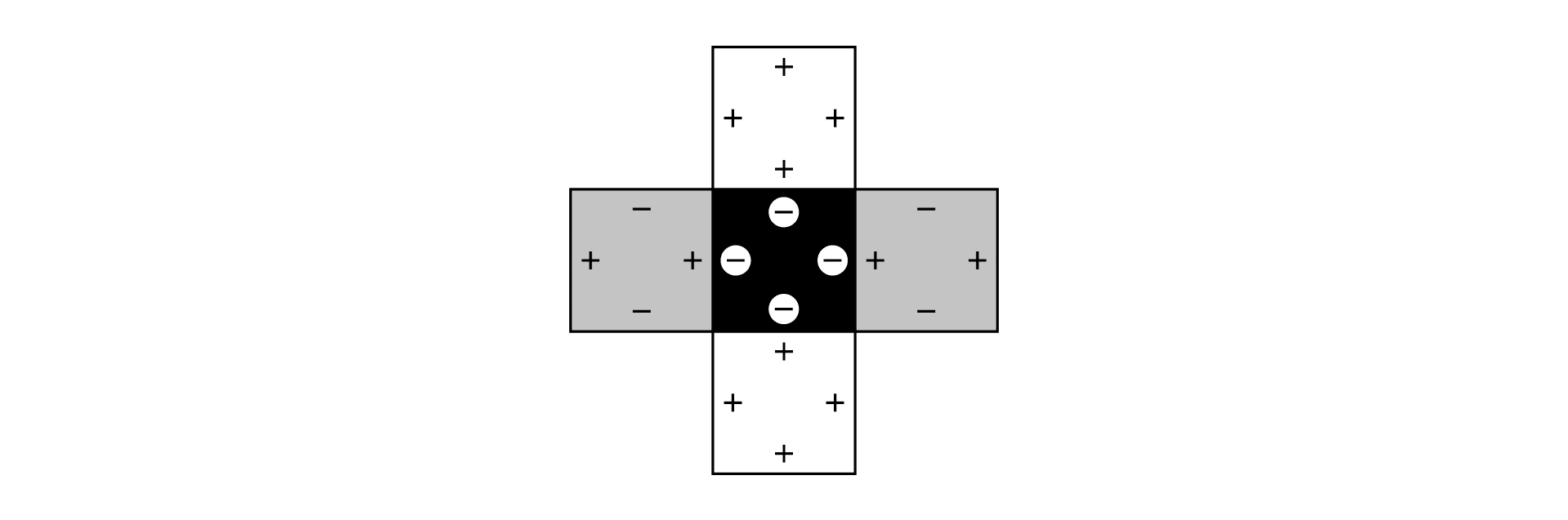
・箱の底面が、灰色の正方形のとき
(ウ)①が黒い正方形のとき
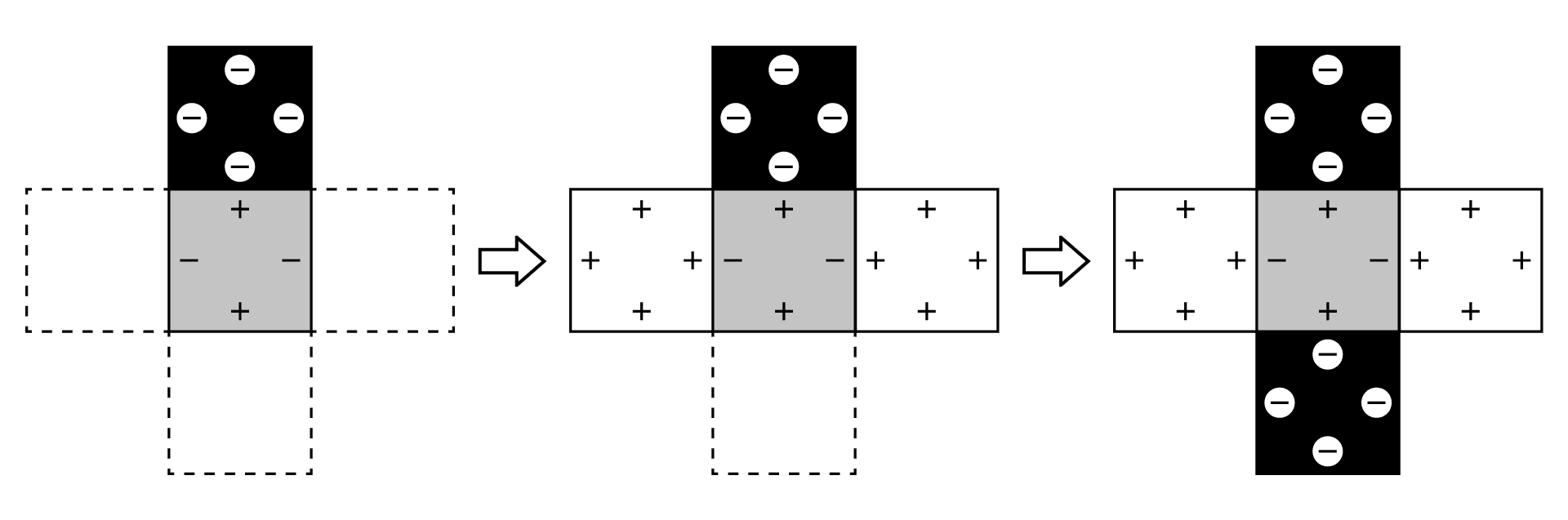
(エ)①が白い正方形のとき
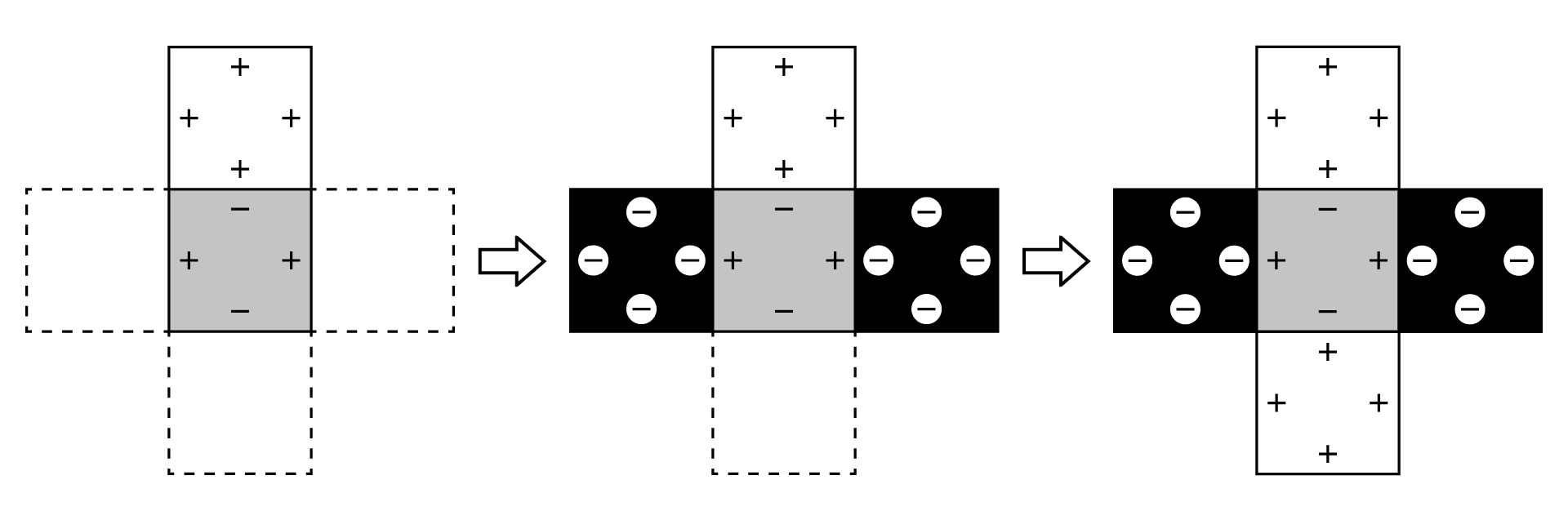
これは回転すると(ウ)と同じになるので、(ウ)と(エ)で1通りとわかります。
(オ)①が灰色の正方形のとき
次のような1通りとわかります。
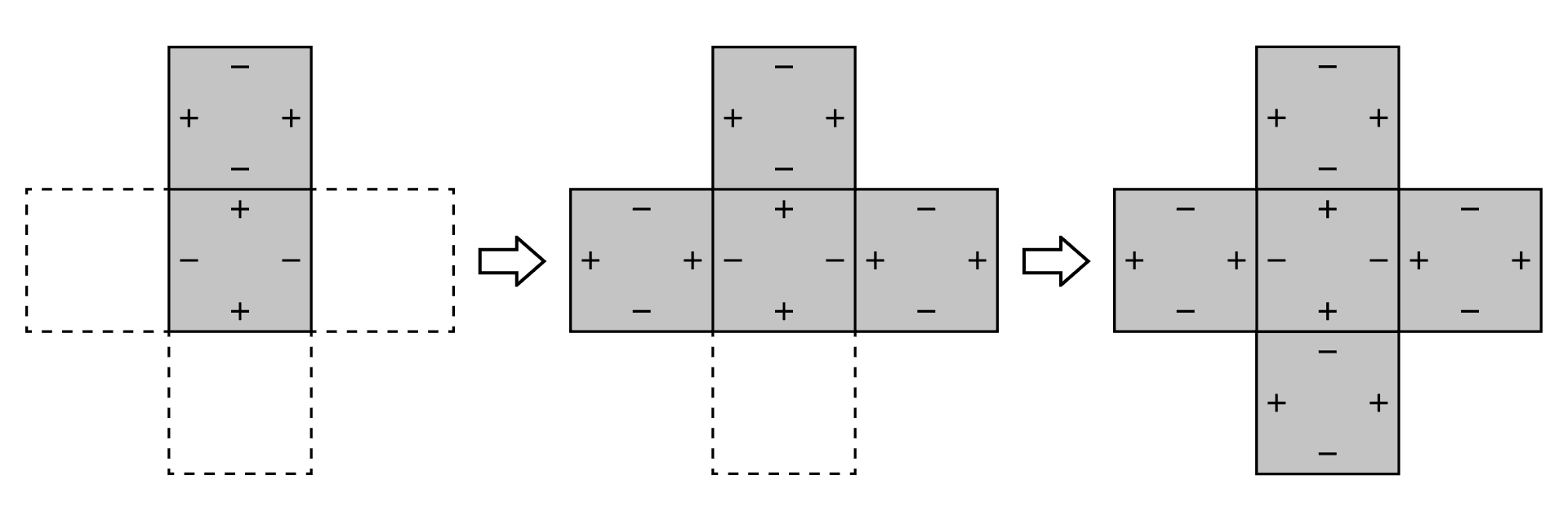
よって、正方形5つでできるふたのない箱の形の作り方は、4通りとわかります。