こんにちは、最近またガムテープを買ってしまった小田です。ガムテープって、必要なタイミングで見当たりませんよね。そして、仕方がないので新しく買うと、買ったあとに見つかったりしますよね。今回も、無事買ってきたものを開封して少し使ったタイミングで、以前買ったものが発掘されました。そうやって「ちょっとだけ使ったガムテープ」がたまっていくんですよね。どうすればいいのでしょうか。

さて今回は、すべてのパターンを書き出していく問題です。考えられるものをどんどん書いていけばいいのですが、“すべてを書き切る”というのは結構難しかったりします。本当にほかにはないかな、と考えながら、その難しさを楽しんでみてください。
それでは早速行ってみましょう。

 

Stage51：ほかにもないか探してみよう

例題

図のような四角形を、赤、青、黄色の3色でぬりわけます。
隣りあう場所に、同じ色をぬってはいけません。使わない色があってもいけません。回転させたり裏返したりして同じになるぬり方は同じものとするとき、考えられるぬり方をすべて答えてください（全部で3通りあります）。

例題の答え（例）

まずは問題の意味を理解しているかどうかの確認ですね。3カ所に区切られた枠に、それぞれ1色ずつぬっていく、という問題です。1つの枠につき1色です。例題では「3カ所に3色」なので、結果的に同じ色を2回使うことはできませんが、あとの問題では同じ色を何回か使う場面も出てくるので、そこは誤解のないよう伝えてあげてください（同じ色を何回か使う問題では、「同じ色が隣り合ってはいけない」ことを改めて確認してあげてください）。

「ぬり方のルール」を理解した様子であれば、あとは温かく見守ってあげましょう。回転させたり裏返したりして同じものは同じぬり方とみなすので、そういった“同じもの”があれば、「これとこれは同じぬり方だね」と伝えてあげてください。同じかどうかの判断が難しそうであれば、実際に回転させたり裏返したりして確認してあげればいいでしょう。それでもピンときていない場合は、ぬった色を順に「青、赤、黄色の順になっているね」と言葉で確認してあげてください。

ちなみに、保護者の方が「同じぬり方かどうかわかりづらい」場合には、真ん中の色に注目しましょう。真ん中の色が決まれば、残りの2色はどちらにぬっても回転させると（もしくは裏返すと）同じぬり方になります。つまり、真ん中の色が同じものがあれば、それは同じぬり方と判断してかまいません（これはあくまで保護者の方のためのヒントですので、お子さんにはとくに伝えなくて大丈夫です）。
3つのぬり方をすべて見つけることができれば、正解です（もちろん、上記と回転させたり裏返したりして同じになるものであればOKです）。残りひとつがなかなか見つからない、ということもあるかもしれませんが、そのときは適度にはげましてあげてください。

 

解いてみよう

図のような四角形を、決められた色でぬりわけます。
隣りあう場所に、同じ色をぬってはいけません。使わない色があってもいけません。同じ色を何回か使うのは構いません。回転させたり裏返したりして同じになるぬり方は同じものとするとき、考えられるぬり方をすべて答えてください。

(1)　ぬる色：赤、青、黄色（全部で3通りあります）
(2)　ぬる色：赤、青、黄色、緑（全部で6通りあります）

 

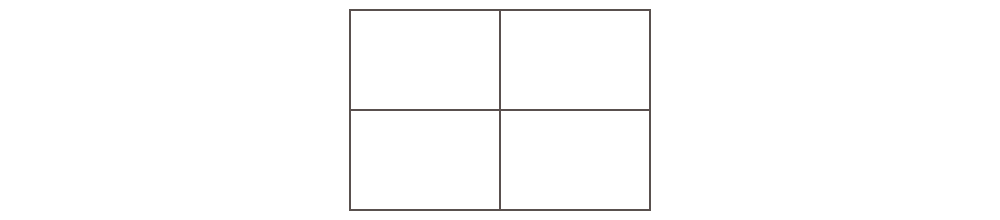
図のような四角形を、決められた色でぬりわけます。
隣りあう場所に、同じ色をぬってはいけません。使わない色があってもいけません。同じ色を何回か使うのは構いません。回転させたり裏返したりして同じになるぬり方は同じものとするとき、考えられるぬり方をすべて答えてください。

(3)　ぬる色：赤、青、黄色（全部で3通りあります）
(4)　ぬる色：赤、青、黄色、緑（全部で6通りあります）

 

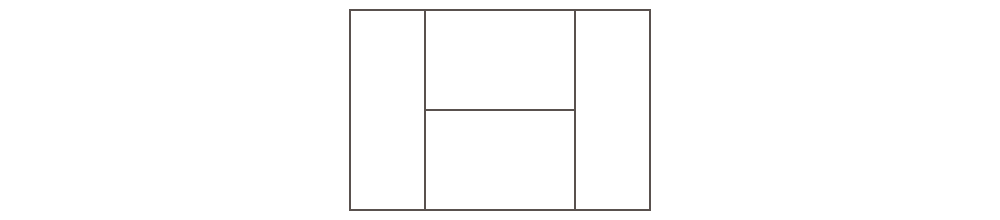
図のような四角形を、決められた色でぬりわけます。
隣りあう場所に、同じ色をぬってはいけません。使わない色があってもいけません。同じ色を何回か使うのは構いません。回転させたり裏返したりして同じになるぬり方は同じものとするとき、考えられるぬり方をすべて答えてください。

(5)　ぬる色：赤、青、黄色（全部で9通りあります）
(6)　ぬる色：赤、青、黄色、緑（全部で12通りあります）

 

解答（例）

 

 

 

さんすう力UPのポイント

今回の問題、パターンが増えてくると、最後まで探しきるのは結構難しいですよね。残り1つがなかなか見つからなかったりして、本当にほかにもあるのかな、と感じる場面もあるでしょう。そうやって、「ほかにないかな」と探していく経験を積んでほしい、というのが今回の問題の狙いです。
算数を学習するうえで、「論理的な思考」の重要性が語られることは多いですね。その「論理的な思考」ができるようになるための、要となる力のひとつが「ほかにもないか探していく力」です。「論理的な考え方」というと、「AだからB、BだからC」という感じで“順番につないでいくこと”が大事だという印象が強いかもしれません。しかし本当に重要なことは、“つないでいくこと”そのものではなく、その“つながり”が本当に正しいかどうかです。そして、算数で「本当に正しい」というのは、「Aという条件では“必ず”Bとなる」ということです。「Aである」という条件が与えられたとき、結論の可能性としてB以外にCがあるにもかかわらず、「AだからBだ」としてしまうと、それは算数では「論理的には誤り」となるのです。実際、算数の問題を解いていて、「こういう条件だからこうなるはず」と“決めつけて”しまって間違ってしまった、という経験をもつ人も多いでしょう。それを防ぐために、「本当に必ずそうなるのか」「ほかにも結論の候補がないのか」と考える姿勢、そして、探していく力が必要なのです。

候補をすべてあげていくことの重要さ、そしてその難しさがわかってきたら、あとは実際に列挙していく技術を身につける必要があるでしょう。たとえば、今回の問題であれば、「どこに注目するか」が大事になってきます。例題では、「真ん中にぬる色」に注目すると、うまく調べ上げていくことができますね。「解いてみよう」の問題も順に解説していくと、(1)では「2回ぬる色」に注目するといいでしょう。「裏返して同じものは同じ」なので、「左上と右下が同じ色」のものと「右上と左下が同じ色」のものは同じパターンとなります。2回ぬる色を決めると、残りの2箇所はどうぬっても回転させれば同じパターンになりますね。(2)は「赤をぬる場所」に注目するといいでしょう。赤をどこにぬっても、回転させたり裏返したりすれば、「赤を左上にぬったもの」と同じパターンにすることができます。(3)は同じ色をぬれる場所が「左端と右端」しかないので、ここを何色にするかを決めればいいですね。(4)も同じく、「左端と右端」の組み合わせを考えていく、というのがひとつの手段となります。(5)も「2回ぬる色」の場所に注目するといいでしょう。「1番目と3番目が同じ色」と「2番目と4番目が同じ色」は、回転させると（もしくは裏返すと）同じパターンとなります。それ以外には「両端が同じ色」もありますね。これらを順に調べていきます。(6)は「赤をぬる場所」に注目すると、「左端か左から2番目」となりますね（左から3番目は左から2番目と、右端は左端と同じになります）。

もちろん、この「注目する場所」に“正解”はありません。上であげたポイントも、それぞれひとつの例でしかありません。正解がないということは、パターン化することが難しい、ということでもあります。いろいろなアイディアをストックしておき、問題に応じて必要なものを使っていく、という力が求められるのです。とても難しいですね。

今回の問題で、スムーズに正解できるようになることは、それほど期待していません（上記のポイントも、例題の解説でふれたように、お子さんがそこにたどり着けることを目的とはしていません）。それよりもむしろ、「なかなかうまくいかない」経験を積んでもらうことで、「“候補をすべて挙げる”ことは難しいことである」ということを実感することが大事です。技術が必要になる、とお伝えしましたが、その技術を身につけよう、と思えるようになるためには、やはりその“難しさ”を痛感する必要があるからです。お子さんがうまくすべて見つけきれなくても、まずはぜひ温かく見守ってあげてほしいと思います。
 

---

いかがでしょうか。

先日沖縄に旅行して以来、“もずく”にはまっています。沖縄で食べてみておいしかったから、ということではあるのですが、お土産では買わず、近所のスーパーで買っています。普通にスーパーで買い物をしているときに見かけて、そういえばおいしかったな、と思い出した、ということではあるのですが。まあ、パックの方が便利というのもありますしね。健康にも良さそうなので、しばらく継続して食べてみたいと思います。

それではまた来月！

 

「小田先生のさんすう力UP教室」の記事一覧はこちら