さんすう力を高めるにはどうしたらいいの? まあ、そんなに難しく考えないで、まずはお子さまと一緒に問題に取り組んでみましょうよ。
(執筆:小田敏弘先生/数理学習研究所所長)
※本記事は、2024年1月25日に「Z-SQUARE」上で掲載した記事を一部修正の上、再掲しています。

さんすう力を高めるにはどうしたらいいの? まあ、そんなに難しく考えないで、まずはお子さまと一緒に問題に取り組んでみましょうよ。
(執筆:小田敏弘先生/数理学習研究所所長)
※本記事は、2024年1月25日に「Z-SQUARE」上で掲載した記事を一部修正の上、再掲しています。
![]() こんにちは、年末年始に体重が2キロ増えた小田です。毎年「今年こそは人間ドックに行くぞ!」と思い続けて何年か経ちました。そういえば、5月号あたりでもそんなことを言っていましたね。結局年内には行けずじまいでした。旅行とセットになっているプランもよさそう、とかも言っていましたが、それはそれで日程の調整が面倒な気もしてきました。まあでも確か「○○歳の目標」だったはずなので、誕生日を迎えるまでに行けたらいいな、と思います。今年も、ほどほどに健康に気をつけながら生きていきたいと思います。
こんにちは、年末年始に体重が2キロ増えた小田です。毎年「今年こそは人間ドックに行くぞ!」と思い続けて何年か経ちました。そういえば、5月号あたりでもそんなことを言っていましたね。結局年内には行けずじまいでした。旅行とセットになっているプランもよさそう、とかも言っていましたが、それはそれで日程の調整が面倒な気もしてきました。まあでも確か「○○歳の目標」だったはずなので、誕生日を迎えるまでに行けたらいいな、と思います。今年も、ほどほどに健康に気をつけながら生きていきたいと思います。
さて、今回は図形の問題です。同じ形に分ける、というシンプルなルールですが、だからといって解くのが簡単というわけではありません。むしろ、慣れていないと結構苦戦したりもするでしょう。解けなければいけない問題ではないので、その難しさもぜひ楽しんでほしいと思います。
それでは早速行ってみましょう。
下の図形を、4つの同じ形に分けてください。ただし、回したり裏返したりして同じ形になるものであれば、同じ形として構いません。
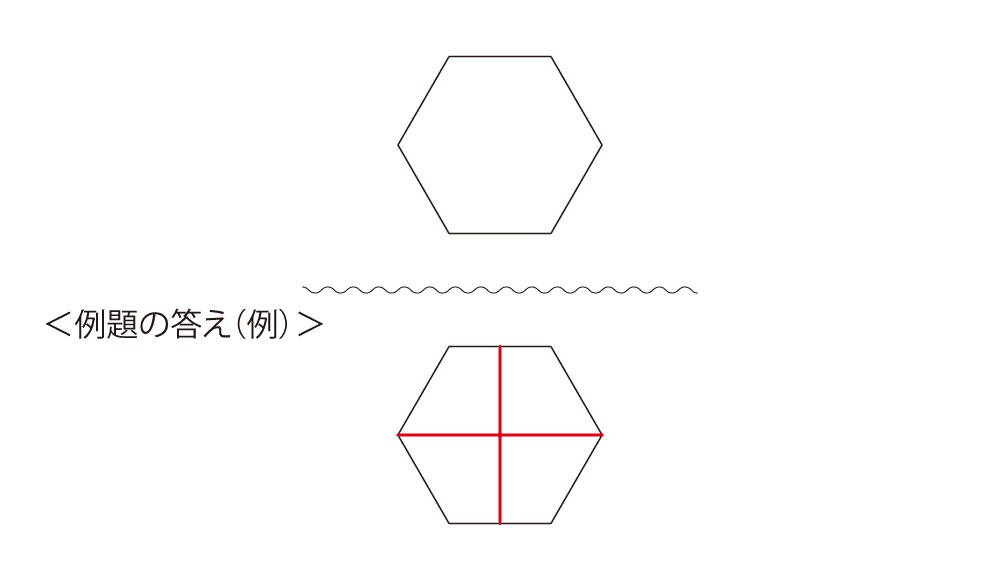
まずはいつも通り、問題の意味がわかっているか確認してあげてください。「同じ形」というのはここでは「合同」のつもりで書いていますので、「大きさが違ってはいけない」ことは伝えてあげましょう。また、問題文に書いてある通り、回転させたり裏返したりして同じならOKです。
慣れないうちは苦戦すると思いますが、最初は温かく見守ってあげましょう。冒頭でもお伝えしたように、「解けなければいけない問題」ではありません。解けないなら解けないで、その「解けなさ」を楽しんでもらえれば十分です。お子さんが苦戦している場合は、「難しいね」と共感してあげてください。
お子さんが答えを出したら、分けた形が同じになっているかどうかを確認してあげましょう。4つの同じ形に分けられていたら正解です。分ける個数が違っていた場合は、「4つに分けるんだよ」と伝えてあげてください。同じ形になっていなければ、「ここが少し違う形だね」と指摘してあげましょう。だいたいで書けていればいいので、あまりうまく書けていなくても、雰囲気があっていたら正解にしてあげてください。
それぞれの図形を、決められた数の同じ形に分けてください。ただし、回したり裏返したりして同じ形になるものであれば、同じ形として構いません。
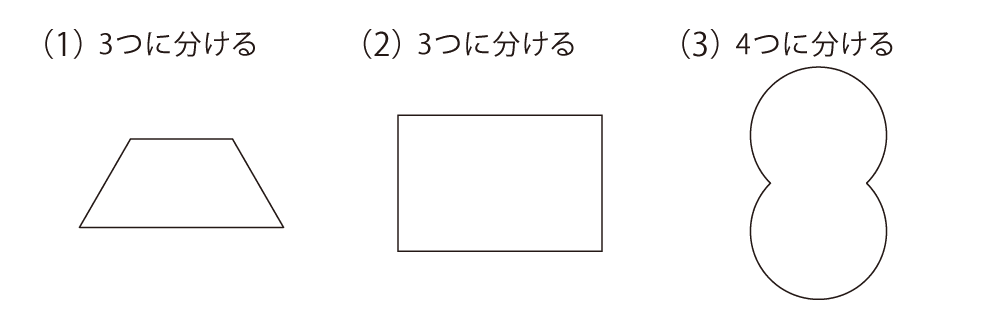
それぞれの図形を、決められた数の同じ形に分けてください。ただし、回したり裏返したりして同じ形になるものであれば、同じ形として構いません。
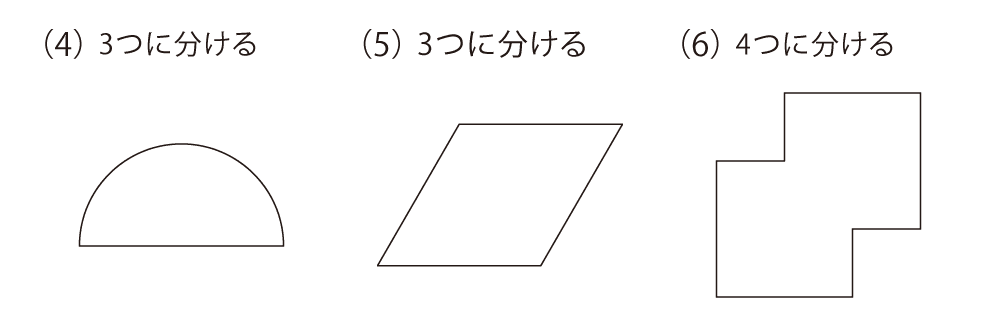
それぞれの図形を、決められた数の同じ形に分けてください。ただし、回したり裏返したりして同じ形になるものであれば、同じ形として構いません。
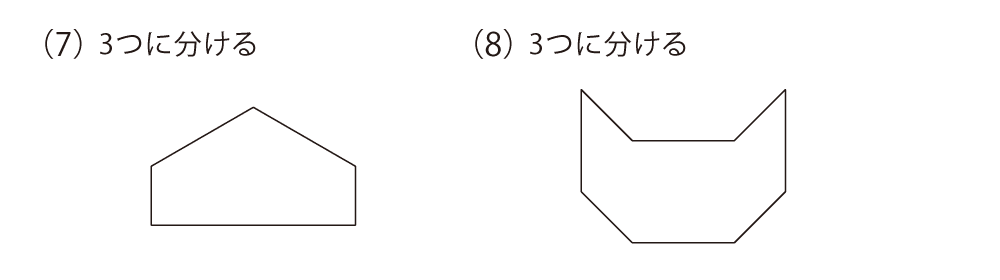
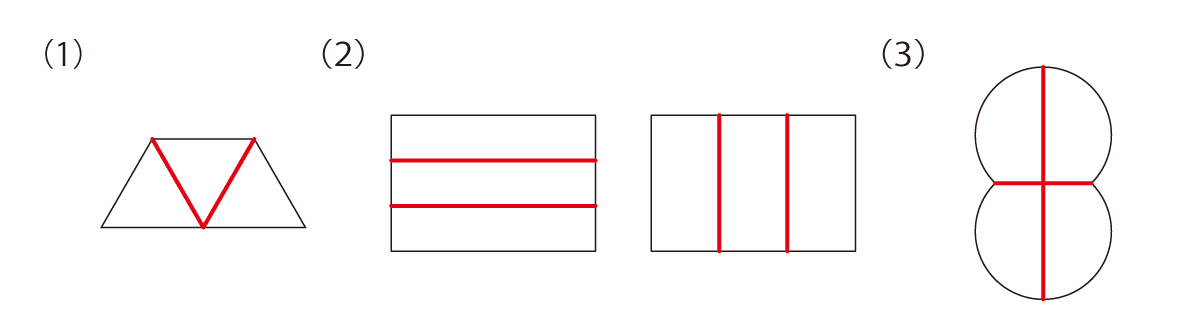
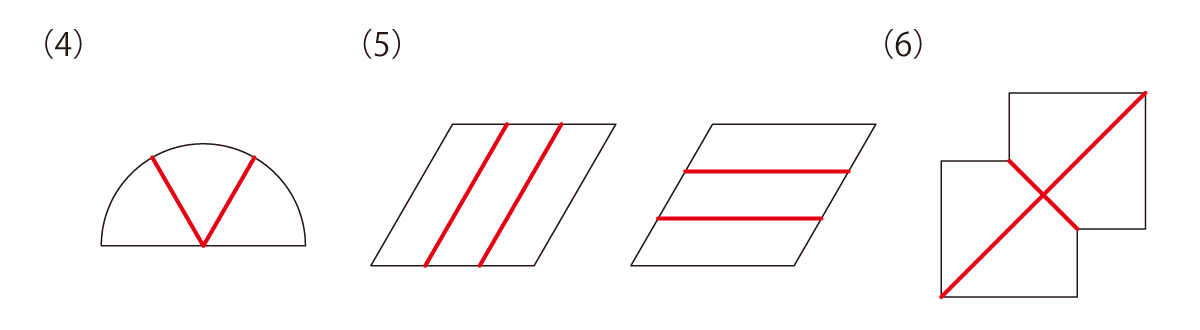
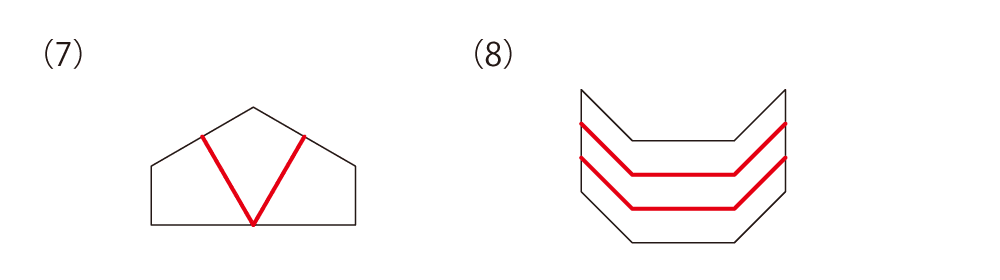
今回のような問題は、「解ける人はスムーズに解けるけど、解けない人はまったく解けない」というイメージがありますね。こういう問題を見てしまうと、算数の問題・図形の問題を解くためには、何かしら“ひらめき”のようなものが必要だと思ってしまうのかもしれません。確かに、算数の問題を解く中で“ひらめき”が必要な場面もありますが、“ひらめき”は「天から授かった特殊能力」ではありません。“ひらめき”の源泉となるのは、単純に「経験」なのです。
たとえば、「正方形を4つの同じ形に分ける」方法を考えてみてください。いろいろな正解が考えられますが、図のように「十字に切って4つに分ける」方法も、正解のひとつですね。
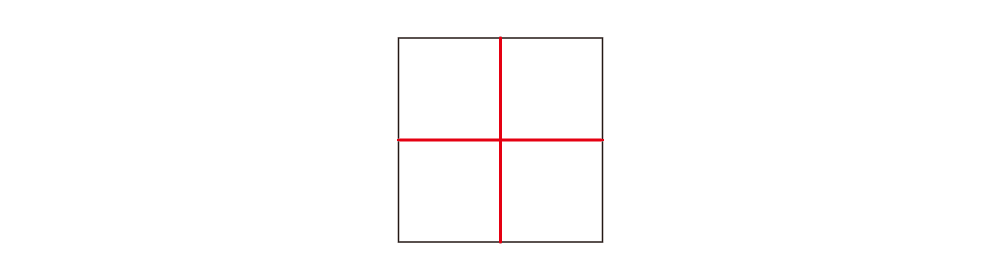
この図と、例題の解答を見比べてみてください。言われてみれば、よく似ていると思いませんか。「正六角形を4つに分ける」問題自体が初見だったとしても、「正方形を4つに分ける」問題で、この分け方をやったことがあれば、正六角形の問題でも「十字に切る」方法を“ひらめく”確率があがります。ついでに言えば、「解いてみよう」の(3)や(6)も同じですね。(6)は斜めになっているので少し気づきにくいかもしれませんが、いずれも「十字に切って4つに分ける」問題でした。もちろん、「経験」があったからと言って、必ず目の前の問題につなげられるわけではありませんが、「経験」がない状態から“ひらめく”ことは相当難しいことであるとは言えるでしょう。
“ひらめき”を得られるようになりたければ、まずは「経験」を増やしていくことが大事です。ここで言う「経験」は、単に「類題を解いた“経験”」だけではありません。たとえば、「十字に分ける」という構図は、別に算数の問題だけに出てくるものではありません。「四つ折り」という言葉もあるように、紙を折るときにこういった折り方をすることはよくありますね。「正方形を四つ折りする」というのは、まさに折り紙などでもよくある場面です。そういった「紙を4つに折る」経験があれば、たとえ算数の問題としてこの問題を解いたことがなくても、“ひらめき”を得られる可能性は十分出てくるでしょう。
保護者の方からのよくあるご相談のひとつに、「算数ができるようになるために、何をさせればいいですか」というものがあります。答える側としては、回答に慎重になる質問のひとつです。子ども本人から、「算数ができるようになるために、何を“すれば”いいですか」と聞かれたら、答えは簡単で、それは「算数の勉強」と答えるでしょう。算数ができるようになる、というのは、「算数のなかで扱われるもの」についての理解を深めていく、ということです。その理解を深めるために体系的にまとめたものが“算数”という教科である以上、“算数”を勉強するのが「算数ができるようになる」ための王道なのです。ただ、これはもちろん、学習者本人が「算数の勉強をやりたい・算数ができるようになりたい」と言っている場合に限ります。外から強制された「勉強」は、やはり効率がよくありません。その意味で、「何を“させれば”いいでしょうか」という、外から働きかけることが前提である質問に対しては、「算数の勉強」とは答えにくいのです。
低学年のお子さんの場合はとくに、「算数の勉強」を体系的に進めていくのが難しい場合も多いでしょう。その時期のお子さんには、ぜひ「経験」を増やしていってほしいと思っています。ただ、その際に気をつけてほしいことがひとつあります。それは、「算数ができるようになるため」と思わないことです。そもそも「算数の勉強のために〇〇をやらせる」というのは、その〇〇に対して失礼だと個人的には思っています。その〇〇には〇〇のおもしろさがあります。「算数の勉強のため」としてしまうと、得られるものも限られてしまい、とてももったいないですね。たとえば折り紙で遊ぶのであれば、やはり折り紙そのものを楽しむことが、一番豊かな経験を得られるはずです。
お伝えしたいのは、一見“勉強”と関係ないように見えても、その経験は“勉強”に活きてくる、ということです。まずは、あまり“勉強”にこだわらずに、いろいろな種類の経験を積めるよう、サポートしてあげてほしいと思います。
![]() いかがでしょうか。
いかがでしょうか。
また新しい一年が始まりましたね。そういえば生活習慣の話で言えば、昨年は「血圧・体重・活動量(歩数など)を記録する」という習慣が新たに身につきました。もちろん、測り忘れる日もちょくちょくありますが、「しばらくやってないなぁ」ということはないので、一応“身についた”と言ってもよいでしょう。測って記録するだけで何がどうだという話ですが、個人的にはまず一歩前進したつもりではあります。記録を管理できるアプリがあったりして、日々の負担が少ないのがよかったのかもしれません。今年は、「無理に大きく変える」のではなく、試行錯誤しながら「負担の少ない少しいいこと」を探していこうと思います。
それではまた来月!

文:小田 敏弘(おだ・としひろ)
数理学習研究所所長。灘中学・高等学校、東京大学教育学部総合教育科学科卒。子どものころから算数・数学が得意で、算数オリンピックなどで活躍。現在は、「多様な算数・数学の学習ニーズの奥に共通している“本質的な数理学習”」を追究し、それを提供すべく、幅広い活動を展開している(小学生から大人までを対象にした算数・数学指導、執筆活動、教材開発、問題作成など)。
公式サイト:http://kurotake.net/
主な著書