こんにちは、今年も無事誕生日を迎えた小田です。歳をとるのは実に1年ぶりなので、うまく歳を取れるかどうか不安もあったのですが、今年もつつがなく年齢を増やすことができました。そこそこいろいろあった一年ではありましたが、大過なく過ごせたことに感謝しつつ、また次の誕生日までのんびりと、しかし着実に生きていきたいと思います。

　さて、今回は図形のパズルです。2種類のパネルを使って、いろいろな形を作ってみましょう。慣れないうちは難しいかもしれませんが、その場合は実際に形を切り取って並べてみてください。

　それでは早速行ってみましょう。

Stage38：図形のセンスを身につけよう

例題

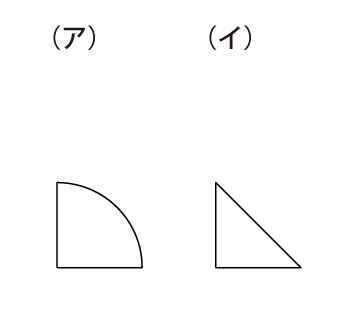
図の（ア）と（イ）のパネルをそれぞれ何枚か並べて、（ウ）の形を作ってください。

例題の答え

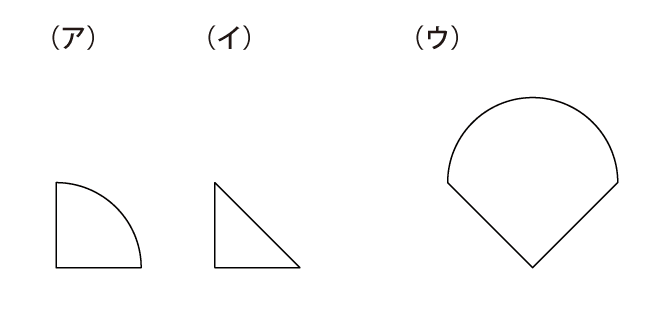
今回は、問題の意味は大丈夫そうですね。特に引っかかるところもないでしょう。まずはお子さんの様子を温かく見守ってあげてください。慣れないうちは、形がうまく描けなかったりもしますが、そういった様子も含めて、「子どもにはこういうふうに見えているんだ」と受け止めてあげてください。

大きさが小さかったり大きかったりするようなら、「もう少し大きい（小さい）よ」と伝えてあげて構いません。自分で長さを測ることができるお子さんであれば、長さを測って確認するよう伝えてもいいでしょう。形を無理に詰め込んでいたりするようでしたら、まずは形をよく見るよう促します。それでもいまいちピンとこないようなら、冒頭にも書いたとおり、実際に形を切り取って並べるのがいいでしょう。手が動かない場合も、やはり実際に並べられるようにしてあげてください。

　お子さんが答えを出したら、あまりうまく描けていなくても、だいたいの位置関係があっていれば正解にしてあげましょう。枚数が違う（無理に詰め込んでいる）ようなら、「実際に並べてみようか」と伝えて、実際に並べてみるよう促してあげてください。

解いてみよう

図の（ア）と（イ）のパネルをそれぞれ何枚か並べて，（1）〜（8）の形を作ってください。

解答（例）

さんすう力UPのポイント

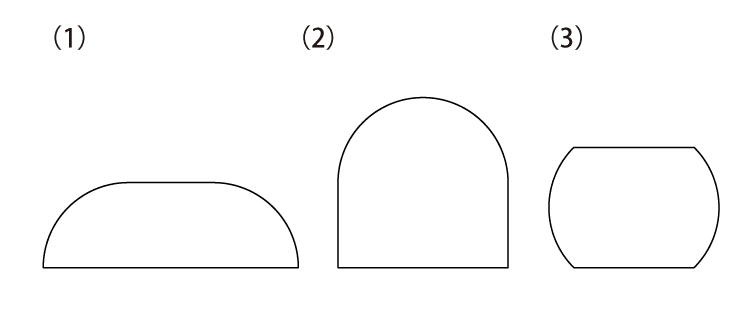
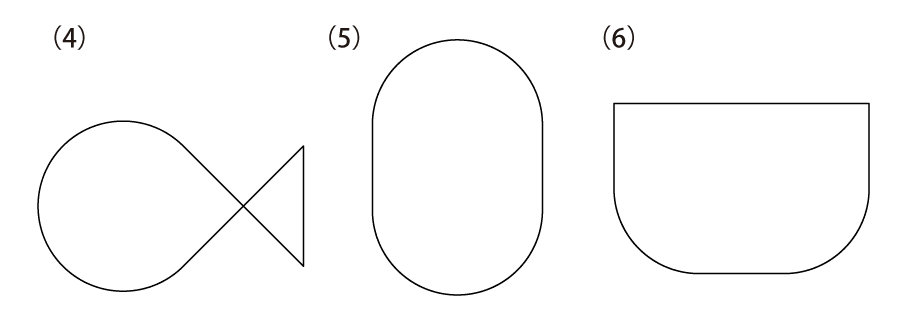
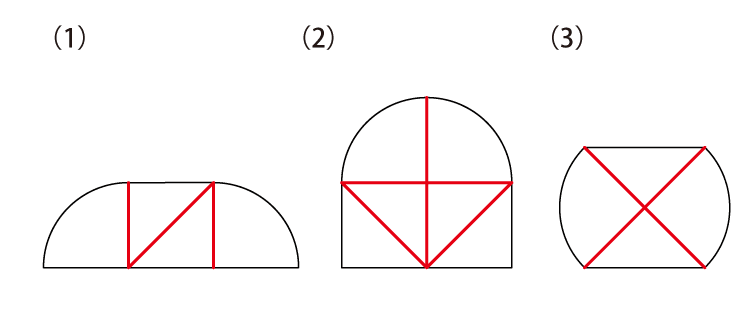
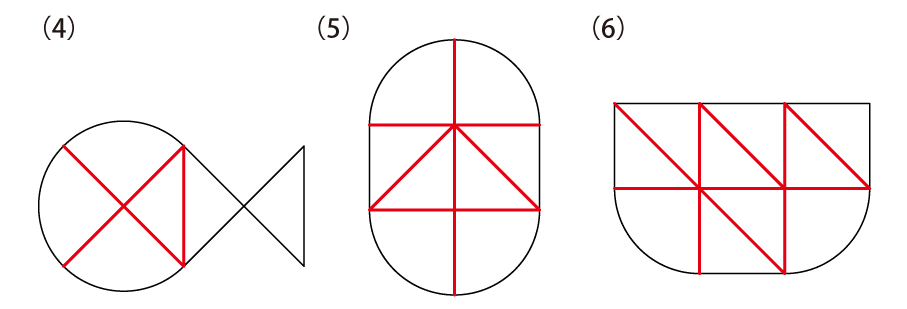
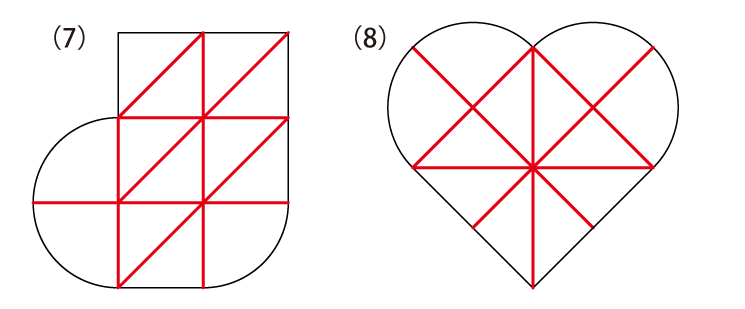
算数で学習する分野の中で、やはり“図形”は悩まされる人も多い分野のひとつではあるでしょう。確かに、図形の問題は「考えてもわからない」気がするものも多く、ともすれば“センス”が必要なのではないか、と思ってしまうこともありますね。実際、“図形のセンス”というものは存在し、それが必要な場面も確かにあります。ただ、この“センス”という言葉の扱いには慎重にならなければいけません。何かしらの“才能”や“特殊能力”のようなものを想定し、「それがないから自分には（子どもには）無理かも」と諦めてしまうのであれば、それは違う、というのを強く主張しておく必要があるでしょう。

“センス”という言葉をフラットに受け止めるのであれば、それは「感覚」でしかありません。“図形のセンス”と言った場合は、「図形の特徴を感覚的にとらえる力」のことを指していると考えればいいでしょう。つまり、図形のセンスを身につけるというのは、ざっくりと言えば「図形の特徴を（感覚的に）とらえられるようになる」ということなのです。

そもそも、算数の学習で“図形”を学ぶ目的も、「図形の特徴を理解する」ということですよね。その意味では、「図形のセンスを身につける」ことと「算数の学習をする」ことに、本質的な違いはありません。もちろん、それが“感覚的かどうか”というところには、少し違いがあるでしょう。算数を学習する意義のひとつとして、「感覚的にとらえているものを、意識化・言語化できるようになる」というものがあります。“なんとなく”わかっていることを、意識的に理解したり言語化してとらえたりすることで、“しっかり”理解していくのが「算数の学習」です。そう考えると、むしろ“センス”よりも“算数の学習”の方が大事な気はしてきますね。

図形を学ぶ上で“センス”が必要な気がする、と感じる人が多いのは事実なのでしょう。ただそれは、単純に「図形の学習」がそもそも難しいから、というのが大きな原因のひとつとなっています。図形の特徴を捉える、と言っても、「理解しておきたい図形の特徴」というのが、とても多いのです。正方形ひとつとってもそうですね。「すべての辺の長さが同じ」というのはもちろんそうですが、それ以外にも「すべての角の大きさが同じ（直角）」や「対角線の長さが同じ」など、理解しておきたい特徴がたくさんあります。それらをひとつでも多く言語化し、理解していく、というのが算数の学習ですが、実際にはそこまですべてすぐに理解するのはなかなか難しいでしょう。その点において、「感覚的な“理解”のサポートがあった方が、学習がスムーズに進めやすい」というのは事実です。

図形のセンスを身につけるためには算数の学習をすればいいのですが、その“算数の学習”をいわゆる座学に限る必要はないでしょう。実際に図形を触ってみて、動かしてみて、その体験の中から「図形の特徴を学ぶ」ということも、立派な算数の学習のひとつです。もちろん、最終目標は言語化して自分の中に落とし込むところではありますが、それはとても高いハードルです。焦る必要はありませんので、まずは感覚的にでも、少しずつ図形の特徴をとらえられるようになるといいでしょう。

今回の問題でも、慣れていないとなかなかうまくは解けません。それは、まだまだ「直角二等辺三角形」や「扇形」などの特徴を理解しきれていないからです。その場合は、繰り返しお伝えしているように、それらを切り取って実際に並べてみるといいでしょう。どの辺が同じ長さなのか、どの角がきれいにくっつくのか、斜めにしたとき頂点の位置関係がどのようになるのか、そういったことを実物を見ながら確認していってほしい、というのが、今回の問題の狙いです。

いかがでしょうか。

年度の早い段階で誕生日を迎えると、新年度の慌ただしい時期にいつの間にか誕生日が終わってしまいますよね。思えば学校で新しい学年になったときなどでも、クラスが変わって人間関係が落ち着いて、誕生日の話題が出るようになった頃にはすでに過ぎている、というパターンはありました。新しい歳の抱負を語るにしても、新年度ですでに語っていたりもして、そこからそんなに変わっていないんだけど、とはなりますね。ちなみに私の○○歳の目標は、「人間ドックに行く」です。まあ先月、今年度の目標を「健康に気を使う」としたので、その一環です。旅行も兼ねて泊まりがけでのんびりと行くプランもあるらしく、そういうのもありだな、と思っている今日この頃です。

それではまた来月！