さんすう力を高めるにはどうしたらいいの? まあ、そんなに難しく考えないで、まずはお子さまと一緒に問題に取り組んでみましょうよ。
(執筆:小田敏弘先生/数理学習研究所所長)
※本記事は、2023年7月27日に「Z-SQUARE」上で掲載した記事を一部修正の上、再掲しています。

さんすう力を高めるにはどうしたらいいの? まあ、そんなに難しく考えないで、まずはお子さまと一緒に問題に取り組んでみましょうよ。
(執筆:小田敏弘先生/数理学習研究所所長)
※本記事は、2023年7月27日に「Z-SQUARE」上で掲載した記事を一部修正の上、再掲しています。
![]() こんにちは、旅行に行く前にはいつも旅行雑誌を買ってしまう小田です。旅行雑誌を見ていると、ここも行きたい、あれも買いたい、と夢が広がり、わくわくしますよね。最近は、紙の書籍ではなく電子書籍で買うようにしているのですが、ぱらぱらと何気なくめくっていくには紙のほうがいいのかも、と感じていたりはします。とはいえ、電子書籍には「荷物が増えない」という最大のメリットがあるので、悩ましいところです。両方買うという選択肢も、なくはないですけどね。
こんにちは、旅行に行く前にはいつも旅行雑誌を買ってしまう小田です。旅行雑誌を見ていると、ここも行きたい、あれも買いたい、と夢が広がり、わくわくしますよね。最近は、紙の書籍ではなく電子書籍で買うようにしているのですが、ぱらぱらと何気なくめくっていくには紙のほうがいいのかも、と感じていたりはします。とはいえ、電子書籍には「荷物が増えない」という最大のメリットがあるので、悩ましいところです。両方買うという選択肢も、なくはないですけどね。
さて、今回は展開図を組み立てる問題です。あまり得意ではない、と感じている人も多いかもしれません。慣れていないと、難しいですよね。なかなかうまくいかない場合は、実際に展開図を用意して組み立ててみるといいでしょう。まずは「立体と触れ合う」ことを楽しんでみてください。
それでは早速行ってみましょう。
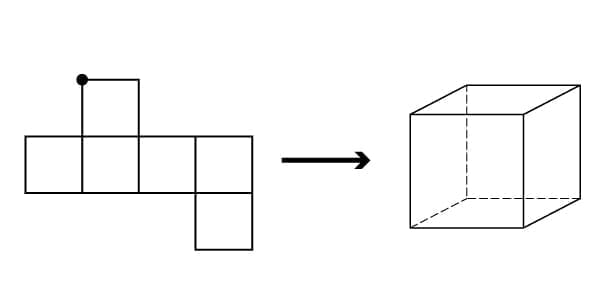
下の形を組み立てて、右のような立体を作ります。このとき、●の点とくっつく点はどれですか。いくつかある場合は、すべて選んでください。
下図の赤い●をつけた点
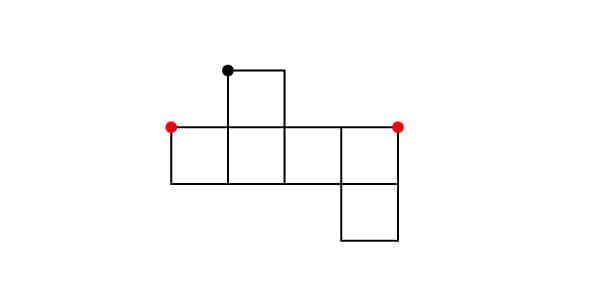
まずは問題の意味の確認ですね。答え方については、好きなように答えてもらって構いません。上に示したように、くっつく点に何かしら印をつける、という感じでもいいですし、その他、どの点を指しているかがわかる形であればそれで大丈夫です。
“右のような立体”とは「立方体」を指していますが、そもそも「立方体」がイメージできていない子には、「サイコロみたいな形だよ」と伝えてあげましょう。それでも難しいようなら、サイコロなど、立方体の形をしたものを実際に見せてあげてください。
展開図に慣れていない場合や、展開図を“組み立てる”の意味が怪しそうな場合、「くっつく点」の意味がわかっていなさそうな場合は、実際に展開図を用意してあげましょう。問題で聞かれている点以外のところで、「たとえばこことここは組み立てるとくっつくね」と示してあげてください。
問題の意味がわかった様子であれば、あとはしばらく見守ってあげましょう。お子さんが答えを出したら、その答えが正しいかどうかを伝えてあげます。2つのうち1つしか見つけていない場合は、「他にもあるよ」と伝えてあげてください。何回か間違えたり、なかなか答えが出せなかったりする場合は、やはり展開図を用意してあげましょう。正解していても自信がなさそうな場合は、「確認してみようか」という感じで、展開図を組み立ててもらって構いません。
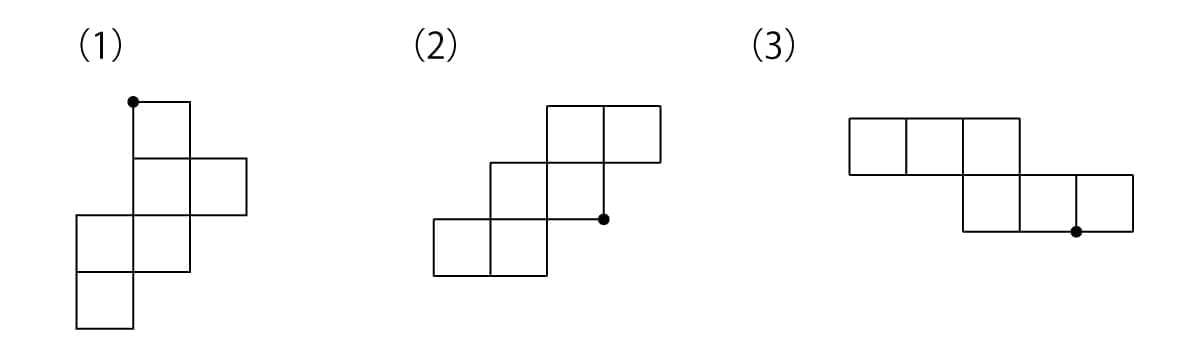
次の(1)(2)(3)の図を組み立てて、下のような形を作ります。このとき、●の点とくっつく点はどれですか。いくつかある場合は、すべて選んでください。

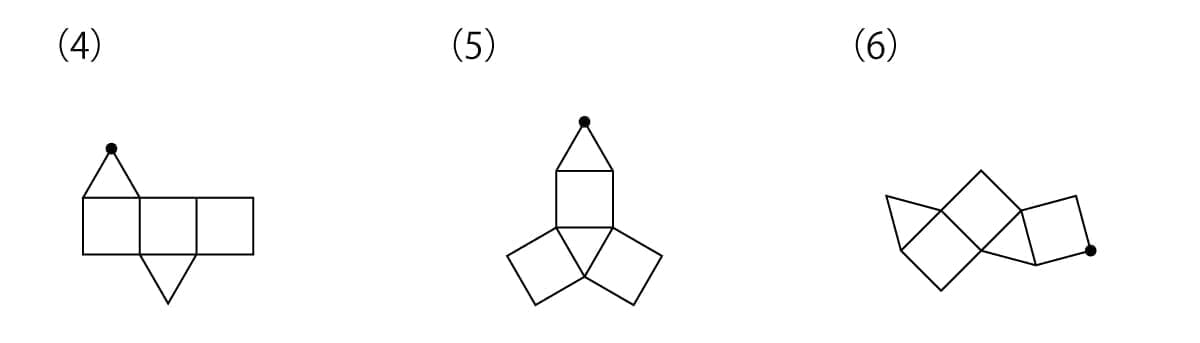
次の(4)(5)(6)の図を組み立てて、下のような形を作ります。このとき、●の点とくっつく点はどれですか。いくつかある場合は、すべて選んでください。

次の(7)(8)の図を組み立てて、下のような形を作ります。このとき、●の点とくっつく点はどれですか。いくつかある場合は、すべて選んでください

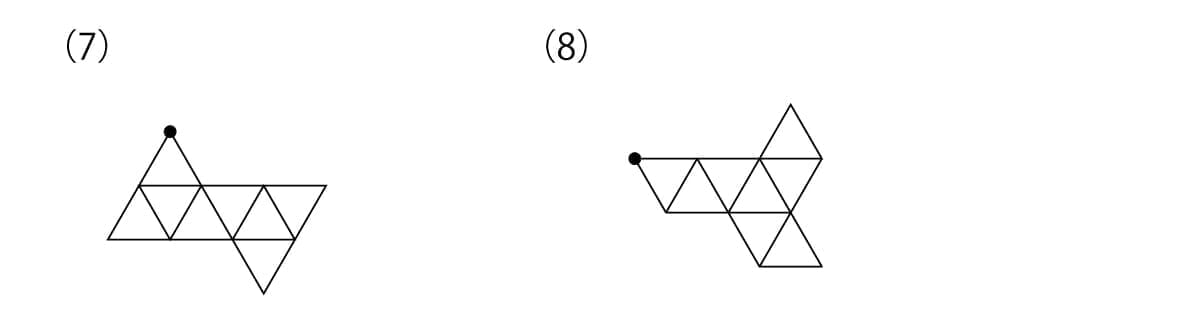
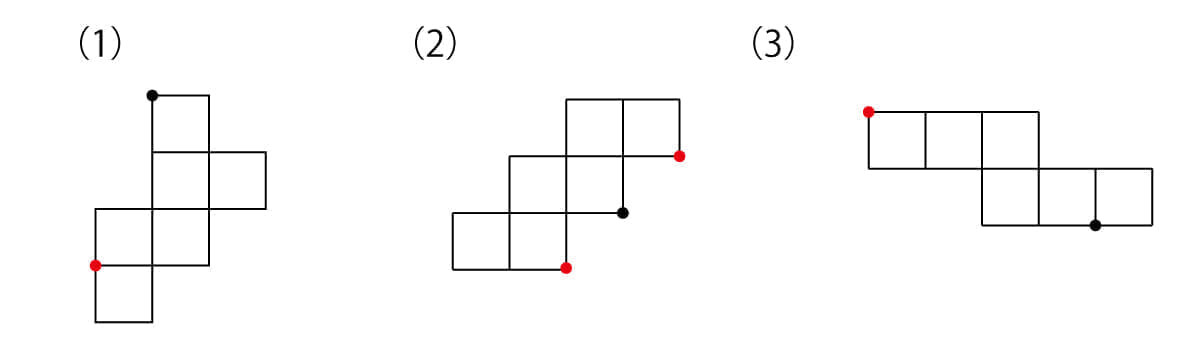
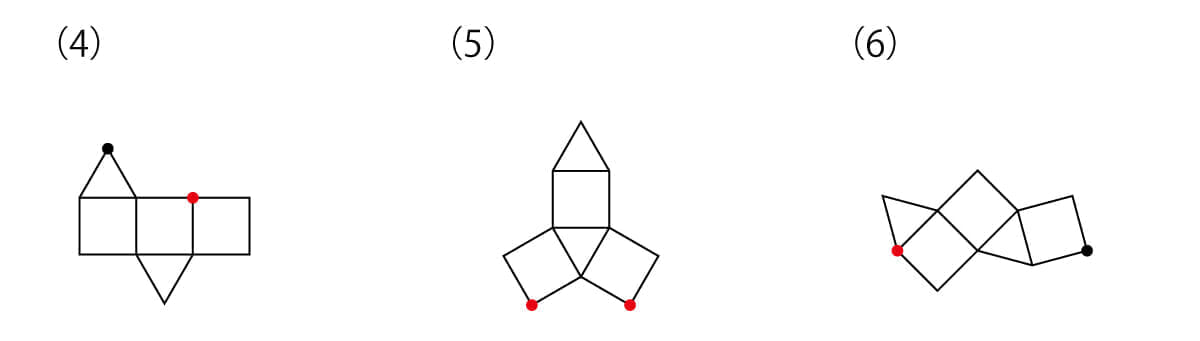
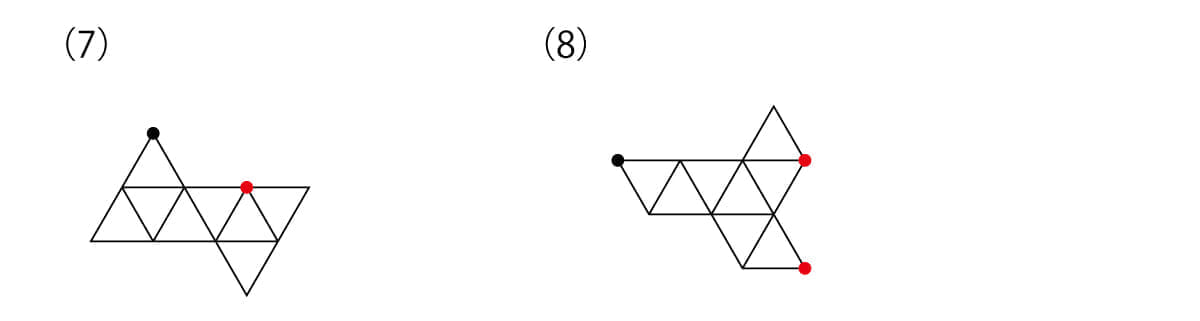
冒頭にも書いた通り、立体図形は“あまり得意ではない”と感じてしまう人が多い分野のひとつですね。ただ、6月号で“場合の数”のお話をしたときにもお伝えしましたが、立体図形についてもあまり“苦手”だとは思い込まないでほしい、というのは今回も改めてお伝えしておきます。やはり「立体図形をとらえていく」というのは、そもそも難しいことなのです。あまりうまくとらえられなかったとしても、それは“苦手”なのではなく、それが“普通”であると言えるでしょう。
図形の学習は難しい、というお話は、5月号でもお伝えしましたね。5月号では平面図形についてお伝えしましたが、立体図形はさらに難しいです。とはいえもちろん、学習の目標は、平面図形でも立体図形でも本質的には変わりません。ゴールはやはり「図形の特徴を理解する」ということです。そのために大事なことは、「立体図形と仲良くなること」や「図形の特徴を言語化して理解すること」なのです。
今回の問題で、例題やLevel 1のような「立方体(サイコロの形)」くらいなら、実際に見たことがある・触ったことがある人も少なくないでしょう。しかし、Level 2の「三角柱」や、さらにLevel 3の「正八面体」となってくると、実物を見たことがない人も多いのではないでしょうか。もし、お子さんにこの問題に取り組んでもらったとき、こういった図形を実際に見たことがあまりない様子でしたら、まずはぜひ実物を見せてあげてください。今回の展開図を切り取って組み立てて作ってみてもいいですが、その他、折り紙で作ったりすることもできますし、そのまま立体が市販されていたりすることもあります。興味のある方は調べてみてください。
“完成形”と慣れ親しんだら、次は「展開図を組み立てる」ことにも慣れていくといいでしょう。「展開図を組み立てる」作業も、なかなか日常の中で経験していることが少ないかもしれません。問題の画像を印刷して切り取ってあげてください。こちらも、知育玩具として市販されているものがいくつかありますので、興味のある方はそちらも調べてみるといいでしょう。
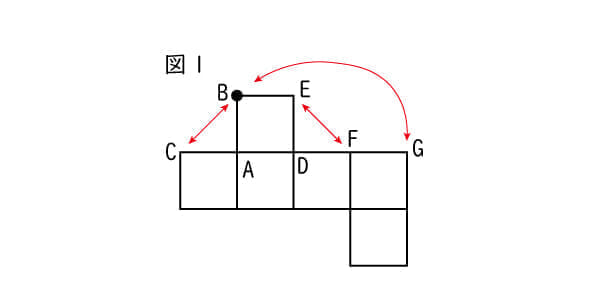
ある程度、「作る形」や「組み立てる」という作業に慣れてきたら、頭の中でも再現できるように練習していきたいですね。その際には、「細部を言語化していく」ことが大事になります。たとえば、「隣の点を順にくっつけていく」などのアプローチがあるでしょう。例題の展開図で、他のどの点ともくっつかない点A(図1)に注目してみます。印のついた点(B)は、点Aの“隣の点”なので、同じく「点Aの隣」にある点Cとくっつきますね。同じように、点Dに注目すると、その隣にあたる点Eと点Fがくっつきます。点Bは点Eのさらに隣にあるので、点Fの隣の点Gともくっつくでしょう。そうやって、「どことどこがくっつくか」を順に考えていくと、答えにたどりつきやすいですね。ただし、この方法は面が多くなるとうまくいかないことがあります。面が多いと、途中で間に別の面が遠くから挟まってくることがあるからです。
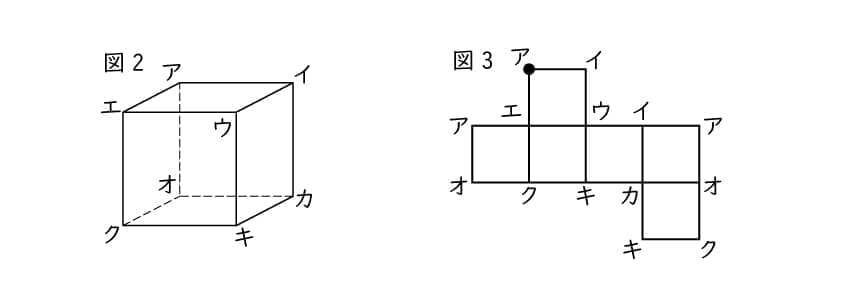
もうひとつ有効な手段として、「頂点に名前をつけてしまう」という方法もあります。図2のように立方体の頂点に、アからクという名前をつけてみましょう。そして、例題の展開図の印がついた面を「面アイウエ」として、印のついた頂点を「点ア」とします(図3)。そうすると、展開図上で面アイウエは隣の面と辺エウでくっついているので、隣の面は面エウキクとわかります。そうやって、順に頂点を展開図に書き込んでいくと、図3のようになるでしょう。ここまでくると、印をつけた点アは他の「点ア」と書かれた点とくっつく、というのがわかりますね。
他にもいくつか“考え方”はありますが、いずれにしても、図形の特徴や細部の様子・パーツを言語化していく、という“視点”も、ぜひ学習していってほしいことのひとつです。
繰り返しになりますが、立体図形の学習は、そもそも難しいことなのです。“苦手”と思い込む前に、まずは立体図形と触れ合う時間を増やし、それらの形とぜひ仲良くなってほしいと思います。
![]() いかがでしょうか。立体図形の話をするときにいつも思い出すのは、私の幼稚園時代の思い出です。私がまだまだ幼かった頃、幼稚園の先生のことが大好きで、「折り紙を教えてもらう」ことを口実にして、暇さえあれば職員室に先生に会いに行ったりしていました。そのときに教えてもらったのが、いくつかパーツを組み立てて作る立方体でした。そのおかげで図形が得意になり、算数も好きになったことにしているのですが、まあ実際のところはどうなんでしょうね。いずれにしても、素敵な先生に恵まれていたのだと思います。
いかがでしょうか。立体図形の話をするときにいつも思い出すのは、私の幼稚園時代の思い出です。私がまだまだ幼かった頃、幼稚園の先生のことが大好きで、「折り紙を教えてもらう」ことを口実にして、暇さえあれば職員室に先生に会いに行ったりしていました。そのときに教えてもらったのが、いくつかパーツを組み立てて作る立方体でした。そのおかげで図形が得意になり、算数も好きになったことにしているのですが、まあ実際のところはどうなんでしょうね。いずれにしても、素敵な先生に恵まれていたのだと思います。
それではまた来月!

文:小田 敏弘(おだ・としひろ)
数理学習研究所所長。灘中学・高等学校、東京大学教育学部総合教育科学科卒。子どものころから算数・数学が得意で、算数オリンピックなどで活躍。現在は、「多様な算数・数学の学習ニーズの奥に共通している“本質的な数理学習”」を追究し、それを提供すべく、幅広い活動を展開している(小学生から大人までを対象にした算数・数学指導、執筆活動、教材開発、問題作成など)。
公式サイト:http://kurotake.net/
主な著書