さんすう力を高めるにはどうしたらいいの？ まあ、そんなに難しく考えないで、まずはお子さまと一緒に問題に取り組んでみましょうよ。
（執筆：小田敏弘先生／数理学習研究所所長）
こんにちは、冷凍したご飯の解凍に悩む小田です。先月、レンジを買い替えた話をしましたが、あれ以来、冷凍ご飯の解凍がうまくいかず、試行錯誤しているところです。買い替える前のレンジが壊れかけだったので、そのときと同じ時間設定にすると温めすぎで固くなってしまう、というところまではつきとめました。あとは、ターンテーブルの方がフラット式よりバランスよく解凍できる、とかはあるのでしょうか。引き続き、いろいろ調べたり試行錯誤したり、“勉強”していこうと思います。
さて今回は、図形のパズルです。5月号と同じく、決められたパネルを使って形を作る問題ですね。5月号でもお伝えしたように、難しそうであれば、実際に並べてみればいいでしょう。まずは気軽にチャレンジしてみてください。
それでは、さっそく行ってみましょう。
Stage56：図形と仲良くなろう
例題
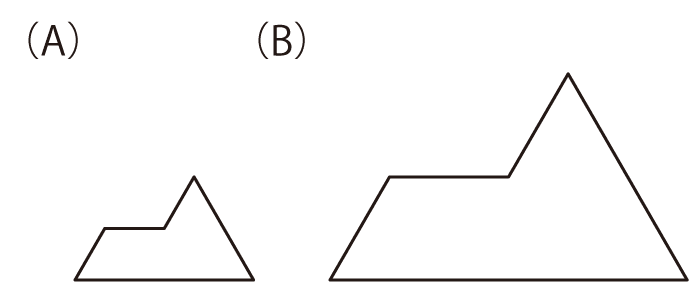
(A)の形のパネルを4枚使って、(B)の形を作ってください。パネルは、裏返したり回転させたりして使っても構いません。
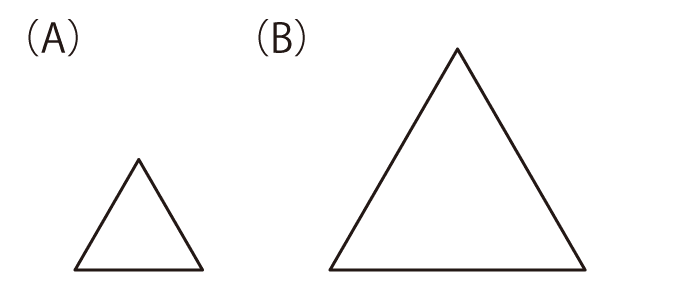
例題の答え
問題の意味は大丈夫だと思います。5月号と基本的には同じですね。いつも通り、まずは温かく見守ってあげましょう。答えはBの形の中に書き込んでもらってください。「解いてみよう」では、Aのパネルを裏返して使う問題もあります。それを忘れて苦戦しているようでしたら、「裏返しても使ってもいいよ」というのは伝えてあげてください。
5月号のときも難しかったと思いますが、今回はさらに難しいです。いきづまっている様子でしたら、ぜひ実際に“パネル”を作ってあげてください。今回はとくに「問題を解けること」よりも「形そのものを楽しむこと」を大事にしてほしいので、どうしても難しそうなら、最終的には答えを見せてあげても大丈夫です。お子さんが自分で答えを書いた場合は、あまりきれいに書けていなくても、だいたいあっていれば正解にしてあげてください。
解いてみよう
それぞれ (A)の形のパネルを4枚使って、(B)の形を作ってください。パネルは、裏返したり回転させたりして使っても構いません。
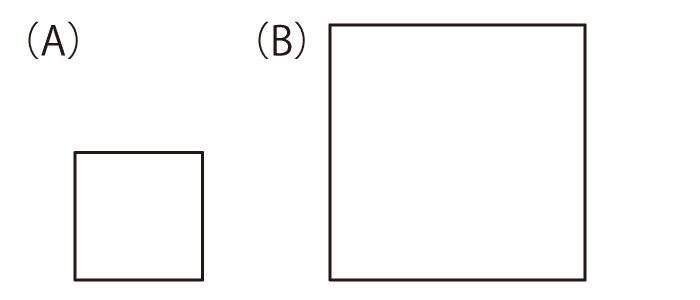
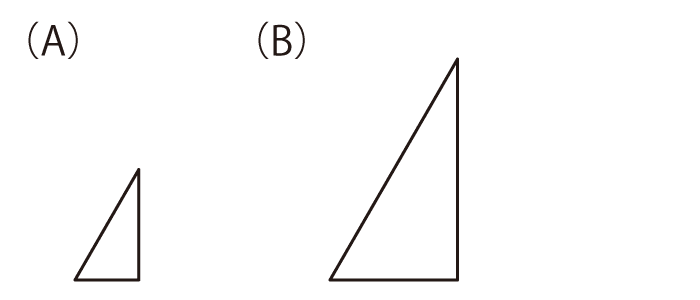
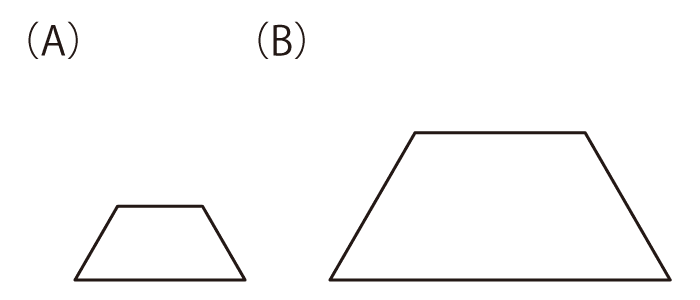
それぞれ(A)の形のパネルを4枚使って、(B)の形を作ってください。パネルは、裏返したり回転させたりして使っても構いません。
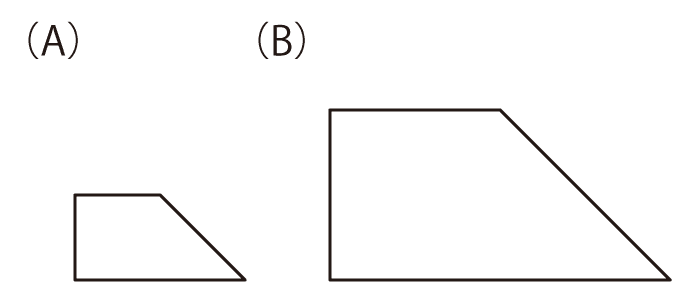
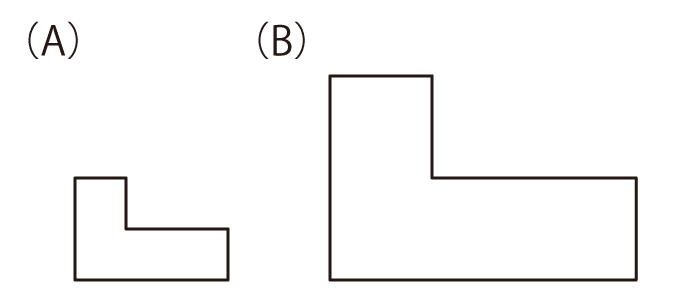
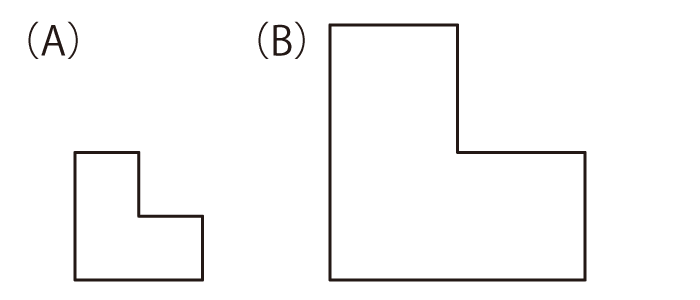
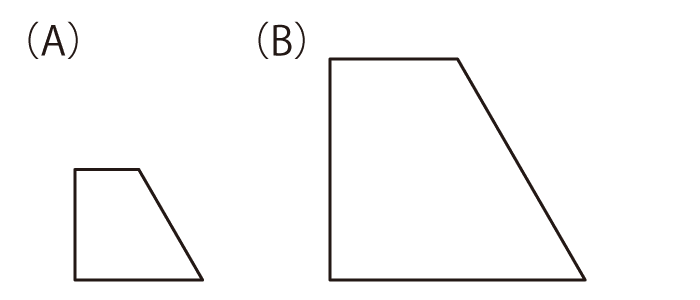
それぞれ (A)の形のパネルを4枚使って、(B)の形を作ってください。パネルは、裏返したり回転させたりして使っても構いません。
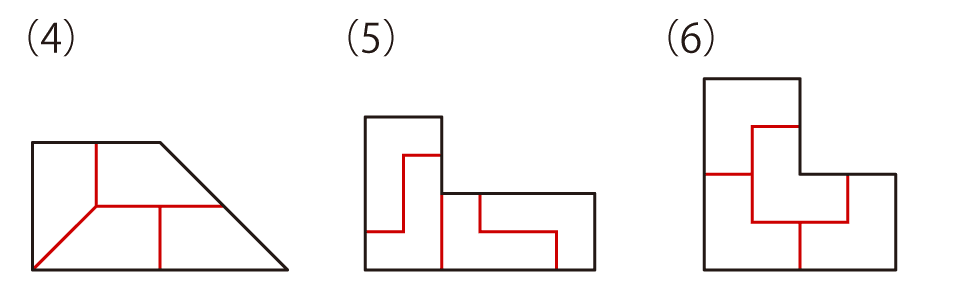
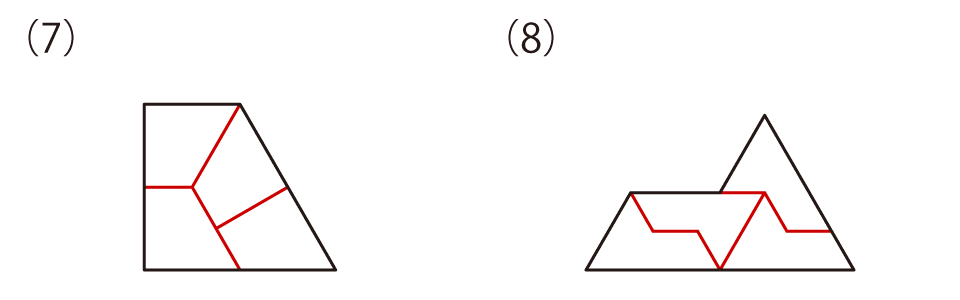
解答（例）
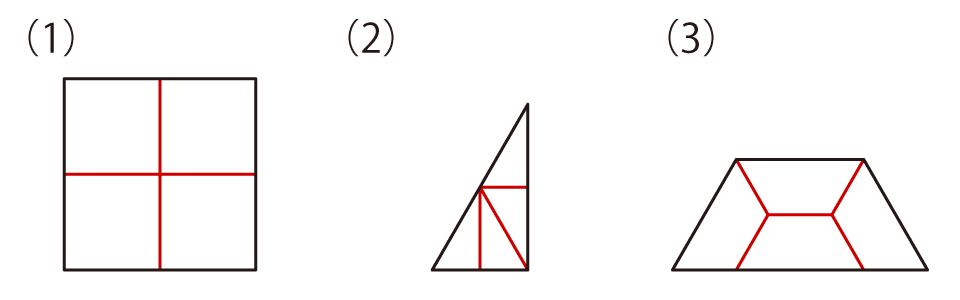
さんすう力UPのポイント
今回の問題、実際に形を作っていく中で、何か気づいたことはありますか。そうですね、作りたい形（Bの形）とそれを作るためのパネルの形（Aの形）は、大きさが違うだけで、形が同じですね。こういった、「同じ形をいくつか組み合わせると、ひとまわり大きな“同じ形”になる」ものを「レプタイル(rep-tile)」といいます。繰り返しの意味のrepeatとタイル(tile)から造られた言葉です（余談ですが、爬虫類も英語でレプタイルなので、“レプタイル”で検索すると爬虫類関連のものばかり出てきてしまいます。調べるときは、アルファベットで“rep-tile”と間にハイフンを入れて検索するのがいいでしょう）。今回は、4枚でできるものをそろえてみましたが、それ以外の枚数で“同じ形”になるものもあります。また、今回4枚で作った形の中にも、枚数を増やしてさらにひとまわり大きな“同じ形”が作れるものがあります。例題の形や（1）の形などは9枚でもできますが、これらは比較的わかりやすいですね。ほかにも、（8）の形が9枚でできたりするのですが、これは難しいかもしれません。ここでは答えは示しませんが、気になる人はぜひ挑戦してみてください。
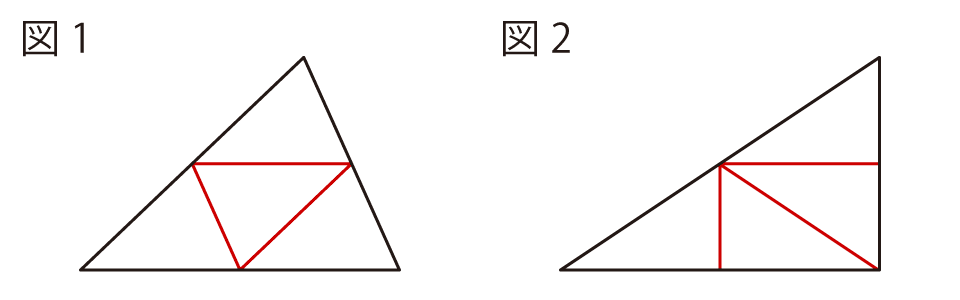
5月号などで、図形のセンスを身につけるためには、図形と仲良くなることが大事、とお伝えしましたね。今回の問題も、やはり「図形と仲良くなる」ことが一番の目的です。いろいろな図形を見ていると、興味深い性質をもつ図形のグループがいくつかあることに気づきます。“レプタイル”もそのひとつでしょう。そういった性質をどこまでおもしろがれるかというのは、結局のところ本人の趣味の問題なので、「おもしろがれることが図形のセンス」みたいなことは言いませんが、ただ単純にそういった図形と触れ合う時間の積み重ねが「図形のセンス」の基盤になっていることは間違いありません。まずは、「へぇ、そんな形もあるんだ」と知ることに、十分な価値があるでしょう。何度も繰り返し触れ合う中で、「ほかにもそういう図形がないかな」と気になってくると、さらにいいですね。そういった図形もある、という視点でいろいろな形と触れ合ってみると、例えば三角形は一般的にレプタイルになっていることに気づきます。図1のような並べ方をすれば、どんな三角形でもひとまわり大きな同じ形を作ることができますね。さらに突き詰めていくと、三角形の中でも直角三角形については、図2のような並べ方でも同じ形を作ることができる、ということに気づくかもしれません。
そうやって、同じ形を作れる形とそうでない形、同じ図形の作り方や枚数の違いなどを見ていく中で、さまざまな“図形”の特徴の理解を深めていけるといいでしょう。ぜひ、奥深い図形の世界を、楽しく探検してほしいと思います。
いかがでしょうか。
ふるさと納税の返礼でお米が届くことになっていたのですが、ストックの切れるタイミングにギリギリ間に合わず、普通に買ってしまいました。よくある話ではありますが、こういうときに限って自分で買った直後に届くものですよね。今回はさらに、株主優待のお米も届いたので、しばらくお米には困らなさそうな感じになりました。冷凍ご飯の解凍も研究しつつ、おいしく食べていきたいと思います。
それではまた来月！
文：小田 敏弘（おだ・としひろ）
数理学習研究所所長。灘中学・高等学校、東京大学教育学部総合教育科学科卒。子どものころから算数・数学が得意で、算数オリンピックなどで活躍。現在は、「多様な算数・数学の学習ニーズの奥に共通している“本質的な数理学習”」を追究し、それを提供すべく、幅広い活動を展開している（小学生から大人までを対象にした算数・数学指導、執筆活動、教材開発、問題作成など）。
公式サイト：http://kurotake.net/
主な著書
- 「算数のセンス」の具体的な中身を知りたい方はこちら
『できる子供は知っている 本当の算数力』（日本実業出版社） - 試行錯誤しながら、計算や図形のセンスを鍛えたり、考える力を育んだりしたい方はこちら
『東大文の会式 東大脳さんすうドリル 基礎編』（幻冬舎）
『東大文の会式 東大脳さんすうドリル 計算編』（幻冬舎）
『東大文の会式 東大脳さんすうドリル 図形編』（幻冬舎）
『東大文の会式 東大脳さんすうドリル 論理・文章題編』（幻冬舎） - 中学入試の問題の内容や、その本質が気になる方はこちら
『本当はすごい小学算数』（日本実業出版社）