こんにちは、今年こそシュトーレンを食べてみたいと思っている小田です。クリスマスに向けて毎日少しずつ食べていく例のアレです。楽しそうではあるのですが、毎日少しずつ切り取っていくとなると、途中で面倒くさくなってしまいそうな気もしています。そうやってためらっているうちに、例年、いつの間にかシーズンが終わってしまうので、今年こそは早めに決断して挑戦してみたいと思います。

さて今回は、論理のパズルです。間違ったことを言っている人がいる、いわゆる「嘘つき」の問題ですね。たんに「条件に合うものを探せばいい」だけではないので、そのぶん、難しくはなってしまいますが、まずは気軽に挑戦してみてください。

それではさっそく行ってみましょう。

 

Stage57：論理の力を鍛えよう

例題

机の上に、数字の書かれたカードが1枚、裏返して置かれています。このカードに書かれている数は、1，2，3，4，5のいずれかです。このカードに書かれている数について、Aさん、Bさん、Cさんの3人は、次のように言いました。

　Aさん「カードに書かれている数は、1か4だよ」
　Bさん「カードに書かれている数は、2か3だよ」
　Cさん「カードに書かれている数は、3か5だよ」

3人のうち、1人だけ間違ったことを言っているとき、カードに書かれた数は何でしょうか。

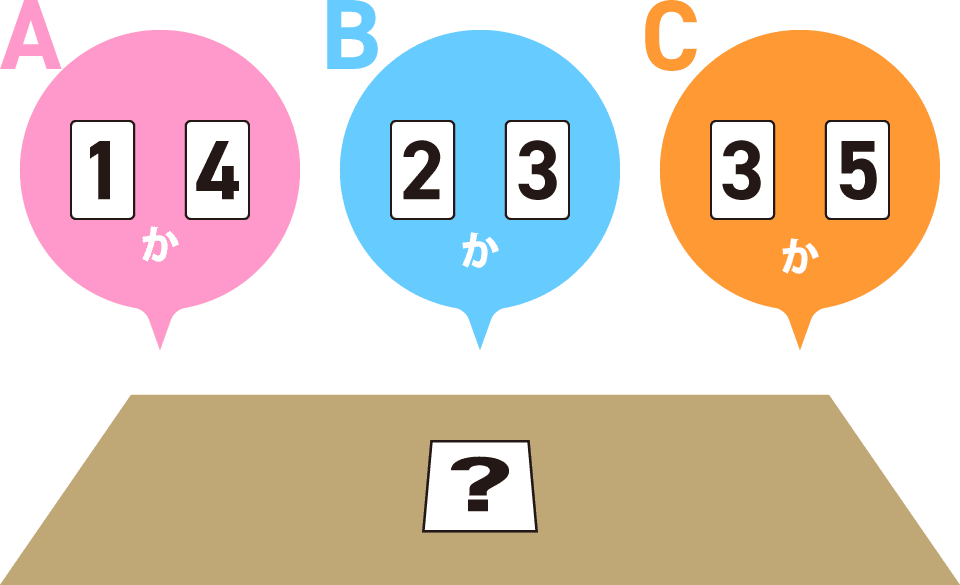
例題の答え

3 （間違ったことを言っているのはAさん）

まずは問題の意味の確認からですが、今回は「間違ったことを言っている」のところが、少し難しいかもしれません。意味がわかっていないようなら、「もし書かれた数が1だったら、Aさんの言っていることは正しいかな」と聞いてみましょう。Bさん、Cさんのセリフについても聞いてみて、「もし書かれた数が1だったら、3人のうち2人間違ったことを言っている」ことを確認してあげてください。問題の意味がわかっていても、どう考えていいかわからなさそうな場合は、同様に伝えてあげてください。

お子さまが自分なりに考え始められているようでしたら、いつも通り、温かく見守ってあげましょう。答えを出せたようなら、まずはその数について「カードに書かれた数が〇〇なら、Aさんの言っていることは正しいかな」と確認します。Bさん、Cさんについても確認し、「間違ったことを言っているのが1人だけ」となっていれば正解です。間違ったことを言っている人が2人になってしまっていたりしたら、「間違ったことを言っているのは1人だけだよ」と伝えてあげてください。

 

解いてみよう

（1）机の上に、数字の書かれたカードが1枚、裏返して置かれています。このカードに書かれている数は、1か2のどちらかです。このカードに書かれている数について、Aさん、Bさん、Cさんの3人は、次のように言いました。

　Aさん「カードに書かれている数は、1だよ」
　Bさん「カードに書かれている数は、2ではないよ」
　Cさん「カードに書かれている数は、2だよ」

3人のうち、1人だけ間違ったことを言っているとき、カードに書かれた数は何でしょうか。

（2）机の上に、数字の書かれたカードが1枚、裏返して置かれています。このカードに書かれている数は、1，2，3，4のいずれかです。このカードに書かれている数について、Aさん、Bさん、Cさん、Dさんの4人は、次のように言いました。

　Aさん「カードに書かれている数は、1か2だよ」
　Bさん「カードに書かれている数は、2か4だよ」
　Cさん「カードに書かれている数は、1か3だよ」
　Dさん「カードに書かれている数は、1ではないよ」

4人のうち、1人だけ間違ったことを言っているとき、カードに書かれた数は何でしょうか。

 

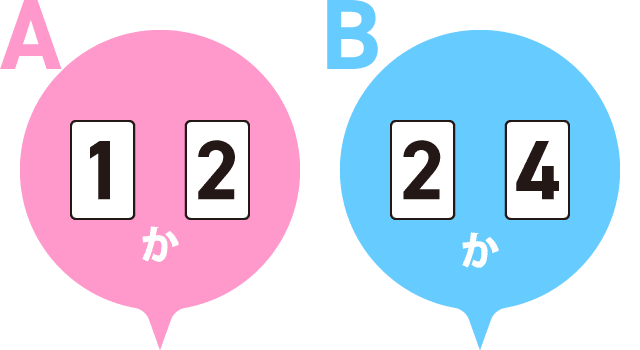
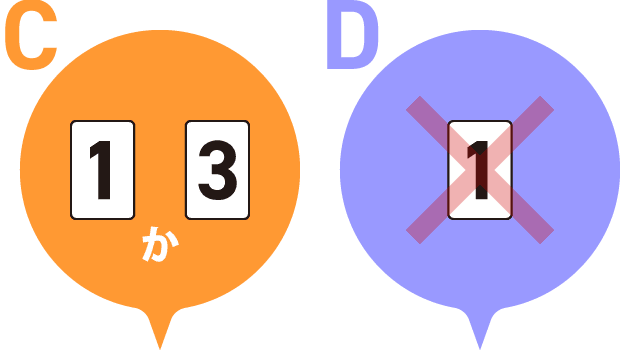
（3）机の上に、数字の書かれたカードが1枚、裏返して置かれています。このカードに書かれている数は、1，2，3，4，5のいずれかです。このカードに書かれている数について、Aさん、Bさん、Cさんの3人は、次のように言いました。

　Aさん「カードに書かれている数は、2か3か5だよ」
　Bさん「カードに書かれている数は、1か4か5だよ」
　Cさん「カードに書かれている数は、3より大きいよ」

3人のうち、1人だけ間違ったことを言っているとき、カードに書かれた数は何でしょうか。

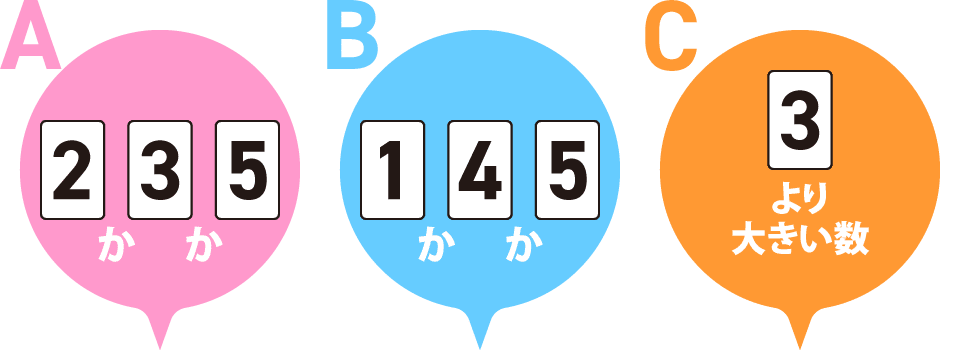
（4）机の上に、数字の書かれたカードが1枚、裏返して置かれています。このカードに書かれている数は、1，2，3，4，5，6のいずれかです。このカードに書かれている数について、Aさん、Bさん、Cさん、Dさんの4人は、次のように言いました。

　Aさん「カードに書かれている数は、1か3か6だよ」
　Bさん「カードに書かれている数は、3でも5でもないよ」
　Cさん「カードに書かれている数は、4より小さいよ」
　Dさん「カードに書かれている数は、奇数だよ」

4人のうち、1人だけ間違ったことを言っているとき、カードに書かれた数は何でしょうか。

 

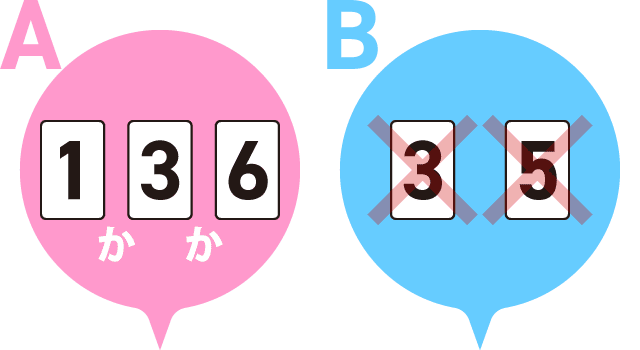
（5）机の上に、数字の書かれたカードが2枚、裏返して置かれています。これらのカードに書かれている数は、どちらも1，2，3，4，5のいずれかです。これらカードに書かれている数について、Aさん、Bさん、Cさんの3人は、次のように言いました。

　Aさん「カードに書かれている数をたすと、6になるよ」
　Bさん「カードに書かれている数のうち、大きい方から小さい方を引くと、3になるよ」
　Cさん「カードに書かれている数をかけると、8になるよ」

3人のうち、1人だけ間違ったことを言っているとき、カードに書かれた数は何でしょうか。

 

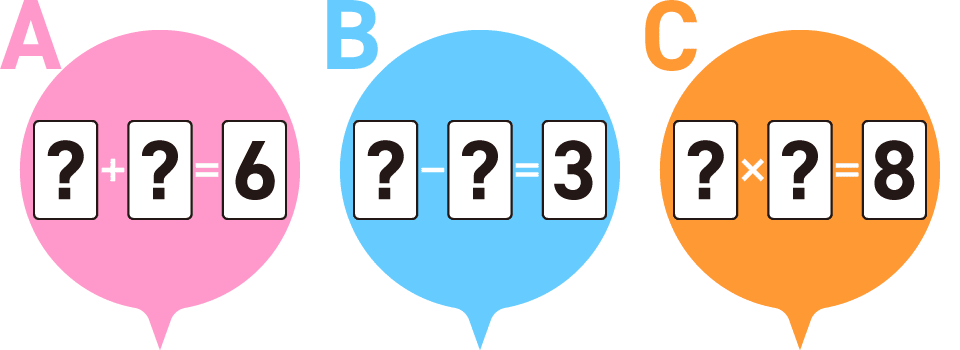
解答

（1）1（間違ったことを言っているのはCさん）
（2）2（間違ったことを言っているのはCさん）

 

（3）4（間違ったことを言っているのはAさん）
（4）3（間違ったことを言っているのはBさん）
※ 「3より大きい」「4より小さい」は、それぞれ「3」「4」を含まないことに注意してください。

 

（5）2と4（間違ったことを言っているのはBさん）

 

さんすう力UPのポイント

算数における「論理的思考」の話は、6月号や9月号でもお伝えしてきましたね。「結論の候補をあげて」いき、それぞれの候補に対して「条件をみたしているか確認」することで、「正しい結論」を導くことができる、ということでした。今回の問題でも、まずは「結論の候補」をいくつかに絞り込むことができますね。例えば、カードに書かれた数に注目すると、（1）なら「1」か「2」のいずれかしかありません。「もしカードの数が1だったら」と考えると、AさんとBさんは正しいことを言っていて、Cさんが間違ったことを言っている、ということになります。これは「3人のうち、1人だけ間違ったことを言っている」という条件にあてはまっていますね。一方で、「もしカードの数が2だったら」と考えると、Cさんは正しいことを言っていることになりますが、AさんとBさんの2人が間違ったことを言っていることになってしまいます。これでは「3人のうち、1人だけ間違ったことを言っている」という条件にあてはまっていません。よって、書かれている数は「1」とわかり、間違ったことを言っているのはCさんだとわかります。「誰が間違ったことを言っているか」に注目する方法もあるでしょう。この場合、（1）であれば「Aさん」か「Bさん」か「Cさん」の3つに結論が絞られます。もしAさんが間違ったことを言っているとしたら、Bさんの発言とCさんの発言が正しいということになります。しかし、「2ではない」と「2である」が両方正しいというのはおかしいので、「Aさんが間違ったことを言っている」というのは「正しい結論ではない」とわかります。同じように考えていくと、もしCさんが間違ったことを言っているなら、カードの数が1であれば「1である」と「2ではない」が両方正しくなるので、これが「正しい結論」だとわかります。

今回のような問題では、もちろん「正しいと言えることを探していって、それを順につないで“正しい結論”にたどりつく」という考え方もあります。（1）なら、Bさんの「2ではない」とCさんの「2である」が両方とも正しいわけがない、ということに気づけば、「少なくともAさんが言っていることが正しいな」と決めていくことはできます。そこから、カードの数が1であることも決まるので、Cさんが間違ったことを言っている、とわかりますね。ただ、そうやって「正しいことをつないでいく」考え方を見たときに、「そもそもなぜそこに注目したの？」と感じることはありませんか。（1）の問題のように、あからさまに反対のことを言っていれば気づきやすいかもしれませんが、そうでない場合に、「どの条件から考え始めればいいかわからない」となることはよくあります。そういった場面であっても、「カードの数は1か2かのどちらかのはずだから、それぞれの場合でどうなるか考えてみよう」とすることができれば、「正しい結論」にたどり着くことはできるのです。

「論理的な思考」というと、「〇〇だから××で、××だから△△」というように、「順番に言えることをつないでいく」というイメージがあるかもしれません。それはそれで大事な考え方ではあるのですが、それだけではなく、「結論の候補をすべてあげて、それらを順に精査していく」という考え方も、今回のような問題を通して身につけていってほしいと思います。

 

---

いかがでしょうか。

急に寒くなりましたね。冷え性なので、冬場は毎年「冬眠したいなあ」と思いながらやり過ごしています。とくに足先が冷えるといろいろとやる気も減退してしまうので、なんとか足元を温めようと試行錯誤する毎日です。どこかにしまった足入れヒーターも、そろそろ探し出さなければいけませんね。今年はそれに加えて、温かそうな室内用の靴下も買ったので、それらでなんとか乗り切っていきたいと思います。

それではまた来月！

 

「小田先生のさんすう力UP教室」の記事一覧はこちら