さんすう力を高めるにはどうしたらいいの？　まあ、そんなに難しく考えないで、まずはお子さまと一緒に問題に取り組んでみましょうよ。
（執筆：小田敏弘先生／数理学習研究所所長）

　こんにちは、先日ずいぶん久しぶりに蛍光灯を取り替えた小田です。最近の蛍光灯、ずいぶん長持ちするようになりましたよね。蛍光灯の交換は今の家に引っ越してきてから初めてで、予備の蛍光灯を用意していなかったので、あわてて電気屋さんに買いに行くことになりました。急だったので、ひとまず同じ蛍光灯を買ってきたのですが、そろそろLEDにしてもいいですよね。器具ごと付け替えないといけないので、めんどうそうではありますが。

さて今回は、数字のパズルです。大人から見ると、「これはわり算の問題かな」と思うかもしれませんが、お子さんにそれを伝える必要はありません。むしろ、「わり算」という先入観を持たない状態で、いろいろな試行錯誤を楽しんでほしいと思います。

それでは早速行ってみましょう。

Stage58：計算の意味を理解しよう

例題

次の式のA，Bは、それぞれ0から9までのうちのいずれかの数字を表しています。同じ記号は同じ数字、違う記号は違う数字を表しているとき、A，Bはそれぞれ何の数字を表していますか。

例題の答え

A：1、B：7

まずは、いつも通り問題の意味がわかっているかどうか、様子を見てあげるところからですね。いまいち問題の意味がわかっていなさそうな様子なら、「例えば、Aが1でBが2なら、12＋12で24になるね」と伝えてあげるといいでしょう。あとは、AとBにいろいろな数をあてはめてみるよう、うながしてあげてください。

数をあてはめ始めたら、あとは温かく見守ってあげてください。お子さんが答えを出したら、「たして34」になっているかどうかを確認します。なっていれば正解です。なっていなければ「○○＋〇〇だと××になるね」と伝えてあげてください。答え方は、「Aが1、Bが7」というふうに答えることを想定していますが、「17」と答えてももちろん大丈夫です。

繰り返しになりますが、お子さん自身がそうと気づかない限りは、「わり算」であることをあえて伝える必要はありません。お子さんが試行錯誤している様子を、温かく見守ってあげてください。

解いてみよう

Level 1

（1）次の式のA，Bは、それぞれ0から9までのうちのいずれかの数字を表しています。同じ記号は同じ数字、違う記号は違う数字を表しているとき、A，Bはそれぞれ何の数字を表していますか。

（2）次の式のA，Bは、それぞれ0から9までのうちのいずれかの数字を表しています。同じ記号は同じ数字、違う記号は違う数字を表しているとき、A，Bはそれぞれ何の数字を表していますか。

（3）次の式のA，Bは、それぞれ0から9までのうちのいずれかの数字を表しています。同じ記号は同じ数字、違う記号は違う数字を表しているとき、A，Bはそれぞれ何の数字を表していますか。

Level 2

（4）次の式のA，Bは、それぞれ0から9までのうちのいずれかの数字を表しています。同じ記号は同じ数字、違う記号は違う数字を表しているとき、A，Bはそれぞれ何の数字を表していますか。

（5）次の式のA，Bは、それぞれ0から9までのうちのいずれかの数字を表しています。同じ記号は同じ数字、違う記号は違う数字を表しているとき、A，Bはそれぞれ何の数字を表していますか。

（6）次の式のA，Bは、それぞれ0から9までのうちのいずれかの数字を表しています。同じ記号は同じ数字、違う記号は違う数字を表しているとき、A，Bはそれぞれ何の数字を表していますか。

Level 3

（7）次の式のA，B，Cは、それぞれ0から9までのうちのいずれかの数字を表しています。同じ記号は同じ数字、違う記号は違う数字を表しているとき、A，B，Cはそれぞれ何の数字を表していますか。

（8）次の式のA，B，Cは、それぞれ0から9までのうちのいずれかの数字を表しています。同じ記号は同じ数字、違う記号は違う数字を表しているとき、A，B，Cはそれぞれ何の数字を表していますか。

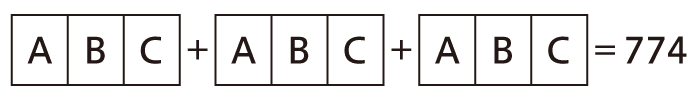
解答

Level 1　（1） A：2、B：3　（2） A：3、B：6　（3） A：7、B：8
Level 2　（4） A：1、B：3　（5） A：2、B：7　（6） A：4、B：6
Level 3　（7） A：1、B：9、C：2　（8） A：2、B：5、C：8

さんすう力UPのポイント

算数を学ぶ子どもたちを見ていると、「新しいことを学ぶ」のはそもそもとても難しいものだ、ということを痛感します。これは算数に限った話ではないと思いますが、「1回正しい方法・手順を伝えただけ」で、すぐに“正しくできる”ようになることは、なかなか少ないですよね。正直にいうと、そういった場面で、「それは前にも言ったでしょ」と思うことがないわけではありません。ただ、自分が“学ぶ”側に立ったときのことを思い返せば、「まあ確かに、1回聞いたくらいではわからないよな」と思い直したりはします。

「算数・数学を学ぶ」というのは、どういうことなのか。私はそれを、「自分の中にある“数学の庭”を育てる」ことだ、と表現しています。人はそれぞれ自分の中に“数学の庭”を持っています。算数・数学の学習を進めていく中で、新しく見つけたものをその庭に自由に置いていき、その庭を豊かにしていくのが「算数・数学を学ぶ」ということなのです。

新しいことを学んだとき、自分にとってしっくりくる“置き場所”があると、定着する確率が高くなります。逆に、新しいものをどこに置いていいかわからず、なんとなく“そのへん”に置いてしまうと、それは吹き飛ばされていつの間にかどこかに行ってしまうでしょう。いい置き場が見つからなければ、そもそも置けないこともあり得ます。そういった状況を外から見ると、「1回教えたのに覚えていない」となってしまうわけですね。

今回の問題は、突き詰めていけば「わり算」の問題です。しかし、わり算、とくにわり算の筆算は、初めて学習する子どもにとって、「いまいち何をやっているかわからないもの」のひとつです。よくよく考えると、たし算やひき算、かけ算の“筆算”とかたちが全然違うのも、不思議ですよね。計算の方法・手順だけ教わっても、何をやっているかよくわかっていなければ、なかなか定着しないでしょう。わり算の方法・手順を学習する前に、そのわり算の“イメージ”を作ってほしい、というのが、この問題のねらいです（その意味では、自分で「これはわり算だ」と気づいた子には、この問題はあまり意味のない問題ですが）。

わり算を知らなくても、わり算だと気づかなくても、たし算ができれば今回の問題を解くことはできるでしょう。いろいろやっていくうちに、大きさの見当をつけたくなってくるかもしれません。例題なら、もしAが2だと20+20で40となり、「大きすぎるな」となりますね。Aが1なら10+10で20なので、Aは1だろうとわかります。そうやって、「同じ数ずつに分けるために、位ごとに大きさの見当をつける」という経験をあらかじめ積んでいれば、わり算の筆算を学習した際にも、“やっていることの意味”がすんなり入ってくるでしょう。

「数学の庭」が豊かになればなるほど、新しく学んだことの“置き場”が増えていきます。手順を伝えることだけでなく、経験を積む機会を提供することで、その「数学の庭」を豊かにする手助けができるといいな、と思います。

いかがでしょうか。

いよいよ今年も終わってしまいますね。近年は、毎年のように「健康に気をつける」を目標にしているような気がしますが、なんだかんだでほどほどに元気に生きているので、一応目標は達成しているのでしょう。エアロバイクを定期的にこいだり、もずくを食べたり、食事のメニューを事前に決めたり、という習慣も、結構続いている気がします。来年は、もう少し運動量を増やしたいところではありますが。あと、人間ドックには、結局今年も行けずじまいだったので、来年こそは行けたらいいなと思います。

それではまた来月！

文：小田敏弘（大学教育学部総合教育科学科卒。子どものころから算数・数学が得意で、算数オリンピックなどで活躍。現在は、「多様な算数・数学の学習ニーズの奥に共通している“本質的な数理学習”」を追究し、それを提供すべく、幅広い活動を展開している（小学生から大人までを対象にした算数・数学指導、執筆活動、教材開発、問題作成など）。

公式サイト：http://kurotake.net/

主な著書