【解答】
5、53
【解説】
①1、2、12の3枚のカードで4桁の数を作るとき
カードの並べ方は、次のように6通りあります。
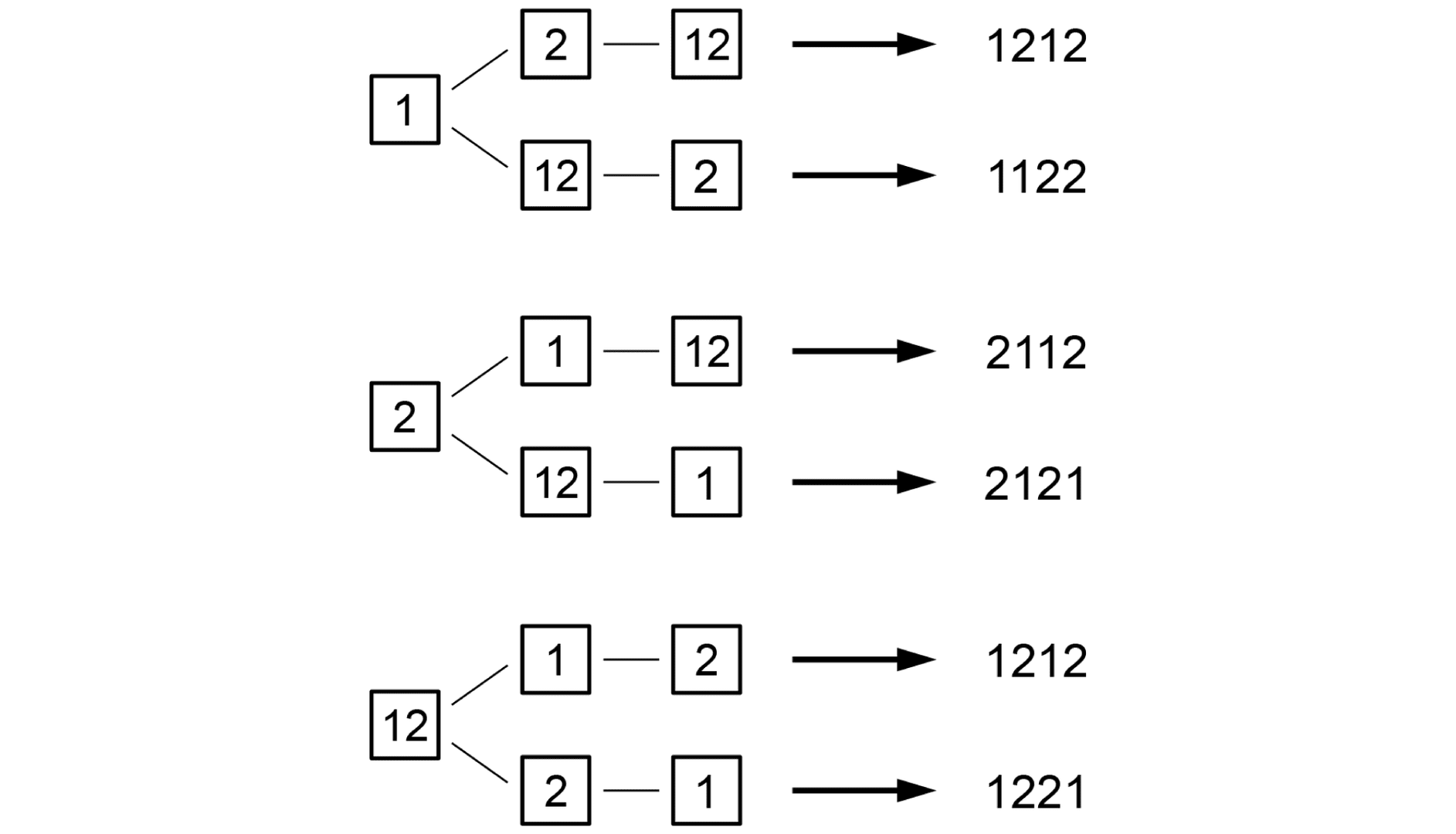
このうち、1212と1212はどちらも1212を表しているので、できる4桁の数は全部で5通りです。
②1、2、3、4、12の5枚のカードで4桁の数を作るとき
12のカードを使うかどうかで場合分けして考えます。(使うカードの枚数で場合分けすると考えても同じです。)
(ア)12のカードを使わない場合
1、2、3、4の4枚のカードを並べて4桁の数を作ります。たとえば千の位に1のカードを使うとき、下の図の6通りの並べ方があります。千の位が2、3、4の場合も同じように6通りずつあるので、できる4桁の数は、6×4=24(通り)です。
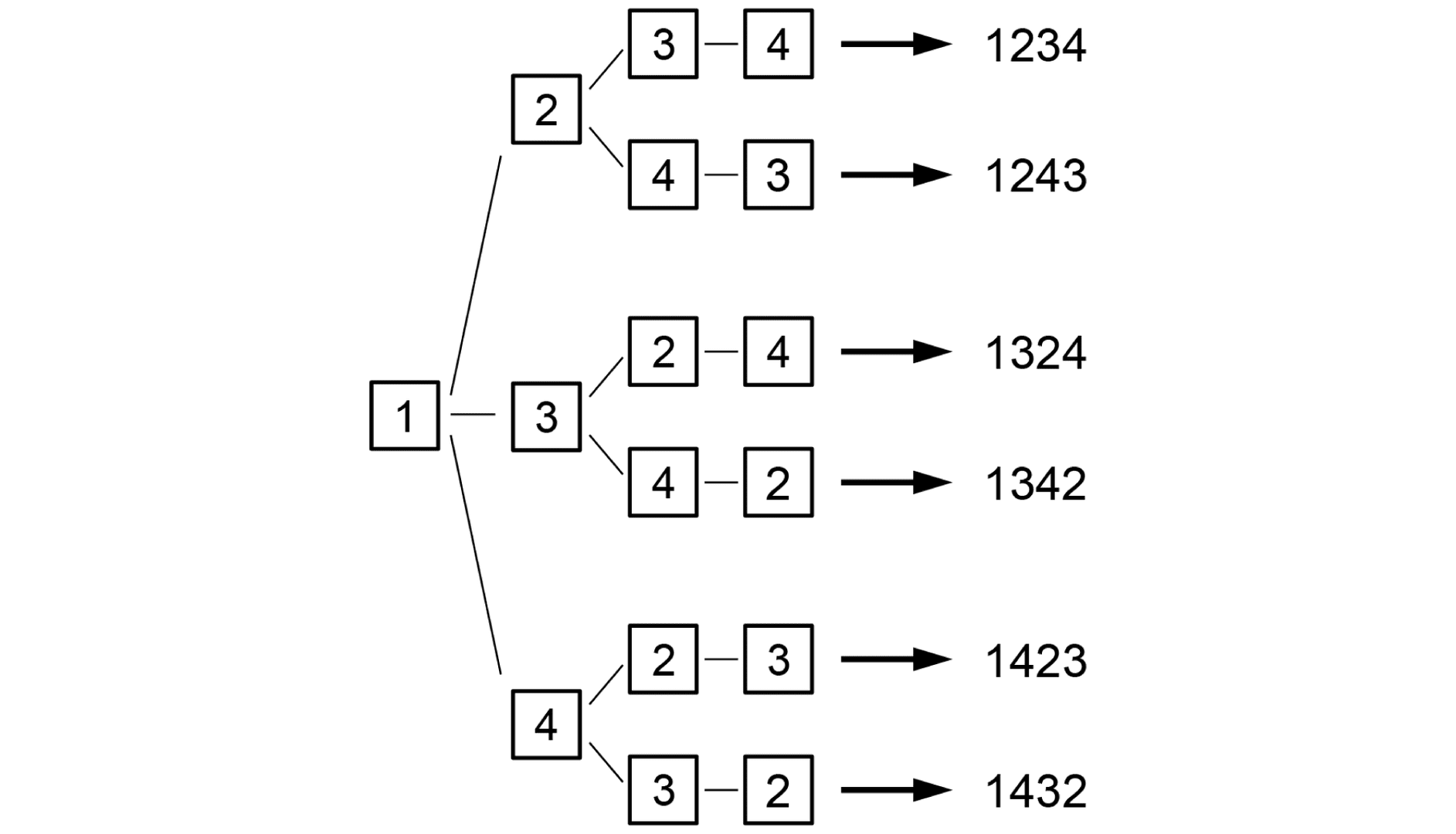
(イ)12のカードを使う場合
残り2枚のカードの選び方は、次の6通りがあります。
1 2 1 3 1 4
2 3 2 4 3 4
それぞれの場合で、①のときと同じように考えて6通りずつの並べ方があります。それぞれの並べ方でできる数に同じ4桁の数がないかを調べます。
●パターン1:1と2を使う場合
①で調べたように、5通りの数ができます。
●パターン2:3と4を使う場合
12、3、4の3枚のカードを並べるので、できる数は1、2、3、4の4つの数字を使ってできる数です。これらの数はすべて(ア)で数えているので、この場合は新しい数はできません。
●パターン3:パターン1・2以外の場合(4組あります)
①と同じように考えると、それぞれの場合で6通りの並べ方があるとわかります。この6通りの並べ方でできる数はすべて異なっています。
また、カードの選び方がちがうとき、4つの数字の組み合わせがちがうので、別のカードの選び方で同じ数ができることはありません。
(例)
12、1、3を選んだとき…数字の組み合わせは(1、1、2、3)
12、1、4を選んだとき…数字の組み合わせは(1、1、2、4)
したがって、全部で、6×4=24(通り)の数ができます。
以上から、12のカードを使う場合、(ア)でできる4桁の数とちがうものは、5+24=29(通り)できます。
(ア)、(イ)より、できる4桁の数は、24+29=53(通り)です。