こんにちは、年明け早々インフルエンザにかかった小田です。昨年同様、年末年始で2キロくらい体重が増えていたのですが、おかげさまで(？)すぐに元に戻りました。よかったのかどうなのか。ここ数年は毎年のように「健康に気をつける」ことを一年の目標にしている気もしますが、今年も変わらずそれでいいような気がします。体重はあと2〜3キロくらい減らせたらいいな、と思います。

さて今回は、図形の問題です。パズルというより、算数的な概念の理解につながる問題ですね。まずは気軽にチャレンジしてみてください。

それではさっそく行ってみましょう。

 

Stage59：図形の広さを考えよう

例題

図の（あ）の形は、（A）のパネル何枚分の広さでしょうか。

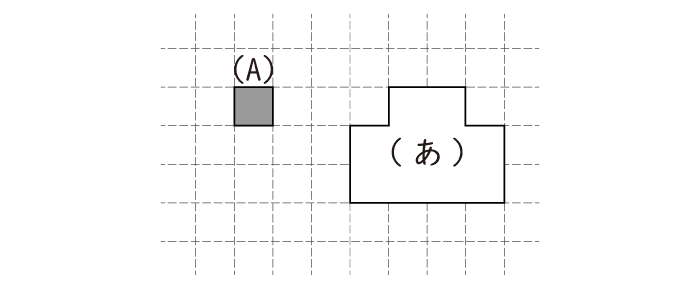
例題の答え

10枚分

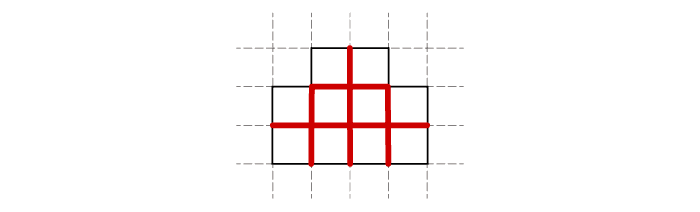
まずは問題の意味が理解できているかどうかの確認ですね。今回の問題は、「広さ」の概念がまだ身についていないお子さまには少し難しいと思いますので（とくに、Level2や3）、その場合は、無理に解こうとしなくても大丈夫です。「広さ」の概念って意外と難しいんだ、とご理解いただけるとうれしいです。

「広さ」がわかっていそうなら、まずはいつも通り温かく見守ってあげてください。上図のように線を引く、というのはひとつのヒントですが、お子さまが自分でやり出さない限り、いきなり伝える必要はありません。☐で埋めていこうとする考え方も大事ですね。大きさや形が安定しない場合は、大きめに印刷したものを切り取って、実際に「Aのパネル」を並べるのもいいでしょう。

 

解いてみよう

図の（1）（2）（3）の形は、それぞれ（A）のパネル何枚分の広さでしょうか。

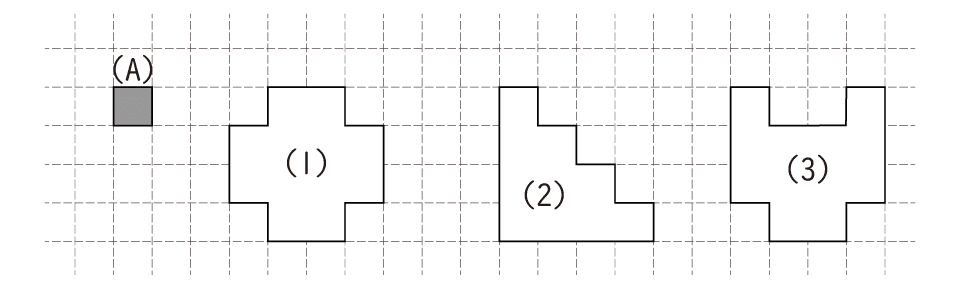
図の（4）（5）（6）の形は、それぞれ（A）のパネル何枚分の広さでしょうか。

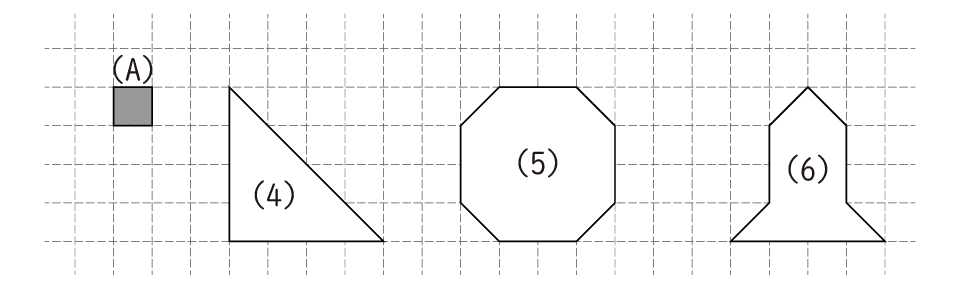
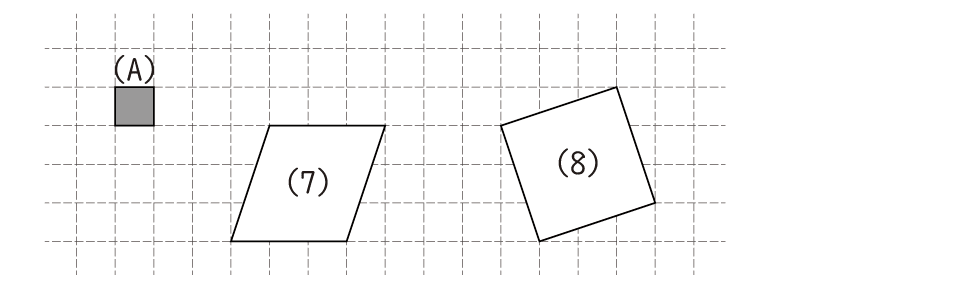
図の（7）（8）の形は、それぞれ（A）のパネル何枚分の広さでしょうか。

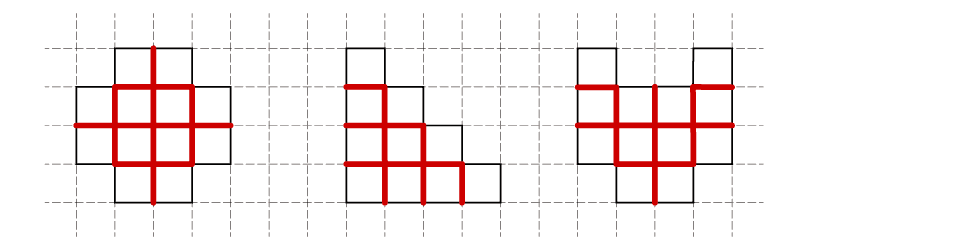
解答

（1）12枚分　（2）10枚分　（3）12枚分

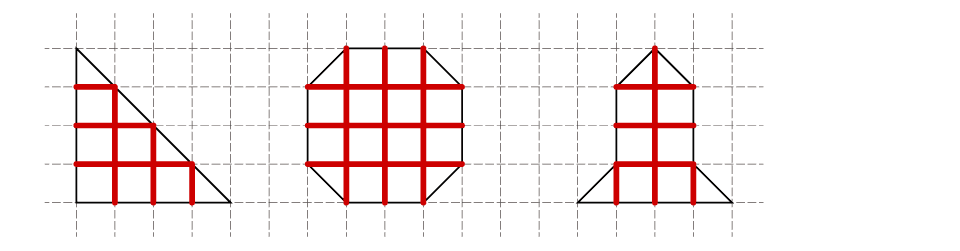
（4）8枚分　（5）14枚分　（6）8枚分

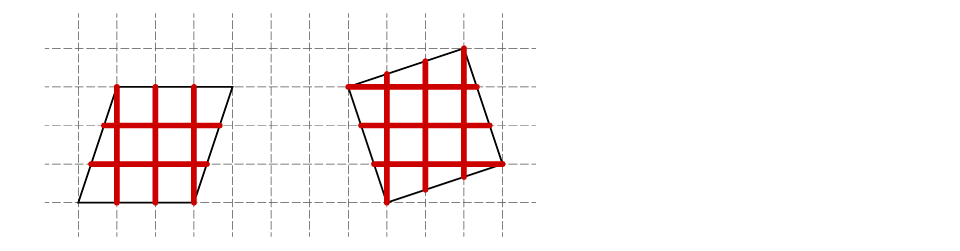
（7）9枚分　（8）10枚分

さんすう力UPのポイント

図の（あ）と（い）の形のうちどちらが“大きい”か、というのは、よくよく考えてみると、実はそう簡単な話ではありません。

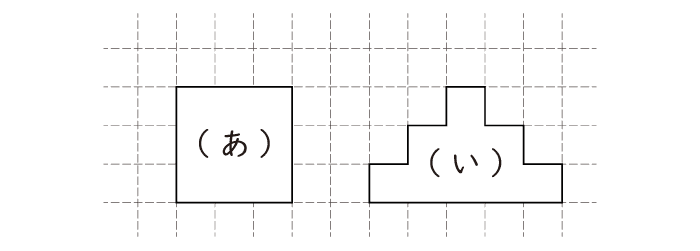
今回の問題と同じようにマス目の数を数えてみると、（あ）の形も（い）の形もともに9マスずつです。つまり、どちらも同じ“大きさ”のはずですね。しかし、子どもに考えてもらうと「（い）の方が“大きい”」と答えることがよくあります。子どもに限らず、なんとなく一見しただけだと、「（い）の方が“大きい”」と感じる人もいるかもしれません。ただ、それは別に「考えていない」というわけではないのです。

人がものの“大きさ”を判断するとき、注目している場所は1つではありません。算数で扱う概念で言うと、「長さ」「面積」「体積」「角度」などがそうですね。図形に関する量なので、まとめて「図形量」と呼ばれることもあります。ふだんの生活で何かを「大きい」と感じるとき、それが「どう大きい」のかは、そこまで意識してはいないでしょう。キリンも“大きい”ですし、ゾウも“大きい”ですね。しかし、つきつめて考えてみると、キリンの“大きさ”は「背の高さ（長さ）」についての評価ですし、ゾウの“大きさ”は「体積」についての評価です。個々のものをなんとなく“大きい”と感じるだけであれば、確かにどういう“大きさ”かまでを厳密にする必要はないでしょう。しかし、ほかのものと比べたりするときなど、基準を明確にする必要がある場面も存在します。「長さは長いけど、面積は大きくない」形や、「表面積は大きいけど、体積は大きくない」ものなど、いくらでもありますね。冒頭にあげた例も、「（あ）も（い）も面積は同じだけど、周りの長さは（い）の方が長い」ので、「（い）の方が“大きい”」と感じる人もいる、ということです。とはいえ、たんにそれらをまとめて“大きい”と言っているうちは、細かい議論を進めていくことができませんね。形や物の“大きさ”について理解を深めていくためには、何に注目した大きさなのかを区別できるようになる必要があるわけです。

こういった、「似ているけれども少し違うもの」を厳密に切り分けられるようになることこそ、算数の学習の意義のひとつです。算数に限った話でもありませんが、新しい概念を学ぶことで、“世界”に対する解像度をあげていく、というのが、「勉強をする」ことの重要な意義です。今まであまり区別をしてこなかったものを、きちんと分けられるようになっていくのは、結構難しいことではあるでしょう。実際、「長さ」と「面積」の区別や、「角度」と「面積」の区別は、引っかかりやすいポイントのひとつです。すでに区別ができるようになった人から見ると、「同じように見えていたころ」のことを覚えていないので、そういう子たちを見て、なぜ引っかかっているか、不思議に思うこともあるかもしれません。しかし、「例題の解説」でも触れたように、実際にはとても難しいことではあるので、そういったお子さまを見たときに、「難しいんだな」と理解してもらえるとうれしいと思います。

今回は、「図形量」の中でも「面積」のイメージを作っていく問題です。面積は、「1辺の長さが1である正方形」の何枚分か、を考えるところから始めます。いろいろな公式が出てきて混乱する前に、その根本的なイメージをしっかり作ってほしい、というのが、今回の問題のねらいです。

 

---

いかがでしょうか。

寒い日が続きますね。これまであまりインフルエンザなどにはかかったことがなかったので、自分でも少し驚いているところてはあります。ただまあ、確かに、歳を重ねるに従って、年々少しずつ無理は効かなくなってきたな、と感じることは事実です。毎年のように「健康に気を使う」と言っていますが、今年こそは少し生活リズムなども見直して行けたらいいなと思います。人間ドックも今年こそ行きたいですね。

それではまた来月！

 

「小田先生のさんすう力UP教室」の記事一覧はこちら