「お子さまに寄り添った添削」「充実した解説」を日々お届けしている通信教育のＺ会が、2025年度（2025年2月実施）開成中学校の入試問題「算数」を詳細に分析しました！
入試問題の概観と大問１つを厳選し、Ｚ会ならではの視点で解説をまとめましたので、ぜひお役立てください。
入試概観・解説（開成中学校）
開成中学校の算数を徹底分析！今年の入試問題の概観と、開成中ならではの問題「大問４」の詳細解説を掲載。
大問４の解説だけにとどまらず、今後の開成入試を解くときにも活かせる立体図形のポイントも紹介しますので、ぜひご確認ください。
概観
入試問題全体を通して
2023年度は大問5題、2024年度は大問3題の構成だったが、今年度は大問4題の構成。2024年度に続き大問1が小問集合形式となっている。過去の開成入試で見たことのある形式がいくつか見られ、過去問演習をしっかり行っている受験生には有利だっただろう。学校発表の合格者平均と全体平均によると、近年は開成の算数は10点程度差がつくことが多いが、今年度は8.3点の差にとどまった。点差がつかなかった（解きやすかった）であろう問題は大問１、大問２（１）（２）、大問４。点差がついた（難しかった）のは大問２（３）と大問３で、とくに大問３のグラフの扱いが明暗を分けたと思われる。
大問１
小問集合としては少なく2題。単位がついた式の計算問題と相当算だった。あっさりと解いて次へ進みたい。
大問２
独自のルールにしたがってポイントを計算する問題。（3）はポイントがなるべく大きい区切り方を1つ答えさせ、ポイントが大きい答えほど高い得点を与える形式。得点について問題文で言及する（なるべく～～な答えほど高い得点を与える）問題は2024年度の大問1（1）でも出題されている。ただし、2024年度の大問1（1）は得点が最も高い答えを見つけやすいものであったが、今年度の大問2（3）は最大になる区切り方が、たいへん考えづらい。あえて最大を狙わず、大きめの区切り方を見つけたらいったん見切りをつけ、他の問題に先に取り組んでいくのが戦略として有効だろう。
大問３
ダイヤグラムを用いた速さの問題。ただし2地点の間を3種類の経路を利用して往復するため、最初の状態（地点Aからアの道を通る状態）に戻るのは3回目に地点Aに着いたときである。
この周期性を考えやすくするために、ダイヤグラムは3の倍数（回目）に地点Aに着いたときで縦軸を用意しており、普段とはちがう表記方法にとまどった受験生も多かっただろう。このダイヤグラムでは地点Aや地点Bにあたる箇所が縦軸に複数あるところが難しいポイントではあるが、2024年度大問2でも見られた丁寧で細かく段階を踏んでくる誘導問形式になっている。それぞれの問題で問われている要素をきちんとおさえていければ決して解けない問題ではなかっただろう。
大問４
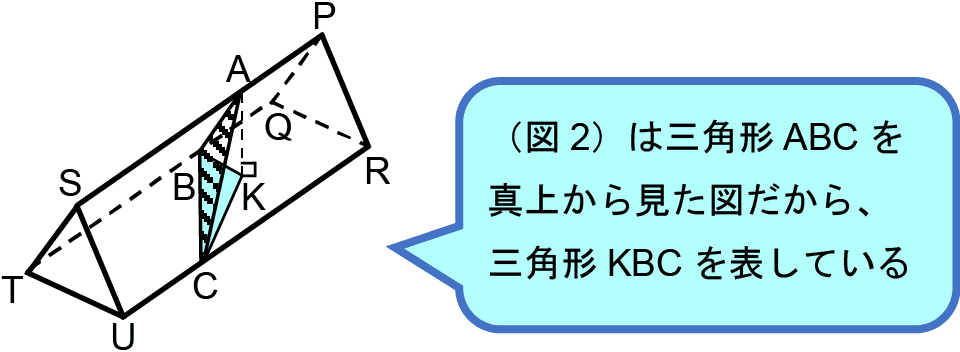
横に倒した正三角柱を切断し、切断面を真上から見たときのようすから、切断面の実際の形を考察する問題。切断面を真上や真横から見たときのようすから実際の形について考察するというテーマは、問われているものは違うが2019年度の大問2でも出題されている。また、2024年度大問3に続き図示の問題もある。最終的に扱われている内容は、立体の切断・投影図についての深い理解が必要な開成らしいものだったといえるだろう。（1）はヒカルさんが考察している長文を穴埋めしていく形式。難しい設定の問題について解法をほぼ明かした長文が用意され、穴埋めしていく問題形式は2023年度でも大問5の場合の数の問題で扱われている。今年度も問題文が導く通りに解けばつまることはないだろう。今後の開成入試でも扱われる可能性がある形式のため、出題されたときにとまどわないよう、この問題や2023年度大問5は一度解いておきたい。開成では立体図形、とくに切断の発展問題が非常によく出題される。『Ｚ会頻出分野別演習 立体図形難問対策』では、切断を含めたさまざまな立体図形の難問を、難関校の入試問題なども紹介しながら扱っているので、開成の立体図形対策としてぜひ取り組んでみてほしい。
大問４の解説
大問４「三角柱の切断面の考察」は、開成頻出の立体の切断と、開成で近年みられる長文の読解が組み合わさった問題だった。
大問４を解くだけであれば、長文の関係ある箇所を適宜拾っていけばいったんの正解を導き出すことができる。しかし、それではこの問題で考えていることの理解や今後の開成入試における立体図形対策としては不十分である。したがって、今回は大問４について、ヒカルさんの考察部分全体をふまえた広義の解説を行っていこうと思う。
（1）ア 90 イ 60 ウ 30 エ
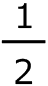オ 正 カ 3 キ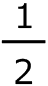 （2）以下解説に記載
（1）解説
（1）を解く前に、状況を確認しておこう。
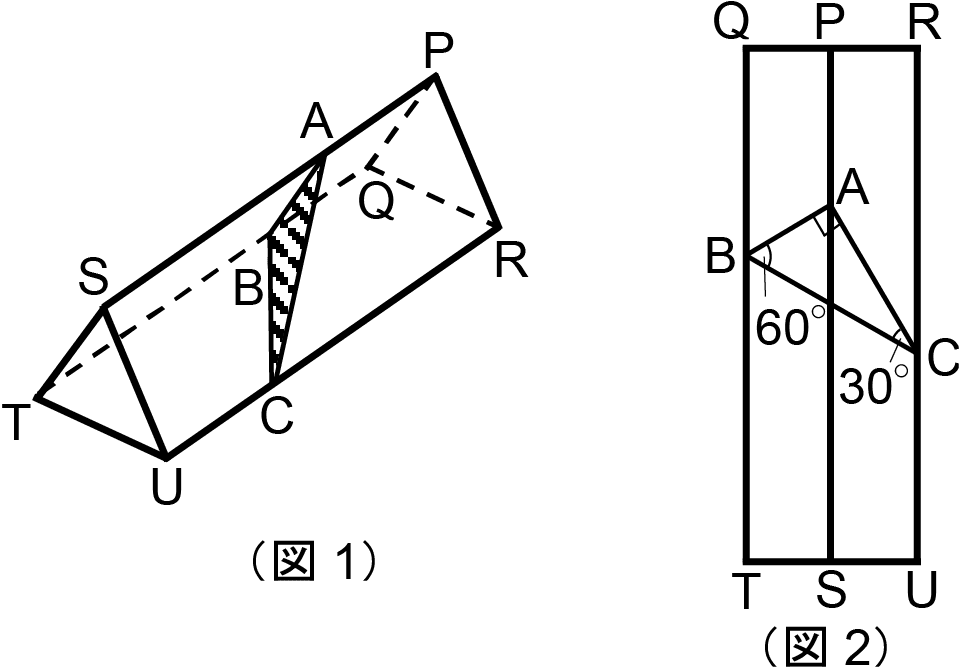
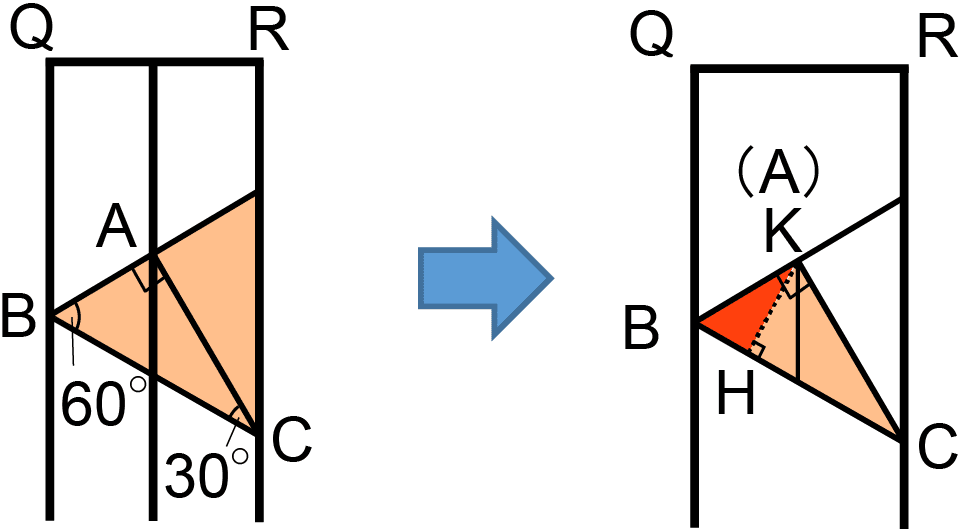
（図１）のように正三角柱を切断したときの切断面（三角形ABC）を真上から見ると（図2）のようになった。この切断面の実際の形を考えようという問題である。
実際の形を決めるには、下の図の、辺BCの長さ、AHの長さ、点Hの位置がわかれば三角形をかくことができる。（ヒカルさんの考察の3段落目）
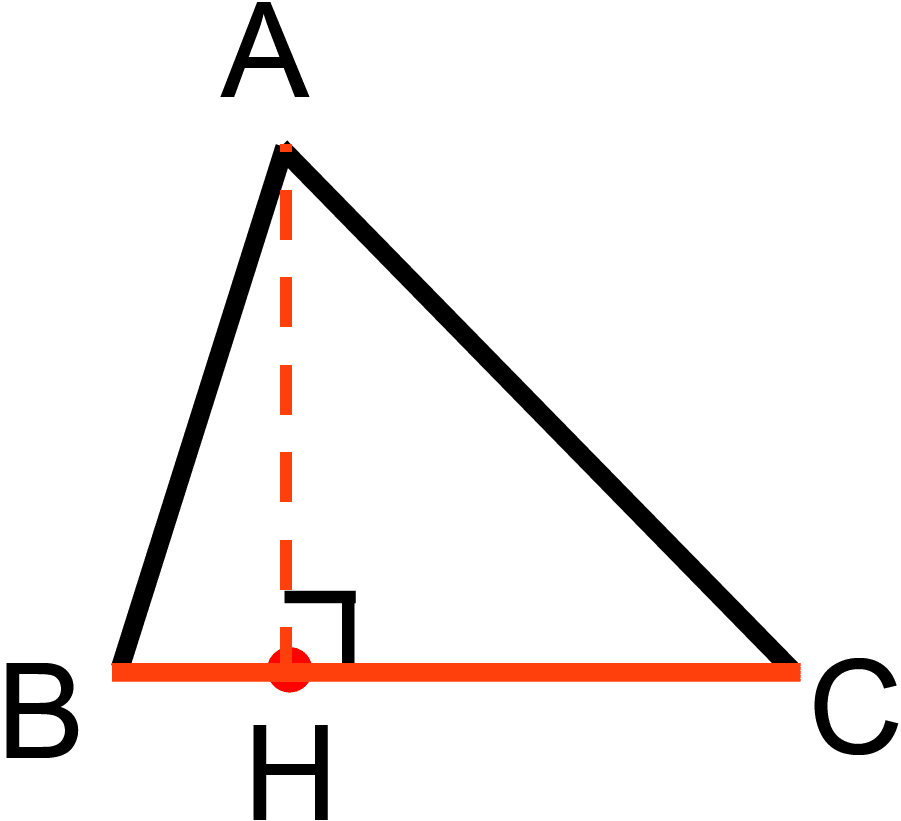
このうち、辺BCの長さは正三角柱の底面の1辺QRを使って表すことができる。真上から見ても辺QR、辺BCの長さは変わらず、三角形ABCを真上から見たときの形は正三角形を半分にした形だからだ。（ヒカルさんの考察の2段落目）
※（2）（図 4）では、すでに辺 QR の長さ、辺 BC の長さが上の条件に合うように解答らん内にえがかれている。
では、AHの長さ、点Hの位置はどのように考えればよいか。ここから、ヒカルさんの考察の4段落目（（ア）の問題）に入っていく。
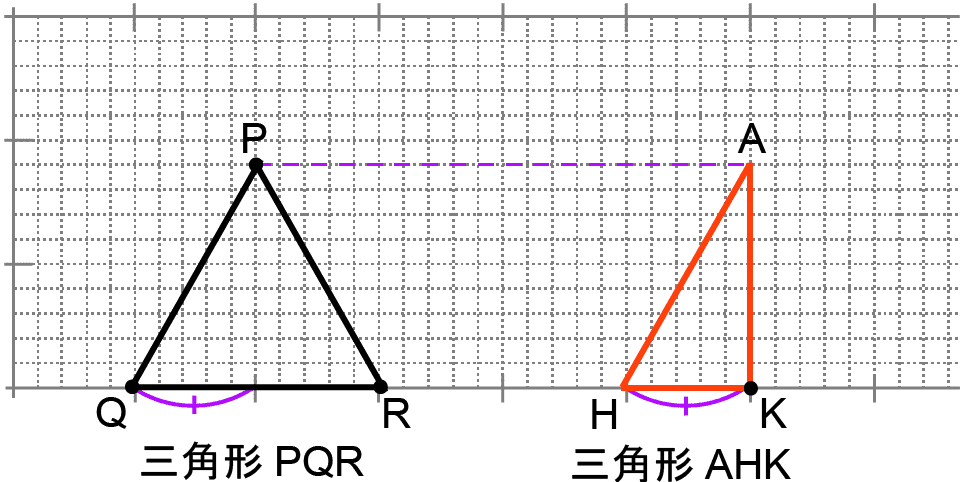
（図2）で真上から見た形を考えているので、点Aの真下、平面QTUR上の点を点Kとする。三角形KBCは三角形ABCを真上から見たときの形だから、三角形KBCは、角Kが90度（ア）、角Bが60度（イ）、角Cが30度（ウ）の直角三角形となる。
三角形KBCは正三角形を半分にした形だから，KBの長さはCBの長さの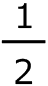倍である。また、ヒカルさんの考察の5段落目より，HKとBCは垂直に交わっているから，三角形HKCと三角形KBCは相似であり、HKの長さはCKの長さの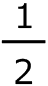倍（エ）である。
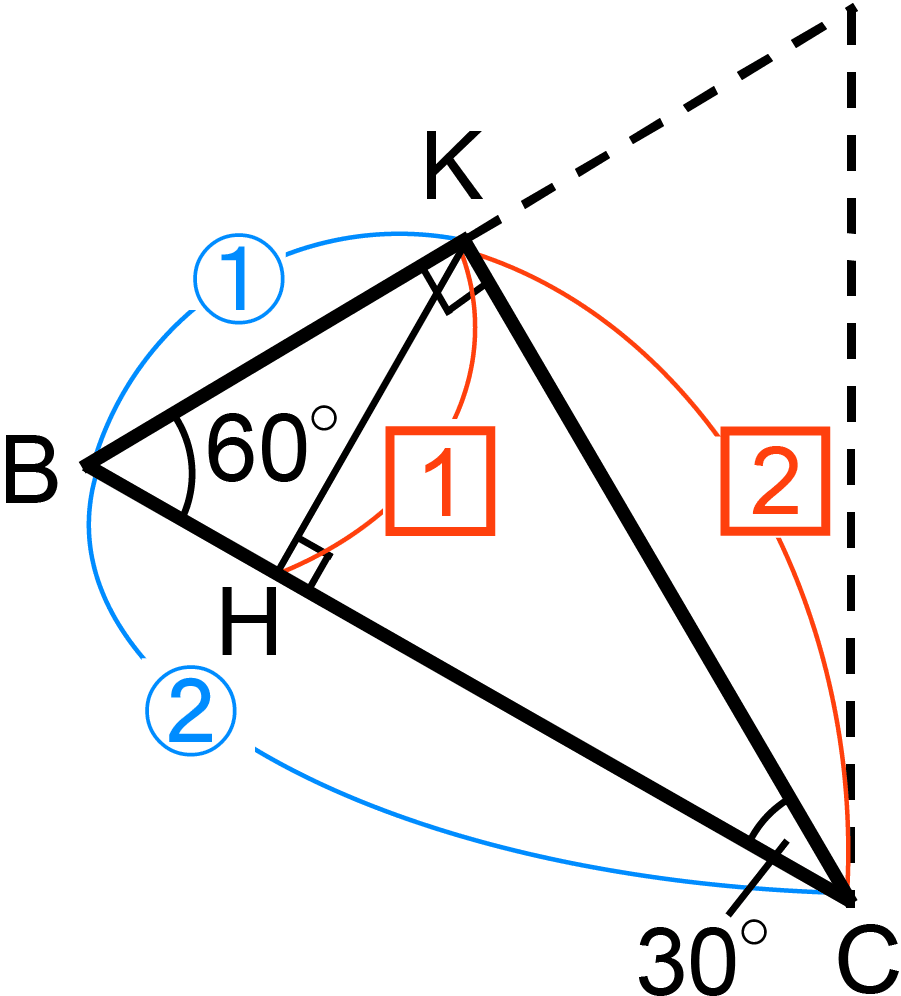
問題文の、HKとBCが垂直に交わることはどうしていえるのかについて補足しておく。点Hはもともと三角形ABCにおいて、辺BCとAHが垂直に交わるように辺BC上にとられた点である。つまり、AHは点Hを通る辺BCに垂直な平面X上にある。そして、この平面Xは、辺BCをふくむ平面、たとえば三角形BKCをふくむ平面QTURとも垂直である。
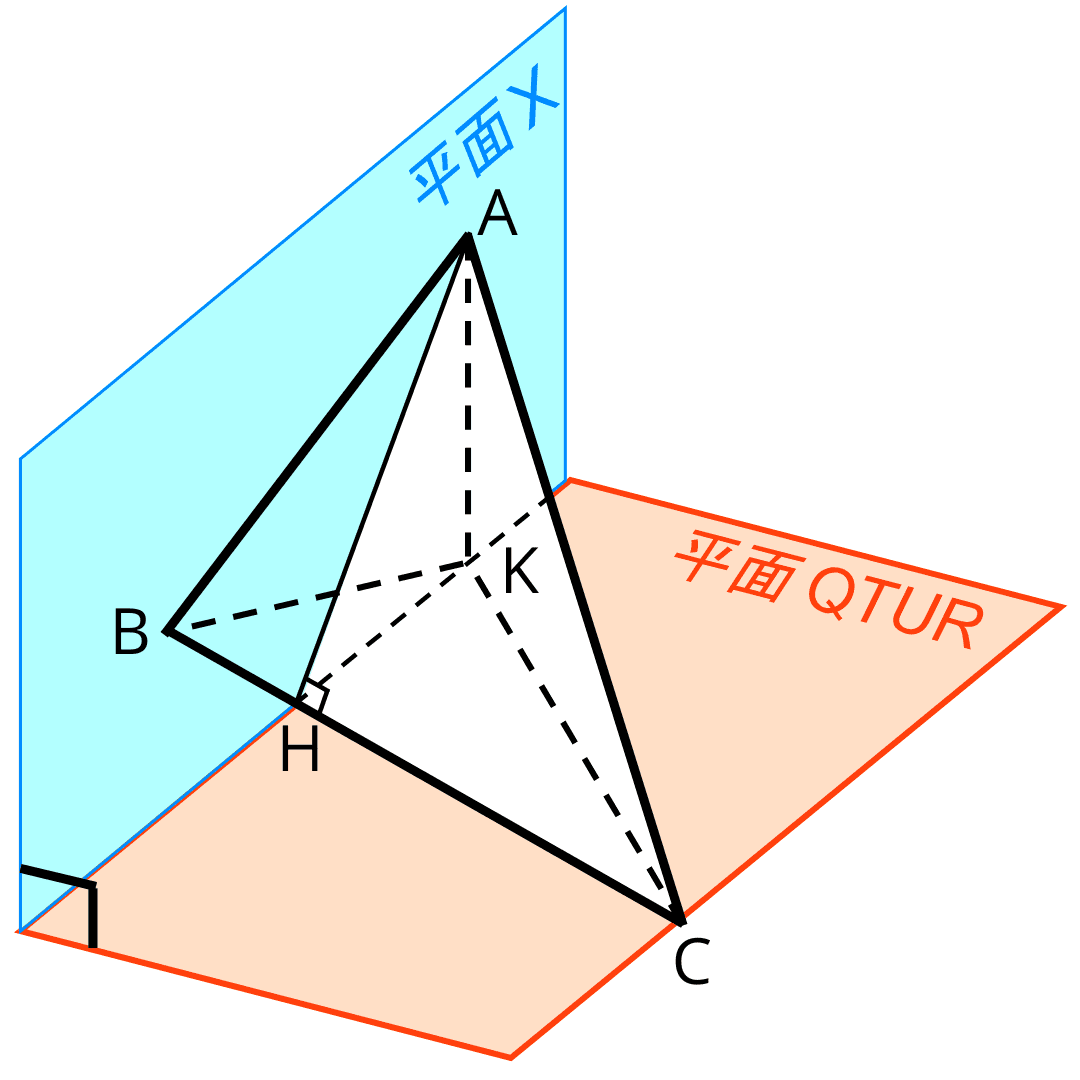
平面QTURと垂直な平面X上にある点Aは、点Aから平面QTURに垂直な線AKを引いたとき、AKも平面X上にある。つまり、点Kも点Hを通る辺BCに垂直な平面X上にあるため、HKは辺BCに垂直とわかる。
さて、KBの長さはCBの長さの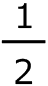倍であり、三角形KBCの角Bは60度だから、辺BCの真ん中の点をMとすると、三角形KBMは正三角形（オ）である。三角形KBHは正三角形KBMを半分にした形だから、BHとHMの長さは等しく、点Mは辺BCの真ん中の点だから、BMとMCの長さは等しい。したがって、BH：HM：MC＝1：1：2であり、HCの長さはHBの長さの、（1＋2）÷1＝3（倍）（カ）である。
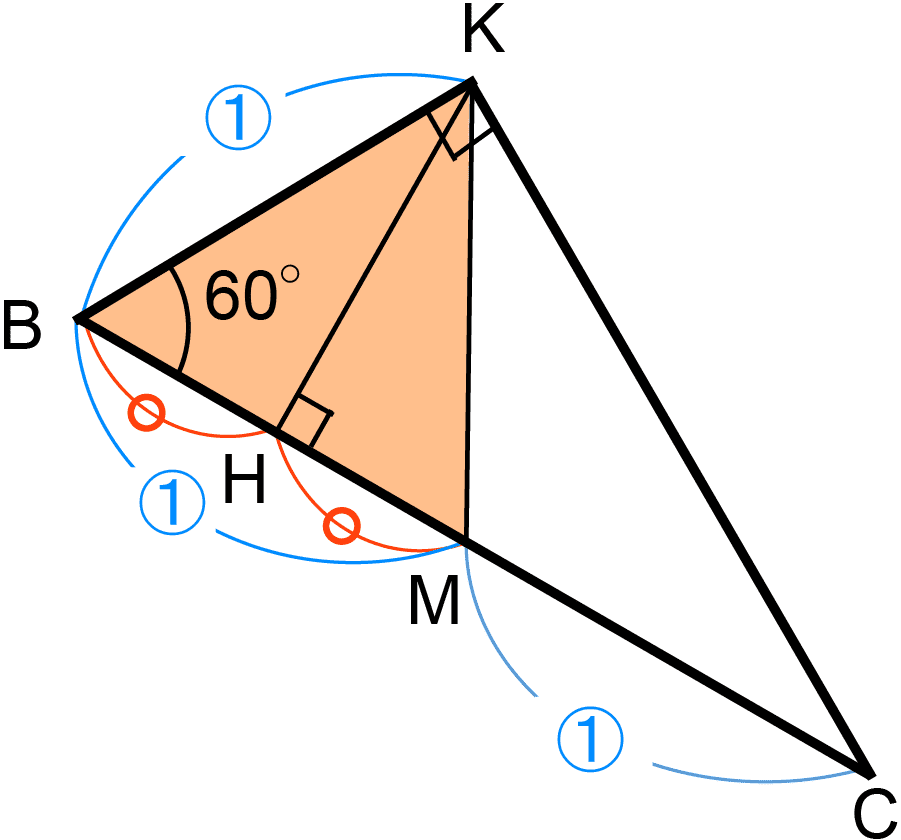
そして、（キ）を考えるにあたり、解説のはじめのほうで触れた（図★）を利用する。（図★）より、QRは辺BCを1辺とする正三角形の高さである。そして、HKは辺BKを1辺とする正三角形の高さである。
BKの長さはBCの長さの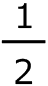倍だから、HKの長さはQRの長さの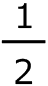倍（キ）である。
（2）解説
（１）にある内容を図示する問題である。
三角形AHKは、ヒカルさんの考察の6段落目より、
・HKの長さはQRの長さの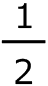倍（キ）
・AKの長さは正三角形PQRの高さに等しい
・角Kは直角（AKが平面QTURと垂直なため）
だから、以下のように作図できる。
ここで、AHの長さをはかりとることができる。
点Hの位置は、「HCの長さはHBの長さの3倍（カ）」だから、辺BCを1：3に分ける点である。
したがって、三角形ABCは以下のように作図できる。
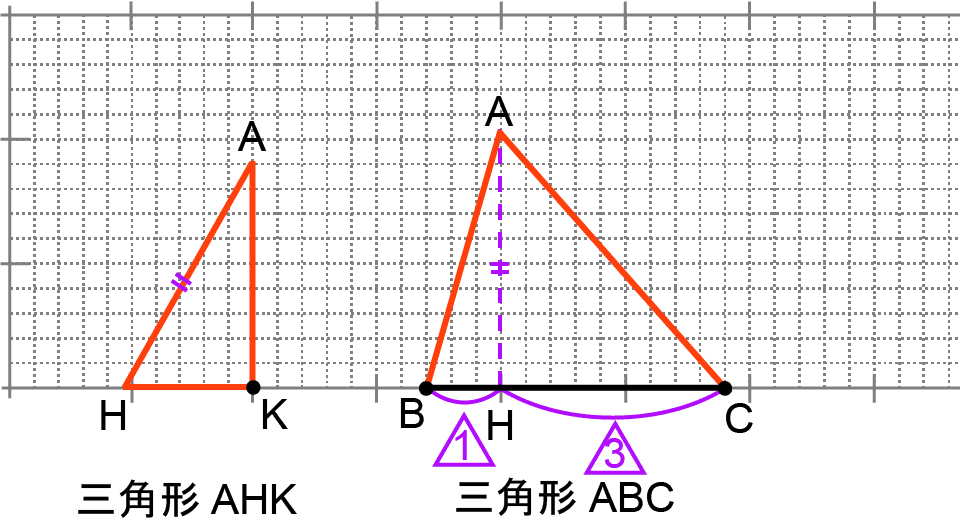
コンパスで作図することもできるが、三角形AHKは、条件から正三角形PQRを半分にした形と合同であるとわかる。
つまり、AHの長さは正三角形PQRの1辺の長さと等しいため、辺QRと同じ長さを方眼からはかりとる方法もある。（点Q，点Rは方眼の格子点よりもややずれているため、AHは10マスよりも少し長くとるとベストだろう。）
【開成対策に！】Ｚ会の専科講座【算数】
短期完成の「Ｚ会中学受験コース 専科」。塾での学習と並行しても負担の少ない教材量で添削指導までついており、通塾の方にもプラスオン教材としておすすめです。
「頻出分野別演習」の他にも、開成中学を想定した予想問題をお届けする専科「志望校別予想演習」、超難問群に取り組む「最難関中学受験プレミアム講座」などもございます。今の学習状況・やりたいことに合わせてご受講ください。
「Ｚ会 筑駒・開成受験応援LINE」のご案内