「お子さまに寄り添った添削」「充実した解説」を日々お届けしている通信教育のZ会が、2023年度筑駒の入試問題「算数」を詳細に分析しました!
入試問題の概観と大問1つを厳選し、Z会ならではの視点で解説をまとめましたので、ぜひお役立てください。
入試概観・解説(筑波大学附属駒場中学校)
筑波大学附属駒場中学校の算数を徹底分析!今年の入試問題の概観と、筑駒中ならではの問題「大問3」の詳細解説を掲載。複数の解法を紹介しますので、解いた人は自分の解法に合わせて、まだ解いていない人は自分に合った解き方をご確認ください。
概観
入試問題全体を通して
非常に筑駒らしい、算数の発想力と計算力の両方がバランスよく要求される問題群であった。
「これはどうやって解けばいいのか?」と解法から悩むような問題は少なく、多少の遠回りを許容するなら丁寧に時間をかければ正解は導き出せる問題がほとんどだった。
しかし、試験時間が40分のため、「丁寧に時間をかけすぎると間に合わない」のは例年通り。解き方は思いつきやすいが「うっかり」ミスを誘発するポイントが多いため、注意して取り組みたい。
大問1
倍数と集合と周期性が合わさった、まさに「ザ・筑駒」という問題。
「◎の倍数と▲の倍数だけが並んだ数列」「◎の倍数と▲の倍数ではないものだけが並んだ数列」という題材は数の性質では頻出である。
◎と▲の公倍数で周期性があることに気づき、各周期の和がどのように増えていくかに迷わず注目したい。
今回の大問の中では完答したい問題なので、(3)は自分が何周期を考えているのか、油断せず確認し、確実に得点したい。
大問2
ルールにしたがって数をあてはめる場合の数の問題。問題の条件に合う各位の数字をひたすら書き出して考えていくのが、遠回りのようでも満点への最適ルートと言える。
(4)で(3)を利用する場合は、「上から2段目の最上位は0としてよい」という(3)との違いにきちんと気づかなければならない。
時間を気にして、なるべく前の問題を利用しようとしすぎると陥りやすいポイントのため、気を引き締めたいところ。
大問3
平面図形。いろいろな考え方、補助線の引き方がある。
角度のヒントがわかりやすいため、自分なりに愚直に補助線を引き、各三角形の長さの比を整えれば、答えは導き出せるだろう。複数の解法を後述するので、ぜひ他にどのような考え方ができたか確認してもらいたい。
自分で図をかきながら取り組んだ場合、辺や角度が他の辺や角と置き換わったようにかいてしまったり,かいたあとに見間違えてしまったりしやすい図となっている。問題の図とは左右対称になることもあるため、「この辺は問題の図の三角形のどの辺にあたるのか」を慎重に確認しながら取り組みたい。
今回に限らず、筑駒の平面図形は「相似」や「対称」に注目する出題が多い。Z会『頻出分野別演習』平面図形難問対策では、辺の比と面積、対称に関して難関校の入試問題もふくめて扱っているので、筑駒の平面図形対策としてぜひ取り組んでみてほしい。
大問4
信号と速さの問題。信号の変わる時間に注目し、丁寧に状態をとらえる必要がある。
横断歩道A・B・Cをそれぞれ通る場合の時間を考え、駅に着く時刻の最速を求めたり、家を出発する時刻の最遅を求めたりするだけの問題だが、その「求めるだけ」の作業を間違えないよう、慎重に取り組む必要がある。
(3)については、お姉さんが横断歩道Cを「渡り始める時刻」という表現から、「お姉さんは信号待ちをするだろうか」という配慮ができたかどうかがポイント。見落とした人も多かったのではないだろうか。細部に注意する必要がある筑駒らしい文章題といえるだろう。
大問3の解説
大問 3(3)は、解くためにいろいろな補助線を引くことができる。今後、平面図形の応用問題に取り組んでいくうえで、身につけておくとよい発想が得られると思うので、ぜひ別解もふくめ確認しておこう。
(1)6:5 (2)30:11 (3)112:195
(1)解説
2つの直角三角形を組み合わせた形なので、問題の図に辺の比をかき入れると、左下の図のようになる。
24=④より、比をそろえると、右下の図のようになる。
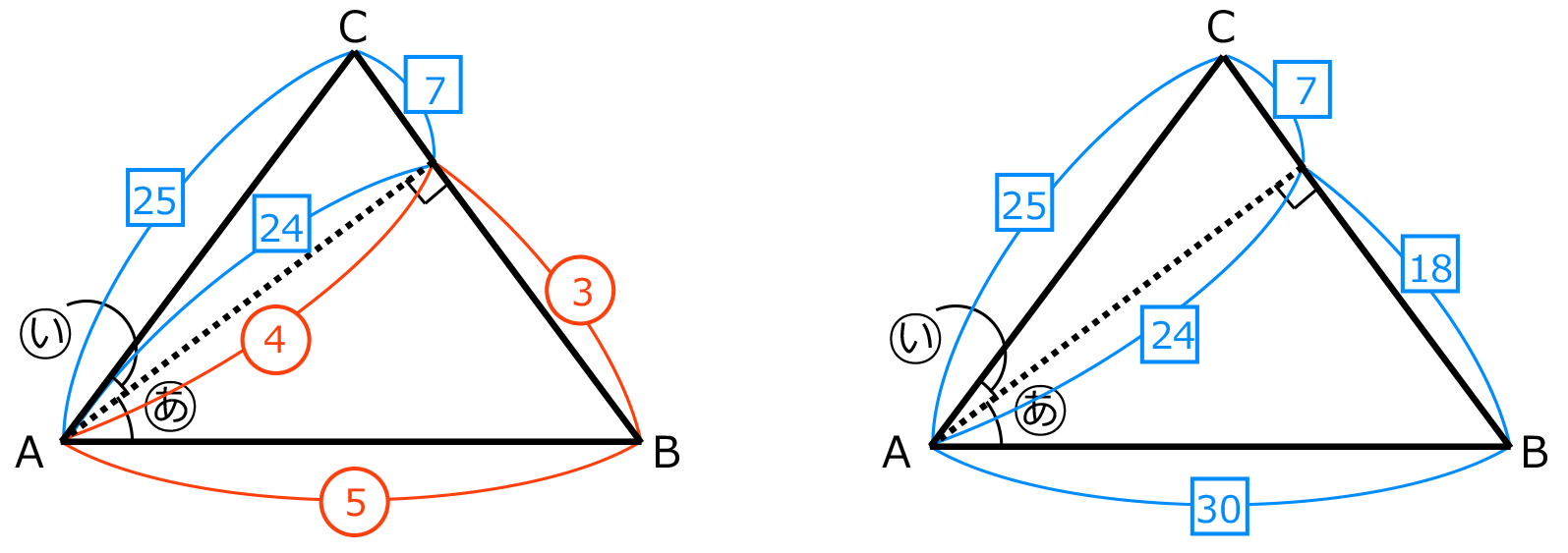
したがって、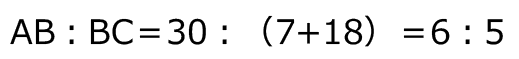
(1)の解説はここまでだが、ここで気づくべきは「三角形 ABC は辺 AC と辺 BC の長さが等しい二等辺三角形」という事実である。三角形 ABC の角 A と角 B の大きさが等しいので、実は最初にあたえられた2つの直角三角形は角度が下のようになっているとわかる。
(角 をもつ直角三角形のもう1つの角は、角
をもつ直角三角形のもう1つの角は、角 をもつ直角三角形の内角の和が、
をもつ直角三角形の内角の和が、 +
+ +
+ +90=180(度)となることから求められる。)
+90=180(度)となることから求められる。)
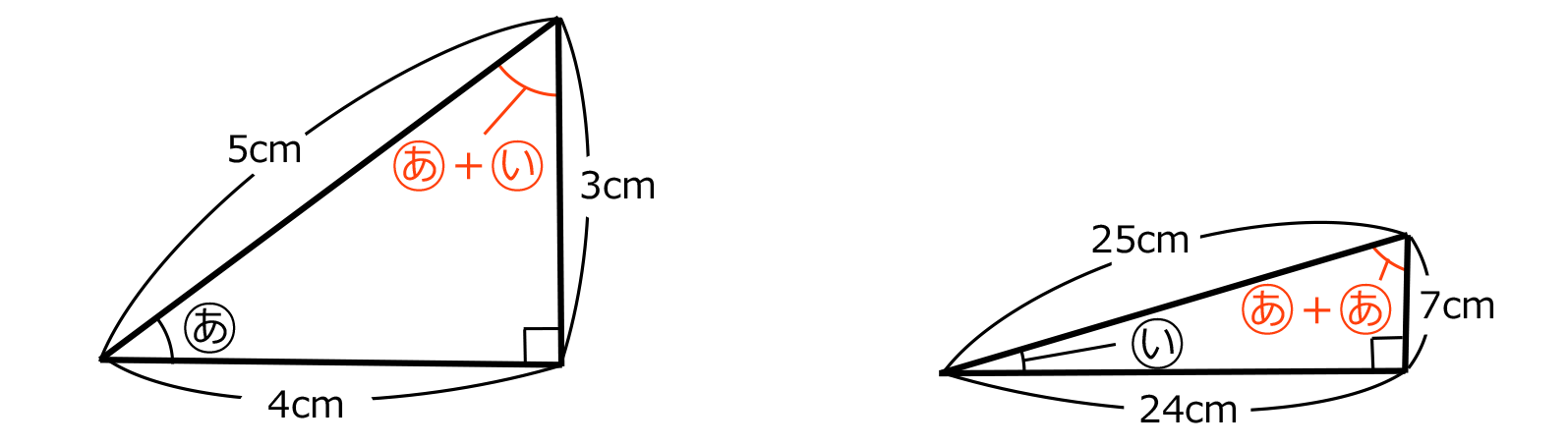
(1)は、(2)と(3)を解くためのヒントに気づいてほしいという出題者からのメッセージだったのだ。
(2)解説
(1)の図を利用すると(1)でそろえた比がそのまま使えて簡単だが、使わなくても解くことはできる。
【解法1;(1)の図を利用する】
(1)の三角形 ABC は二等辺三角形だから、左下の図の点線で折り返せば、右下の図のように(2)の三角形 DEF ができる。
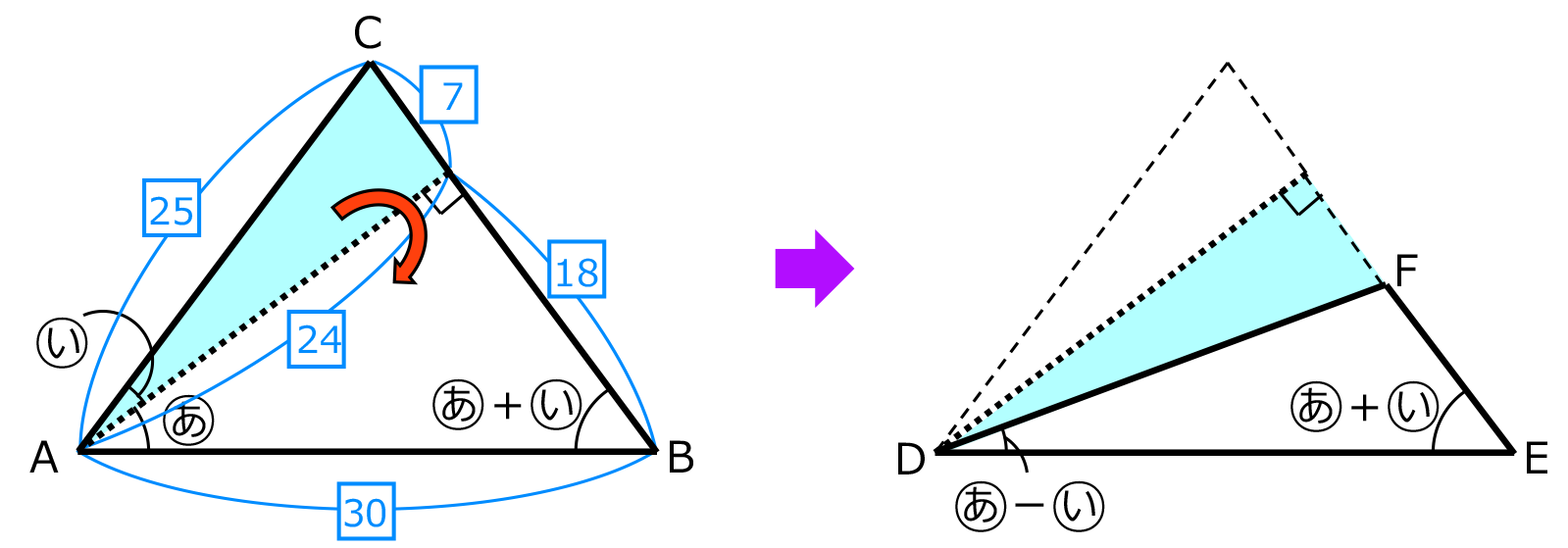
DEは30、EFは18–7=11、DFは25だから、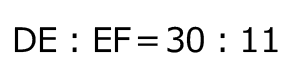
【解法2;2つの直角三角形の図を利用する】
(1)で、角 をもつ直角三角形のもう1つの角の大きさは
をもつ直角三角形のもう1つの角の大きさは +
+ とわかったので、左下の図のように2つの直角三角形を重ねると三角形 DEF になる。
とわかったので、左下の図のように2つの直角三角形を重ねると三角形 DEF になる。
24=④より、比をそろえると、右下の図のようになる。
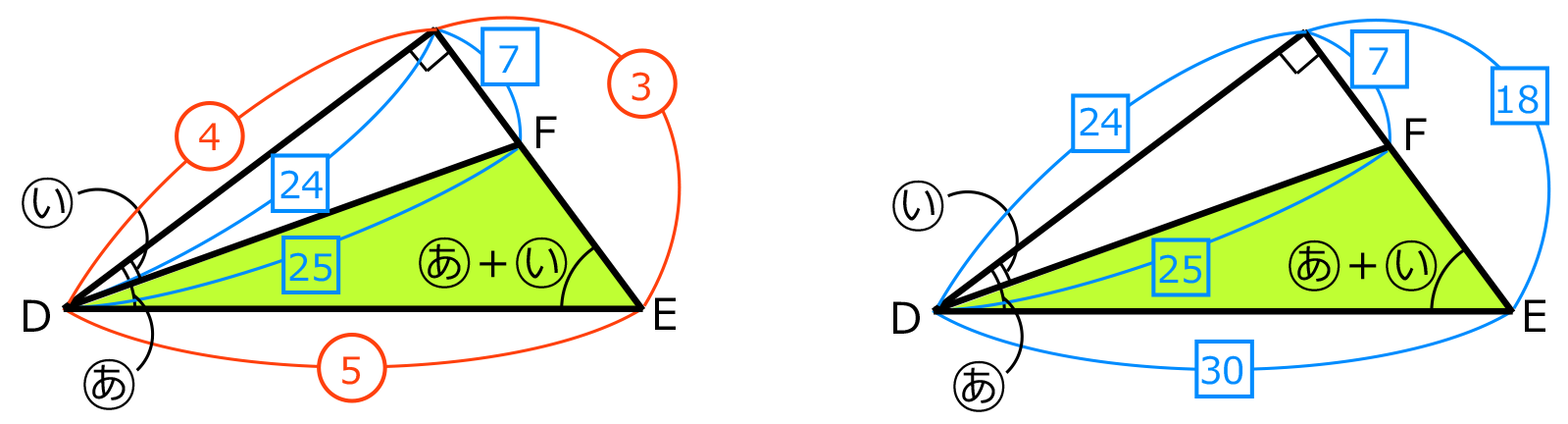
DEは30、EFは18–7=11、DFは25だから、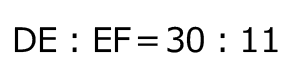
(3)着眼
 +
+ 」をどのように考えるか、が大きな問題となる。
」をどのように考えるか、が大きな問題となる。(1)や(2)の図にも、2つの直角三角形の角度にも、
 +
+ の角度は出てこない。
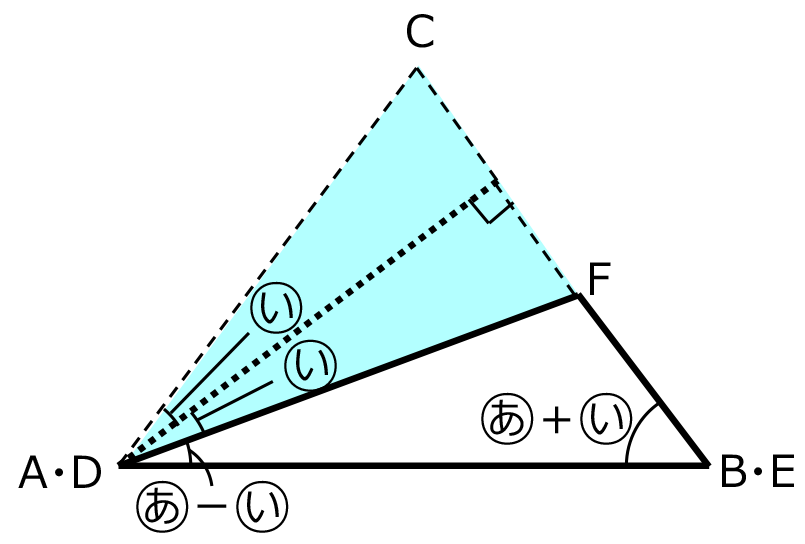
の角度は出てこない。しかし、ここで(2)の【解法1】で出てきた図を思い出そう。
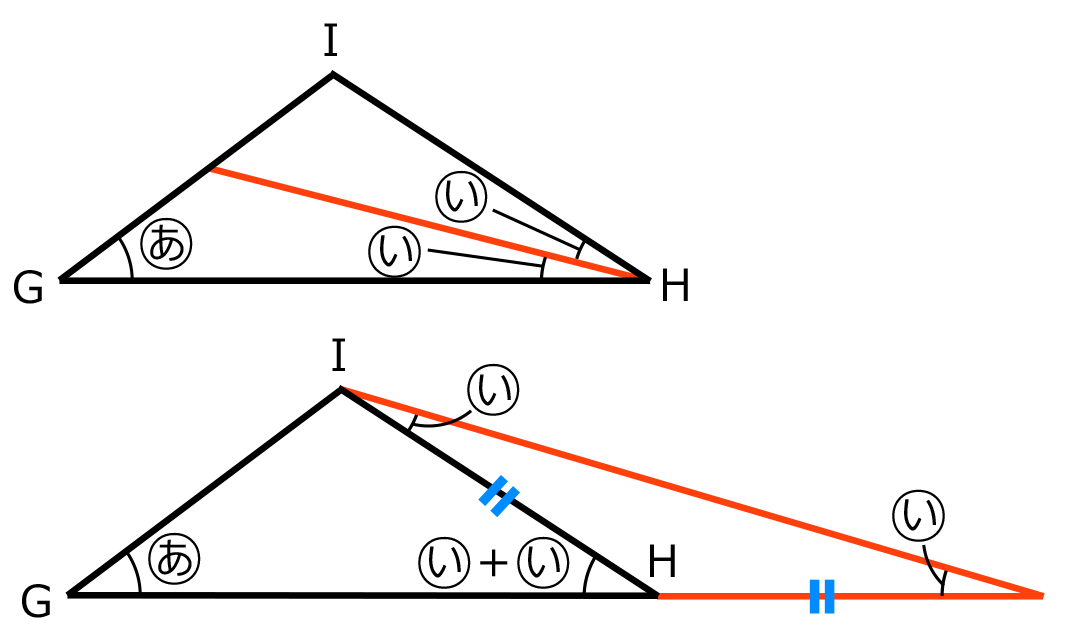
三角形 ABC から三角形 DEF を除いた三角形は
 +
+ の角をもつ。これを利用することで、三角形 GHI をつくることができる。
の角をもつ。これを利用することで、三角形 GHI をつくることができる。
 +
+ は、右のように補助線を引くことで、
は、右のように補助線を引くことで、 の角2つに分けることもできる。
の角2つに分けることもできる。これらをふまえて、(3)では、
・三角形 ABC と三角形 DEF を利用する。
・
 +
+ の角を2等分する。
の角を2等分する。・
 +
+ の角の外角を利用する。
の角の外角を利用する。という3通りの解法を紹介する。
今回紹介するもの以外にも、さまざまな補助線の引き方がある。問題によっては、その中のどれか1つの補助線しか正解を出せない場合もある。平面図形は発想の引き出しを多くもつことで対応力が大きく増すので、Z会『頻出分野別演習』平面図形難問対策も利用して、さまざまな問題に触れておこう。
(3)解法1
【解法1;三角形ABCと三角形DEFを利用する】
このとき、図の★の角の大きさは、
 +
+ となる。
となる。(三角形 DEF の外角ととらえてもよいし、角
 をもつ直角三角形の角として考えることもできる。)
をもつ直角三角形の角として考えることもできる。)この
 +
+ の角を
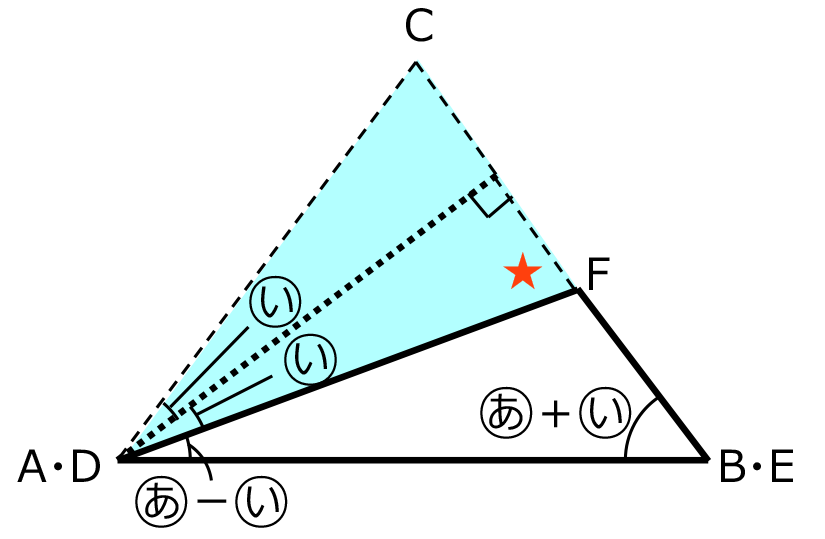
の角を の角2つとしてとらえるため、左下の図のように補助線を引く。すると、色が付いた三角形が三角形 GHI となる。(2)で求めた辺の比をかき入れると右下の図のようになる。
の角2つとしてとらえるため、左下の図のように補助線を引く。すると、色が付いた三角形が三角形 GHI となる。(2)で求めた辺の比をかき入れると右下の図のようになる。
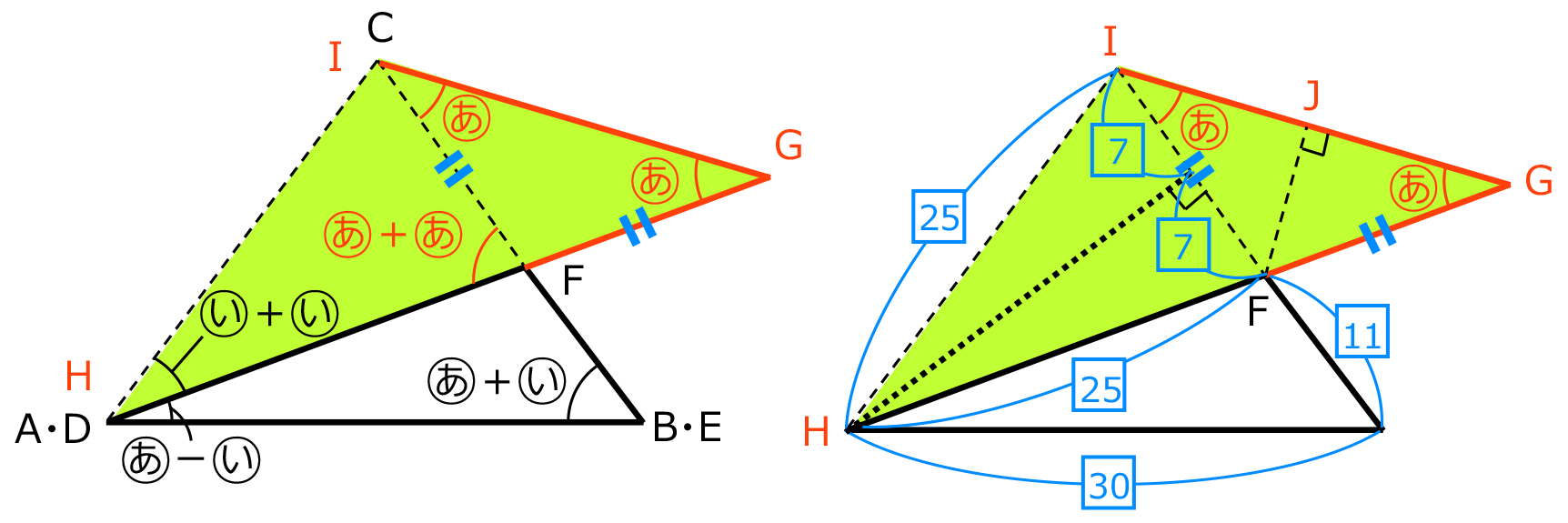
三角形 IFJ は角 をもつ直角三角形だから、IJ の長さは、
をもつ直角三角形だから、IJ の長さは、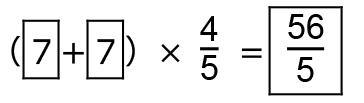
IG の長さは、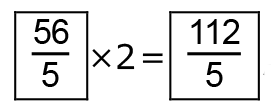 、GH の長さは、25+7+7=39だから、
、GH の長さは、25+7+7=39だから、
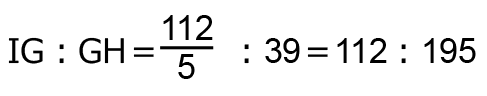
(3)解法2
【解法2; +
+ の角を2等分する】
の角を2等分する】
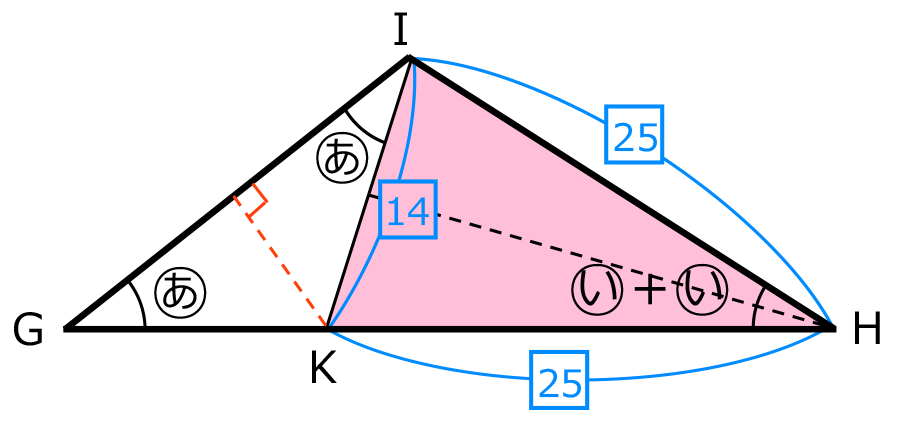
 をもつ直角三角形を2つ組み合わせ、三角形 GHI の中へあてはめると次の図のようになる。このとき、三角形 GKI は角Kの外角の大きさが
をもつ直角三角形を2つ組み合わせ、三角形 GHI の中へあてはめると次の図のようになる。このとき、三角形 GKI は角Kの外角の大きさが +
+ となることから、角Gと角Iの大きさが
となることから、角Gと角Iの大きさが の二等辺三角形になっている。
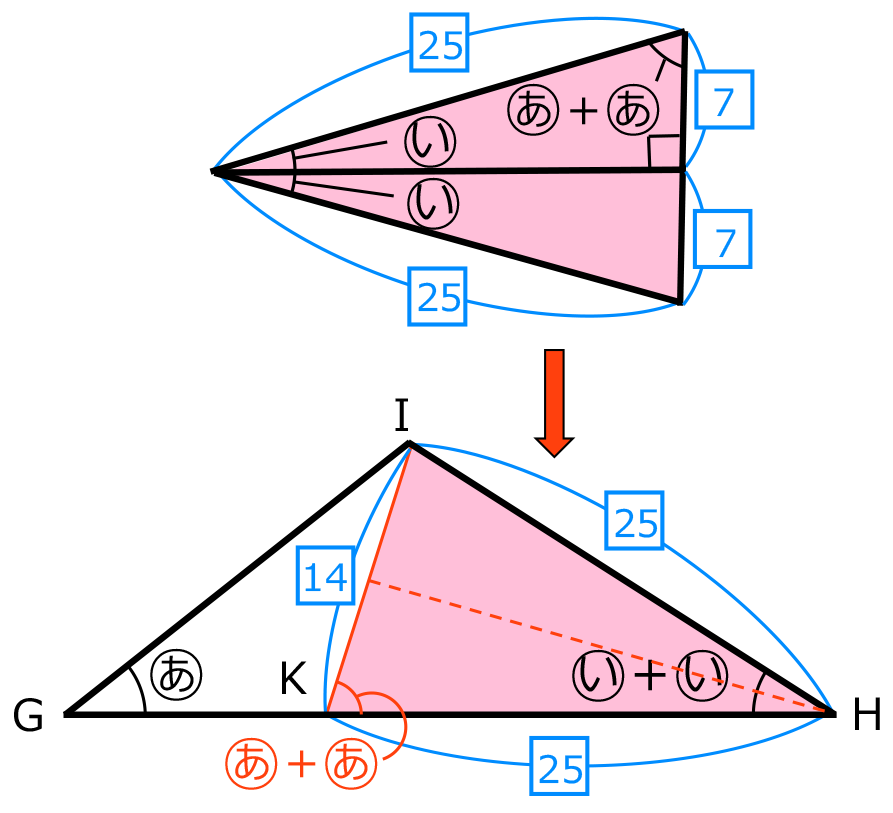
の二等辺三角形になっている。したがって、下の図のように角
 をもつ直角三角形2つに分けて考えると、
をもつ直角三角形2つに分けて考えると、
IGの長さは、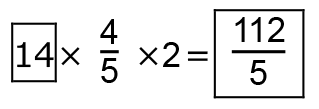
GHの長さは、14+25=39
だから、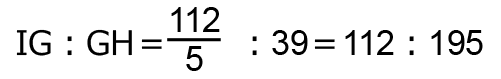
(3)解法3
【解法3; +
+ の角の外角を利用する】
の角の外角を利用する】
 が底角となる二等辺三角形を、三角形 GHI の外側につくる。
が底角となる二等辺三角形を、三角形 GHI の外側につくる。このとき、三角形 GLI は角
 をもつ直角三角形、三角形 ILM は角
をもつ直角三角形、三角形 ILM は角 をもつ直角三角形だから、比をそろえてかきこむと次の図のようになる。
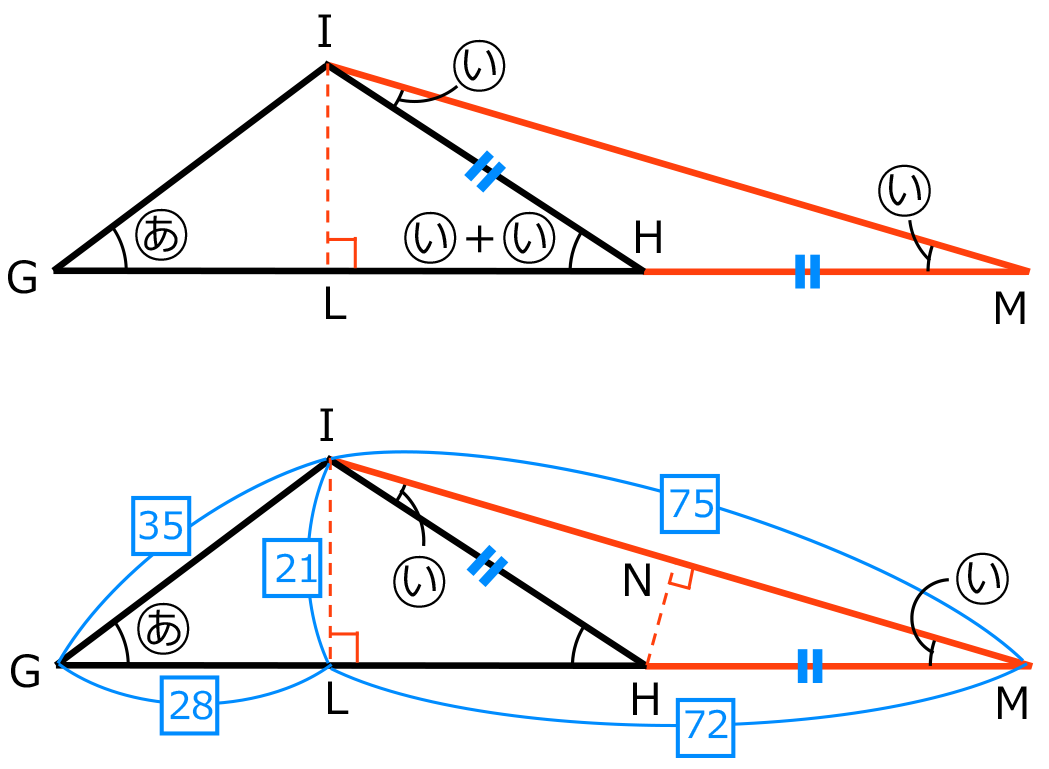
をもつ直角三角形だから、比をそろえてかきこむと次の図のようになる。二等辺三角形 IHM を、角
 をもつ直角三角形2つに分けると、
をもつ直角三角形2つに分けると、NMの長さが、
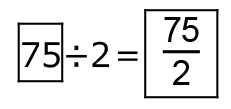
だから、HMの長さが、
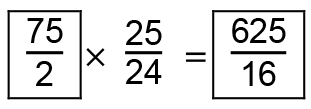
以上より、GHの長さが、
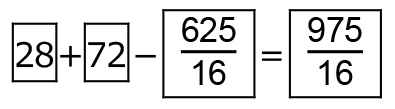
だから、
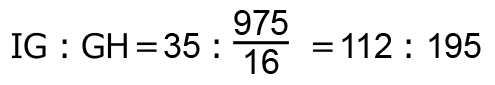
【筑駒対策に!】Z会の専科講座【算数】
3か月完成(毎月1回のお届け)の「Z会中学受験コース 専科」。塾での学習と並行しても負担の少ない教材量で添削指導までついており、通塾の方にもプラスオン教材としておすすめです。
「頻出分野別演習」の他にも、筑駒中学を想定した予想問題をお届けする専科「志望校別予想演習」、超難問群に取り組む「最難関中学受験プレミアム講座」などもございます。今の学習状況・やりたいことに合わせてご受講ください。
「Z会 筑駒・開成受験応援LINE」のご案内
筑駒・開成入試に役立つワンポイントアドバイスをお届けしています。開成の東京問題対策、最難関中学受験プレミアム講座講師からの国語・算数攻略ポイント、過去問の進め方、合格した先輩のZ会活用法など、情報が満載です。ぜひご登録ください!

