「お子さまに寄り添った添削」「充実した解説」を日々お届けしている通信教育のZ会が、2024年度筑駒の入試問題「算数」を詳細に分析しました!
入試問題の概観と大問1つを厳選し、Z会ならではの視点で解説をまとめましたので、ぜひお役立てください。
入試概観・解説(筑波大学附属駒場中学校)
筑波大学附属駒場中学校の算数を徹底分析!今年の入試問題の概観と、筑駒中ならではの問題「大問3」の詳細解説を掲載。
複数の解法を紹介しますので、解いた人は自分の解法に合わせて、まだ解いていない人は自分に合った解き方をご確認ください。
概観
入試問題全体を通して
筑駒らしい、論理的思考力・考察力を非常に求められる、そして算数的興味をとてもくすぐられる問題群だった。
「正確な条件・状況の把握」「適切かつ効率的な場合分け」「短時間での処理」を求めるのは例年の筑駒の算数と同様だが、今年の入試では大問1で「全部で何通りか」答える問題、大問2~4でも「考えられるものをすべて」答える問題が並んだ。
平面図形や立体図形の問題もふくめ、すべての大問で抜け漏れのない場合分けを考えさせるという出題は、「条件にあてはまるすべての場合を把握できているか」という状況把握や適切な場合分けを例年よりもさらに強く問うものであっただろう。
大問1
倍数(あまり)に関する、筑駒頻出の数の問題。
他の大問と比べて筑駒対策の成果が出やすかった問題であり、(3)まですべて正解すべき問題といえるだろう。
大問2
サイコロの面と面を貼り合わせたときに表面に見える目の数の和や、隠れてしまう目の数の和を考察する問題。
「向かい合う面の目の数の和は7」が影響する貼り合わせ方と影響しない貼り合わせ方があるので、立体図形としてはその点に注意する必要があった。
また、「オモテの和」が「ウラの和」でわり切れるかについては、オモテの和(もしくはウラの和)の範囲をふまえたうえで、約数の考察をする必要がある。筑駒は約数・倍数などの数の性質をあつかう問題がとても多いので、大問1に続き大問2も解法を確実に思いついてほしいところ。
大問3
平面図形。正六角形と面積に関する問題で、いくつかの考え方、解き方が考えられる。
(1)~(3)まですべて「考えられるものをすべて答えなさい。」という形式の出題なので、条件に該当するのはどういった状態の場合か、他にあてはまる場合はないのかを意識して取り組む必要がある。
以下に解説を掲載するので、どのような考え方ができたのか、自分が考えたものとは別の解き方はなかったかをぜひ確認してもらいたい。
今回に限らず、筑駒の平面図形は「相似」や「面積比」に注目する出題が多い。Z会『頻出分野別演習』平面図形難問対策では、辺の比と面積に関して難関校の入試問題もふくめて扱っているので、筑駒の平面図形対策としてぜひ取り組んでほしい。
大問4
水の体積の問題で、立体パズルのような思考をする必要がある。
(2)はブロックBのうち1個が確実に水そうの中央に入るため、「その1個が中央のどの位置に置かれているか」「ブロックBの残った1個はどの位置にあるか」と場合分けがしやすい。あてはまる状況が3パターンしかないため、(1)と(2)までは確実に解いておきたい。
(3)については、ブロックBやブロックCの置き方に悩むところだが、ブロックCのほうが置ける場所が限られているため、場合分けの軸として考えやすい。問われているのは水面の高さなので、下から1段目・2段目・3段目と定義したとき、各段に何個のブロックが使われているかを把握すれば最終的には水面の高さが決まることも短時間で解くポイントとなるだろう。
大問3の解説
大問3「正六角形上の点の移動と面積」は、図形的見地・関数的見地の複数の視点から解くことができる問題だった。今後、平面図形の応用問題に取り組んでいくうえで、身につけておくとよい発想が得られると思うので、ぜひ別解もふくめ確認しておこう。
大問3の問題のダウンロードはこちら (517KB)
(1)27秒後、69秒後
(2)6秒後、18秒後、33秒後、63秒後
(3)6秒後、21秒後、30秒後、51秒後
(1)解説
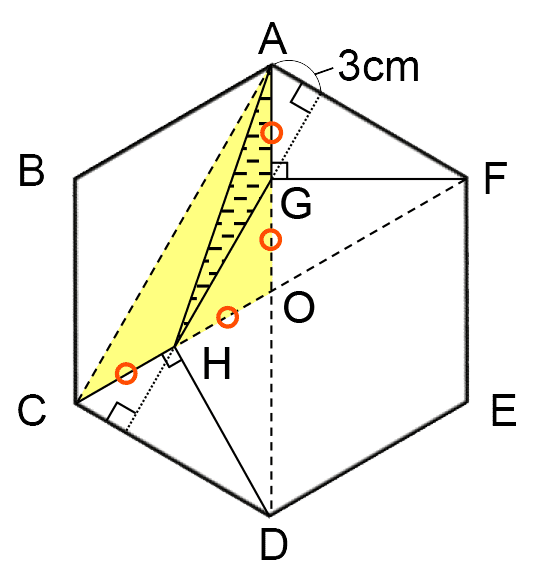
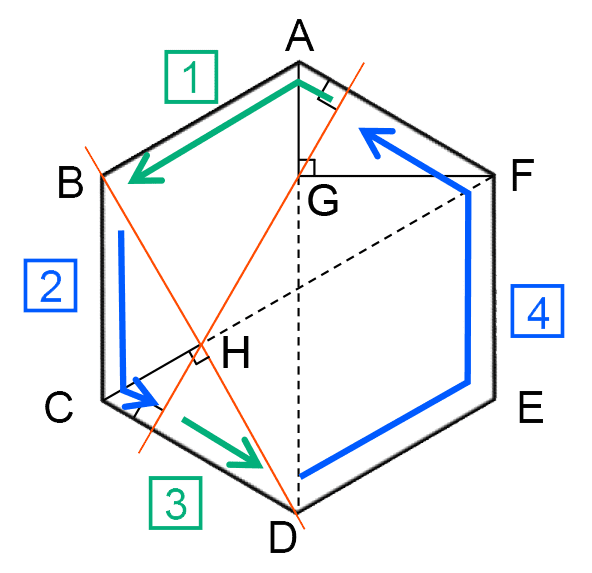
図形PGHが三角形にならないのは、3点P、G、Hが一直線上に並んでいるときである。
つまり、左下の図の2回の位置で起こる。
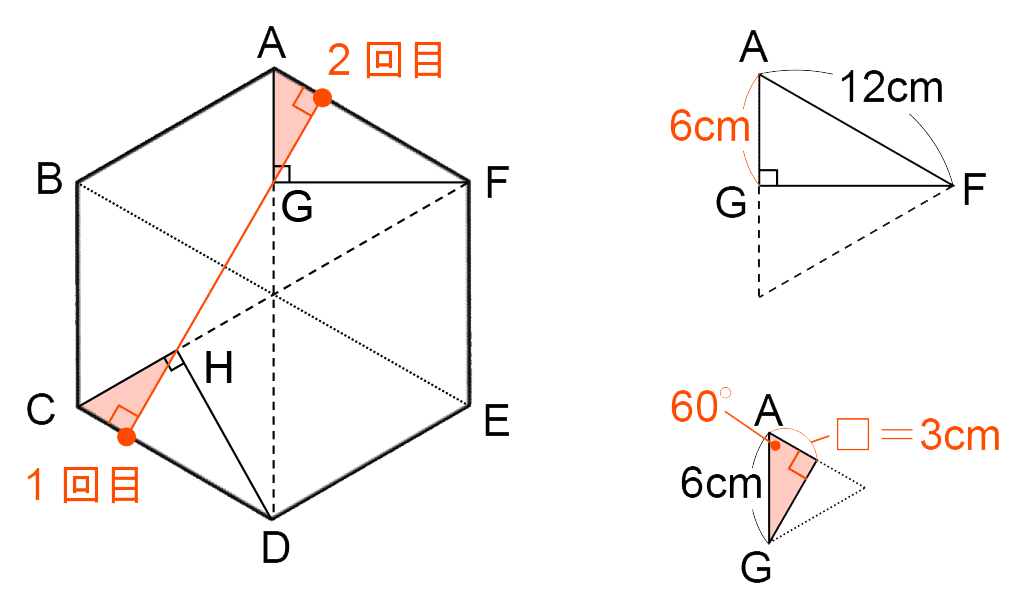
点Gと点HはBEを対称の軸として線対称の位置にあるため、GHはBEと直角に交わる。そしてBEと平行なCD・AFとも、GHは直角に交わる。
三角形AGFは1辺が12cmの正三角形を半分に折った形だから、AGの長さは、12÷2=6(cm)。
同じように、色がついた三角形は1辺が6cmの正三角形を半分に折った形だから、□の長さは、6÷2=3(cm)。
したがって、1回目は、12×2+3=27(cm)より27秒後。
2回目は、1周に72秒(72cm)かかるため、72-3=69(cm)より69秒後。
(2)、(3)概要
(2)、(3)は正六角形の内部にとった三角形の面積に関する問題である。正六角形の内部の面積を考えるときは、補助線を引いて、正六角形全体との面積比で考えていく方法が定石だ。
今回の解説では、(2)で三角形AGFと同じ面積の場合を考えるので、三角形AGFの面積を①、正六角形全体の面積を⑫として考えていく。(「正六角形全体の面積を1とする」など、他の数をおいてもかまわない。)
ここからは、(2)、(3)それぞれについて、
解法1)図形問題として解く
解法2)点の移動と面積の変化に関する問題として解く
という2通りの解法を紹介する。
(2)解法1;図形問題として解く
三角形AGFの面積を①、正六角形全体の面積を⑫としたとき、三角形PGHの面積が①になるときを考える。
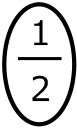 。
。(次の図で三角形AOCの面積は②(正六角形の
 )、
)、点Hは辺COの中点、点Gは辺AOの中点だから、
三角形AGHの面積は、②×
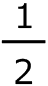 ×
×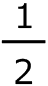 =
=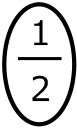 とわかる。)
とわかる。)
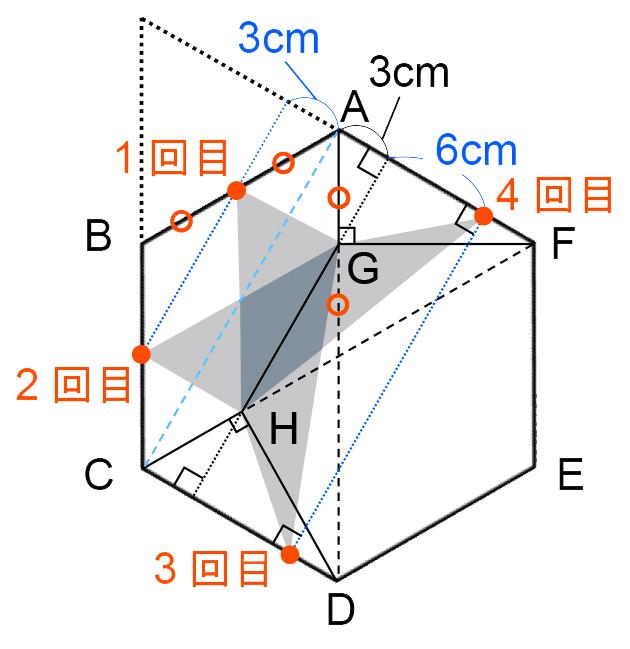
つまり、底辺をGHとしたとき、求める三角形PGHの高さは、三角形AGHの高さの2倍である。
三角形AGHの高さは3cmだから、求める三角形PGHの高さは、3×2=6(cm)。
1回目は、12÷2=6(秒後)
2回目は、12+6=18(秒後)
3回目は、12×2+3+6=33(秒後)
4回目は、72-(3+6)=63(秒後)
(2)解法2;点の移動と面積の変化に関する問題として解く
点Pが正六角形の各頂点上にあるときの、三角形PGHの面積をそれぞれ調べる。
三角形AGHと三角形CGHの面積は、解法1より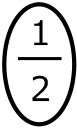 。
。
他の場合については以下のようになる。
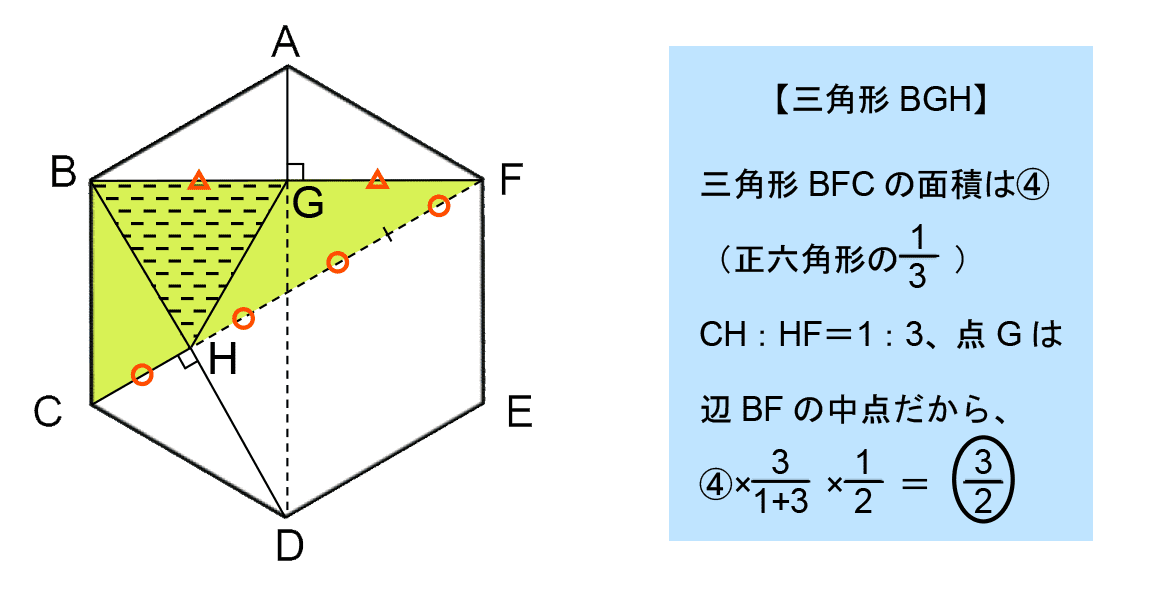
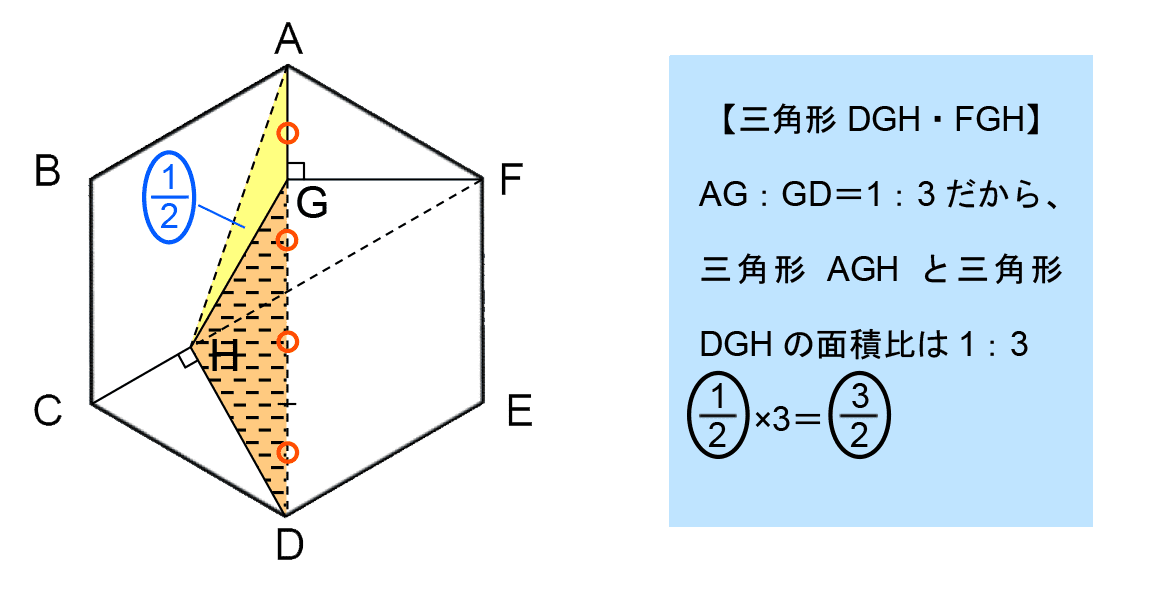
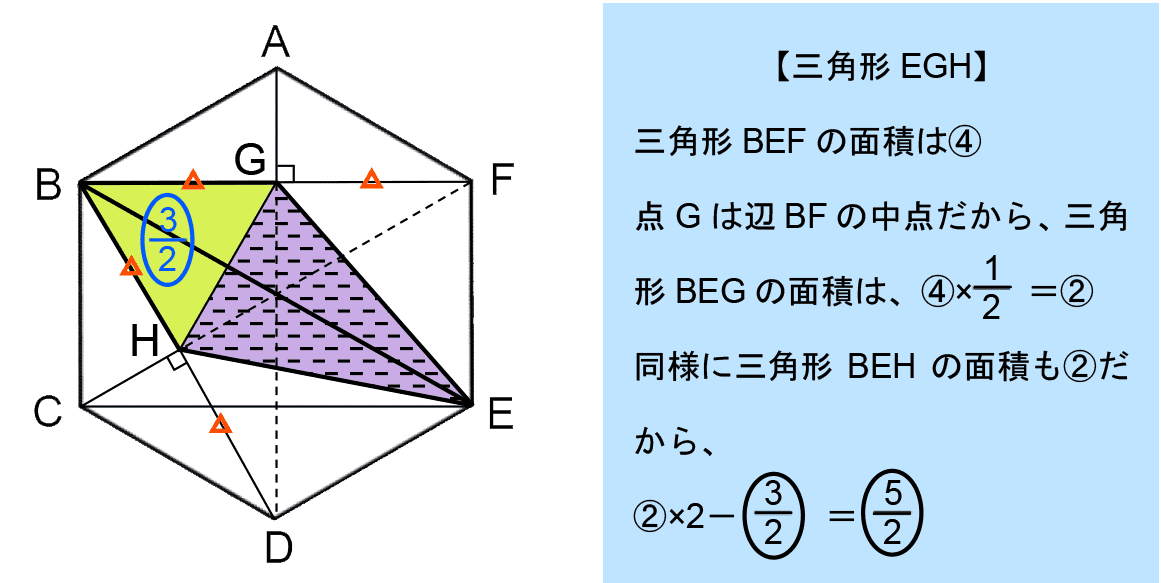
したがって、点Pが動き始めてからの時間と三角形PGHの面積の関係は以下のようにグラフで表すことができる。
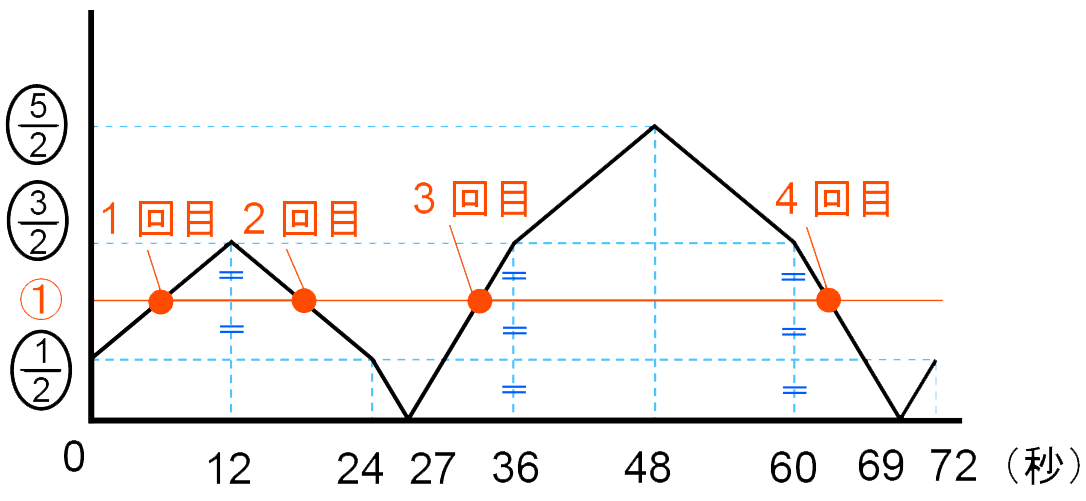
グラフから、面積が①になるのは、
1回目は、12÷2=6(秒後)
2回目は、(24-12)÷2=6、12+6=18(秒後)
3回目は、(36-27)÷3=3、36-3=33(秒後)
4回目は、(69-60)÷3=3、60+3=63(秒後)
(3)解法1;図形問題として解く
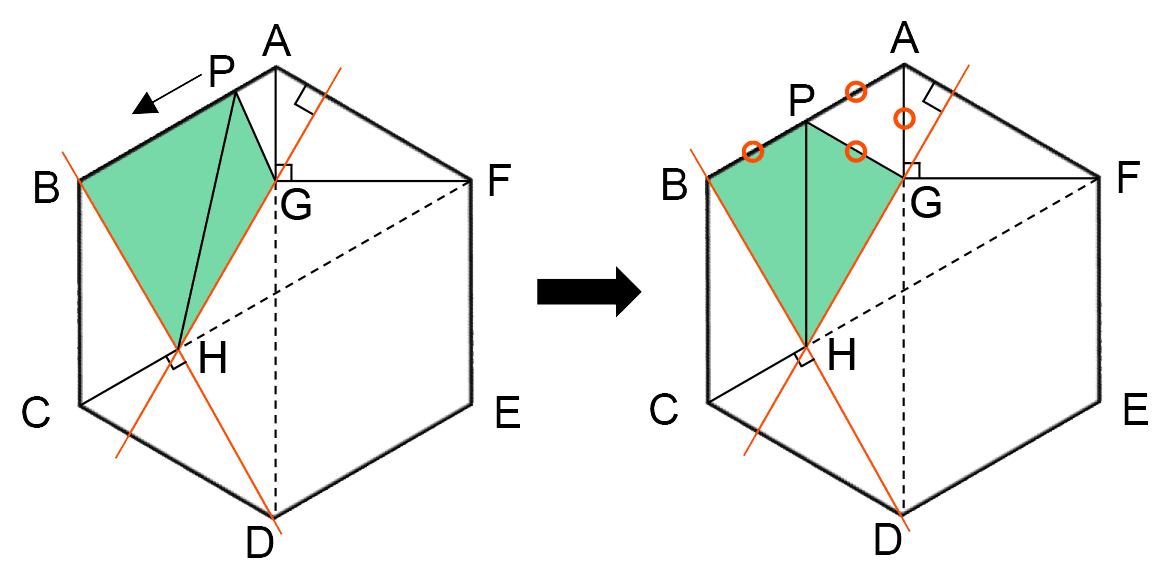
 の区間では、点Pが辺ABの中点にあるとき、三角形PGHと三角形PBHが合同になり、高さと面積が等しくなる。
の区間では、点Pが辺ABの中点にあるとき、三角形PGHと三角形PBHが合同になり、高さと面積が等しくなる。
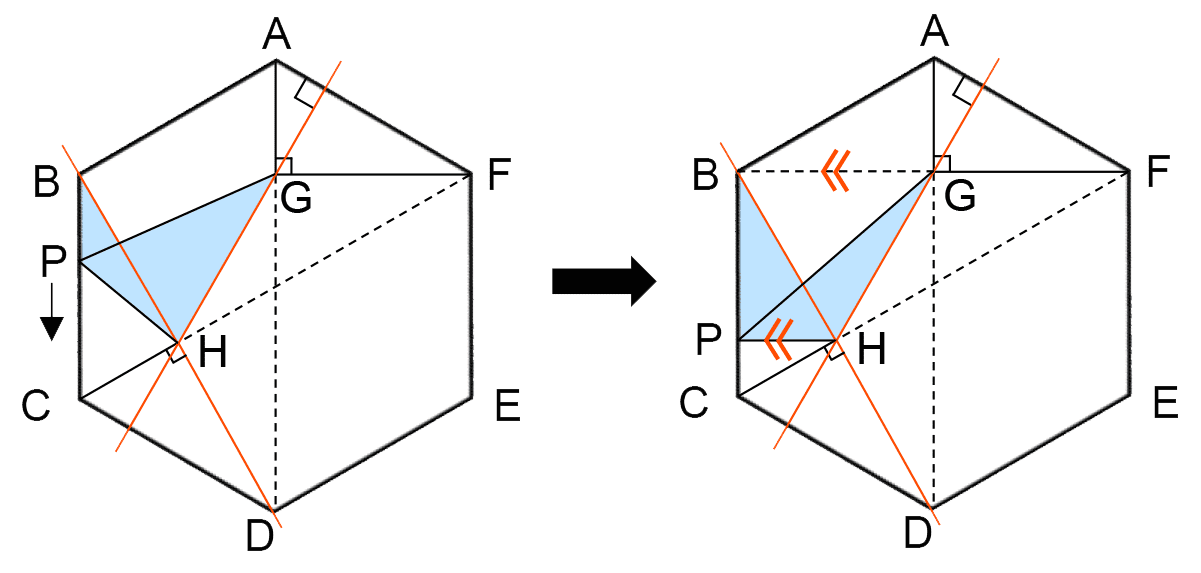
 の区間では、BGとPHが平行になるとき、高さと面積が等しくなる。
の区間では、BGとPHが平行になるとき、高さと面積が等しくなる。
 の区間・
の区間・ の区間もそれぞれ、辺CDの中点にきたときと、BGとPHが平行になるとき、高さと面積が等しくなる。
の区間もそれぞれ、辺CDの中点にきたときと、BGとPHが平行になるとき、高さと面積が等しくなる。
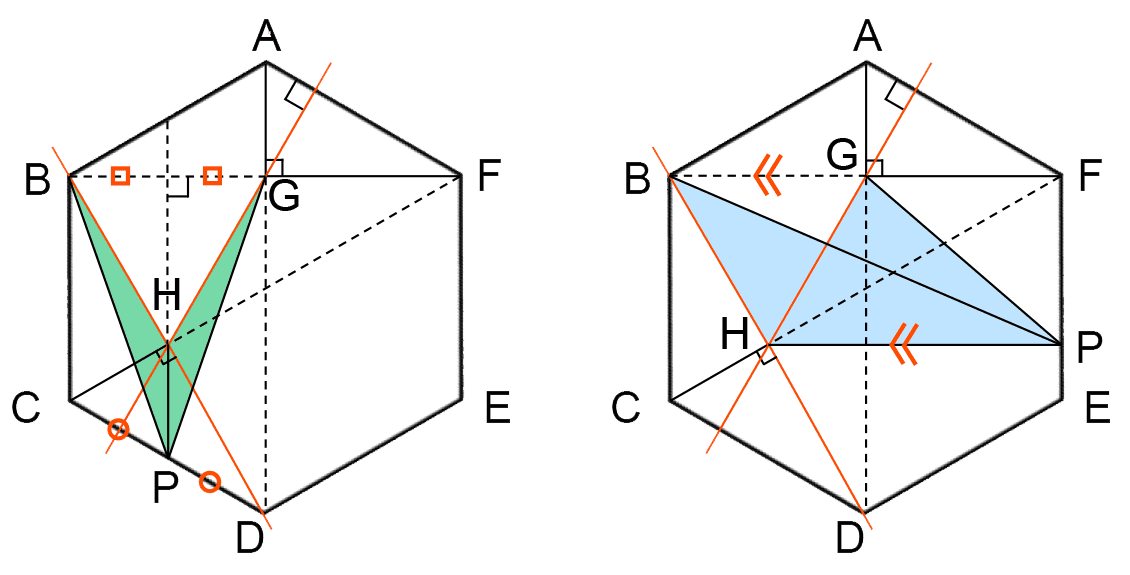
GHとBHは長さが等しいので、三角形PGHの底辺をGH、三角形PBHの底辺をBHとしたとき、高さが等しければ2つの三角形の面積は等しくなる。
ある点からGHとBHに垂直な線を引いたとき、その長さが等しくなるのは、その点が直線BHと直線GHでできた角をちょうど二等分する直線上にあるときである。
したがって、三角形PGHと三角形PBHの面積が等しくなるのは次の図の4回である。
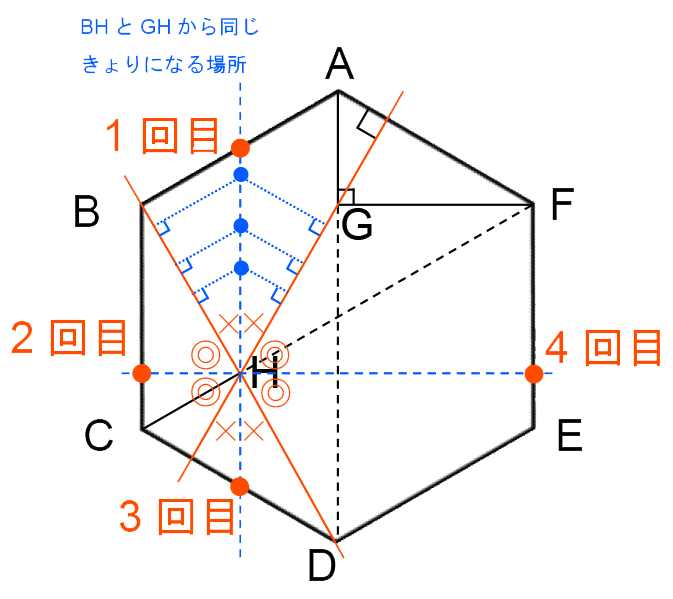
1回目は、12÷2=6(秒後)
2回目は、12×2-3=21(秒後)
3回目は、12×2+6=30(秒後)
4回目は、12×4+3=51(秒後)
(3)解法2;点の移動と面積の変化に関する問題として解く
点Pが正六角形の各頂点上にあるときの、三角形PBHの面積をそれぞれ調べる。
三角形ABHの面積は、三角形ABCの面積と等しく、②。
点Pが点Bや点D上にあるときは三角形にならない。
三角形CBHの面積は①。
三角形EBHの面積は、三角形ABHの面積と等しく、②。
三角形FBHの面積は、正三角形FBDの半分だから、⑫÷2÷2=③。
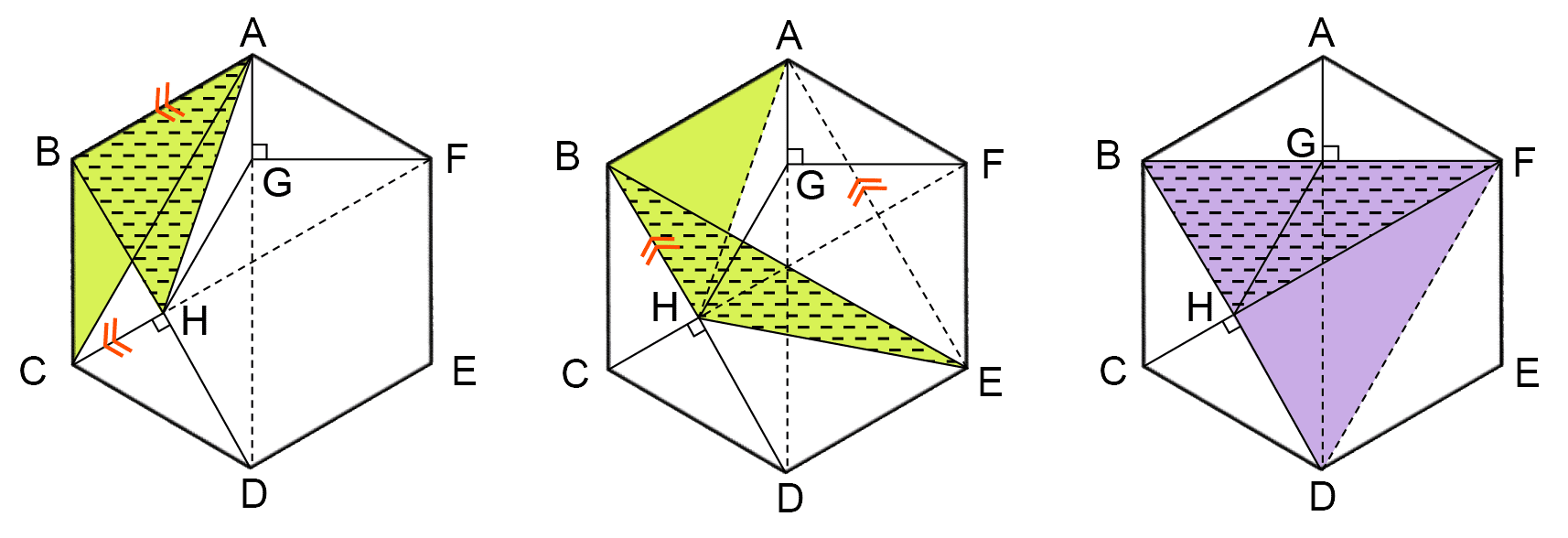
したがって、点Pが動き始めてからの時間と三角形PGH・三角形PBHの面積の関係は以下のようにグラフで表すことができる。
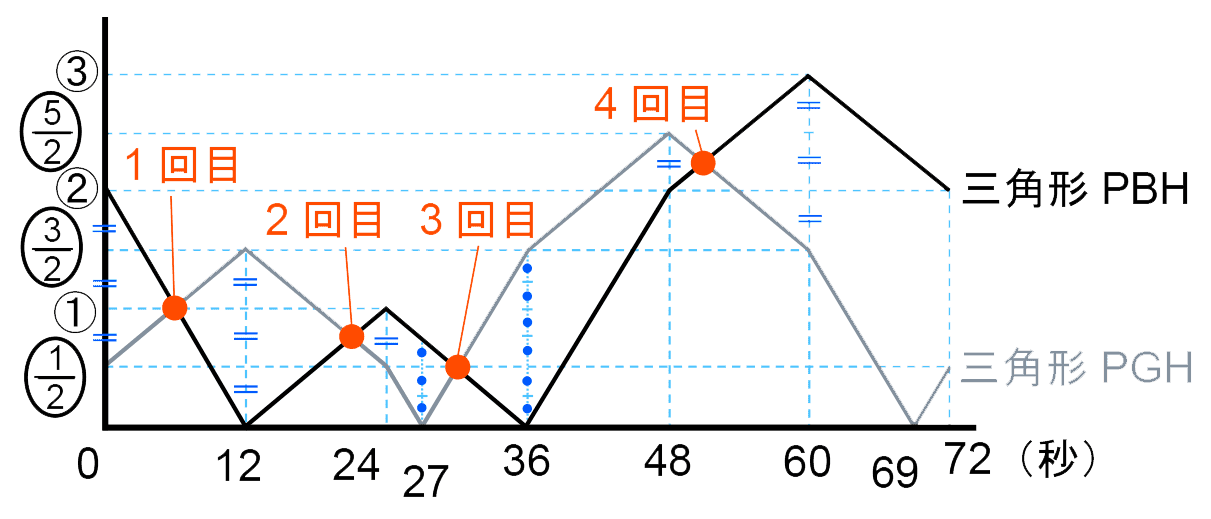
グラフから、2つの三角形の面積が等しくなるのは、
1回目は、12÷2=6(秒後)
2回目は、(24-12)÷4=3、24-3=21(秒後)
3回目は、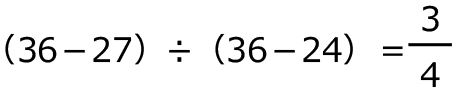 、
、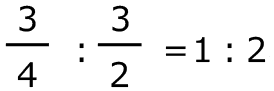 、
、
(36-27)÷3=3、
27+3=30(秒後)
4回目は、(60-48)÷4=3、48+3=51(秒後)
【筑駒対策に!】Z会の専科講座【算数】
3か月完成(毎月1回のお届け)の「Z会中学受験コース 専科」。塾での学習と並行しても負担の少ない教材量で添削指導までついており、通塾の方にもプラスオン教材としておすすめです。
「頻出分野別演習」の他にも、筑駒中学を想定した予想問題をお届けする専科「志望校別予想演習」、超難問群に取り組む「最難関中学受験プレミアム講座」などもございます。今の学習状況・やりたいことに合わせてご受講ください。
「Z会 筑駒・開成受験応援LINE」のご案内

