1月13日、14日と大学入試センター試験が実施されました。数学の試験は2日目に実施されましたが、たとえば『数学Ｉ・数学Ａ』では、長さの大小関係から図形の形状を考えたり、知りたい情報を得るためにはヒストグラムと箱ひげ図のどちらを用いるべきかを判断したりといった、思考力を問う問題が今年も出題されています。

2020年からの新大学入試では、より思考力が重視されるようになるので、このような出題の傾向がより強まるといえるでしょう。

2020年度からセンター試験に代わって実施される「共通テスト」。この導入に向けて、2017年11月に「試行調査（プレテスト）」が行われ、12月にその結果速報として問題の内容やねらいが公表されています。

◎大学入学センターホームページ 試行調査（平成29年11月実施分）の結果速報等について を見る

今回は、この「共通テスト」プレテストの問題を例に、どのような力を身につけるべきなのか、そしてその力を身につけるにはどうすればよいのかについて考えていきましょう。

どのような力を身につけるべき？

「共通テスト」プレテスト『数学Ｉ・数学Ａ』第1問〔1〕では、次の問題が出題されました。

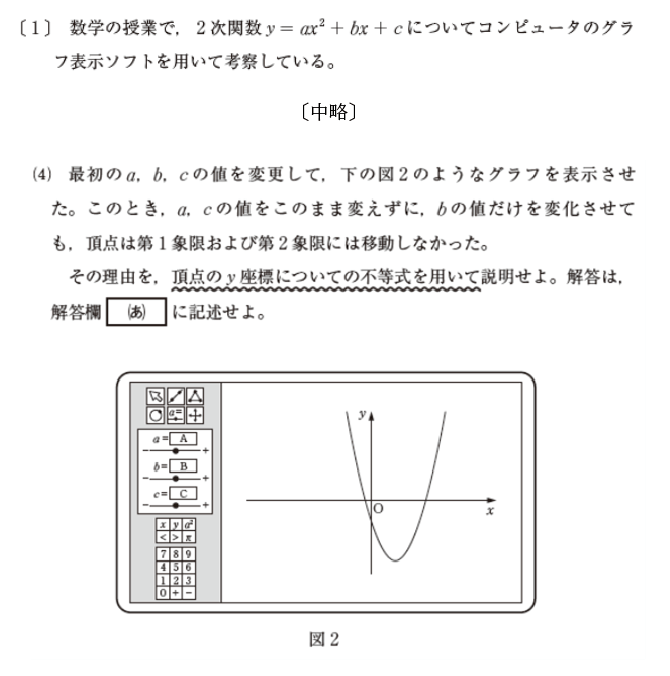
この問題では「2次関数の1次の項の係数の値を変化させたとき、そのグラフはどのように変化するか」が問われており、その出題のねらいは「見いだした事柄の根拠を数学的な表現を用いて説明する力を問う」と公表された資料に記載されています。

つまり、2次関数のグラフに関する知識をきちんと身につけた上で、さまざまなグラフがどうしてそのような形になっているのか、その根拠を考える力が必要なのです。

基礎知識を理解して思考力を身につける学習方法は？

引き続き、2次関数のグラフを例に、話を進めていきます。
2次関数のグラフのかき方は、下の図の上段のように

・平方完成を利用する
・因数分解を利用する

など、たくさんあります。そして、もちろん、1つ1つの基礎知識を、問題演習を通じてしっかりと習得していくことが学習の第一歩となります。

しかし、「問題をたくさん解くことが勉強だ」と思ってしまってはいけません。「与えられた問題について、唯一の答えを導く」ことばかりやっていても、先述のプレテストの問題が解けるようにはならないのです。

思考力を身につけるためには、「与えられた条件のグラフをかく」という演習から、下の図の下段のように「いろいろある2次関数のグラフの形はどのように決まるか」という2次関数のグラフの本質へと、目を向ける先を変えなければなりません。さらに、仕上げとして、応用問題にじっくり取り組み、本質的な理解ができているかをチェックすることが重要です。

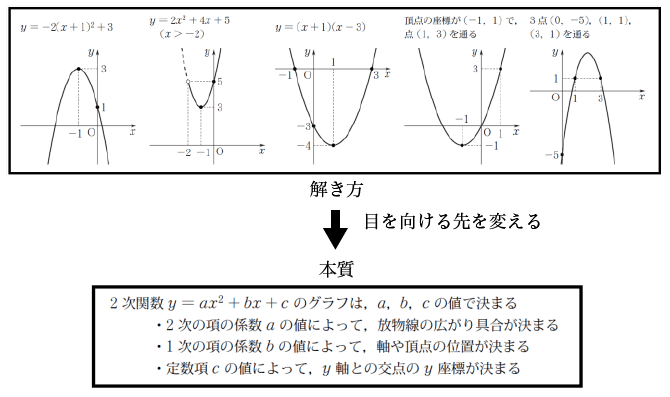
大学入試までまだ時間があるし…と考えてしまいがちですが、こういった「本質的な理解」は時間が一朝一夕にできるものではありません。
自分が納得いくまで調べて深掘りしながら問題を解くことや、考え抜く経験を積むことによって「思考力を問う問題」に立ち向える力がつくのです。

Ｚ会公式おすすめアカウント