こんにちは、子どもたちを見ていると、昔のことを思い出す小田です。わたし自身、それほどまじめな子ども時代を送ってきたわけではないので、子どもたちのいろいろな話(どちらかというと愚痴っぽい話)を聞くと、思わずうなずいてしまうこともよくあります。大人として“こうしてほしい”“こうすべきだ”という理想論はもちろんありますが、それを押し付けるよりも、子どもたちが感じていることを否定せず、そう感じる気持ちそのものは大事にしてあげたいな、と思う今日このごろです。

さて、今回は“分数”についてのお悩みです。前回、小数のお話をしましたが、その続きですね。繰り返しになりますが、「分数・小数はそもそもとても難しい」ということを、忘れてしまわないことがやはり大事です。

それでは早速行ってみましょう。

お悩み4：分数・小数は難しい（分数編）

 

さんすう力UPのポイント

分数の掛け算を理解するために必要なこと

この“お悩み”はとてもすばらしいですね。まさに「新しい世界の入り口には入ったものの、今までと勝手が違ってとまどっている」という様子が見て取れます。

前回もお伝えしたように、「分数・小数を学習する」というのは、「新しい世界に入っていく」ということでもあります。そして、これもくり返しになりますが、「新しい世界に入っていく」ときには、“スムーズに入っていける”ことが必ずしも重要ではありません。むしろ、「最初はとまどいながらもそのなかで新しい世界での過ごし方を探り、自分の力でそのカベを乗り越えていく」という経験のほうが、その先の長い“数学人生”においては重要です。

その意味では、今回の“お悩み”のお子さまも、まさにすばらしい機会を得ている、と言うことができるでしょう。ぜひこういったお子さまには、そのカベを越えていただき、貴重な経験を積んでほしいと思うところです。

さて今回のお悩みですが、確かに言われてみると、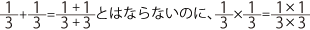となるのは、なんだか不思議な感じがしますよね。まあ、そもそも「足し算・引き算」と「掛け算・割り算」は別の演算なので、同じ計算方法になる必要はまったくなく、むしろ違う計算方法であたりまえ、と言ってしまえばそれまでなのですが。ただ、逆に言えば、別物であるからこそ「足し算・引き算」の延長線上で「掛け算・割り算」を理解するのは難しく、それぞれ個別に理解していかなければいけない、ということでもありますね。「足し算・引き算」の感覚が「掛け算・割り算」では通用しない、という感想は、とてもいいところをついています。

分数の掛け算を理解していくためには、「分数とは何か」ということだけでなく、「掛け算とは何か」ということについての理解ももっと深めていく必要があるでしょう。

たとえば今回の“お悩み”の「1/4のピザを2つ掛け合わせると、どうして小さくなるの？」という部分、「1/4のピザを2つ掛け合わせる」というのは確かに意味不明ですが、よくよく考えると、これは分数だからわからない、というわけではありません。分数ではなく整数にして「2個のピザと3個のピザを掛け合わせる」と考えても、やはり意味不明ではないでしょうか。

掛け算に限った話ではありませんが、“計算”にはそれを適用できる場面とそうでない場面があります。「ピザの個数×ピザの個数」という計算は、整数・分数関係なく、一般的にはあまりやらない計算です。分数の掛け算を理解するためには、また別のシチュエーションを考える必要があるでしょう。

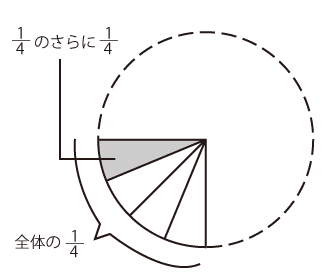
たとえば、「サラミが2枚ずつ載ったピザが3枚ある」なら、サラミの数は全部で「2×3＝6」となります。同様に考えて、「トマトが(1枚あたり）1/4個ずつ載ったピザの1/4切れ」には、トマトが「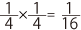」個分載っている、と計算することはできるでしょう。そういうふうに捉えると、「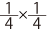」という計算は「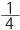をさらに4つにわけたうちの1つ分」と考えることができるので、「4×4＝16個に分けたうちの1つ分になる（分母が変わる）」ことも「答えが元の数より小さくなっている」ことも、納得はいくのではないでしょうか。

どういった場面でその計算が適用できるか（逆に、できないのか）を考えることも、それぞれの計算に対する「理解」の一つなのです。

帯分数の計算を理解するために必要なこと

掛け算以前に、足し算・引き算も、なかなか難しいですよね。

それこそ、 じゃないのか、と思う感覚は納得できますし、そこをクリアしたとしても、今回の“お悩み”のような「帯分数の計算」になってくると、また少しハードルがあがります。

この“お悩み”のように、「帯分数の引き算」で繰り下げることができない、というのは、根本的な原因として“整数と分数の変換”のイメージがまだ深まっていない、というところがあるでしょう。

「1」という数を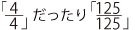だったりという、「分数」で表現する、というところは、慣れるまではなかなか難しいのです。前回もお伝えしたように、そもそも「1つの数をいろいろな表記で表現する」ことを受け入れていくのは、新しい世界に入ったばかりの子にとっては、そんなに簡単なことではありません。しかも、「1」という“最も基本的な数”を「別の表現で表す」というのは、“数”に対する自分の理解を根本から作り直す必要もあり、抵抗感が強くなるのも仕方ないでしょう。「“1”は“1”じゃないの？」というのは、ごくごく自然な感覚です。ただ、そのあたりは結局のところ、時間をかけてじっくりと、納得がいくまで“分数”の世界に向き合っていくしかありません。

帯分数の引き算をするときは、まずは絵をかいて考えるのがいいでしょう。

たとえば、 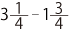であれば、以下のようにかいてみます。
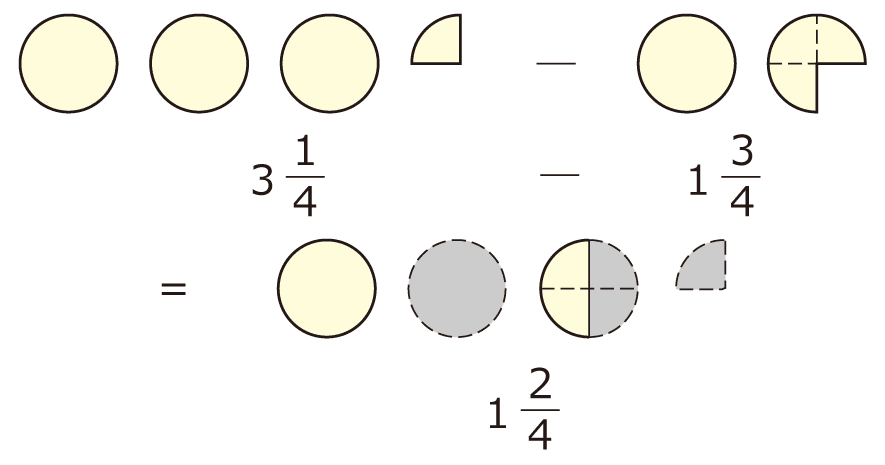“繰り下がる”部分を4分割して「」にし、「引く数」に対応する部分（答えのグレーのところ）を消していくのです。こうして作業をすれば、ひとまずは答えを出すことができますね。まずは実際にこうやってかいてみて、「自分の手で答えを出す」ことから始めましょう。もちろん、絵をかいていきやすいように、整数部分や分母の数が小さい数のものを扱う、という配慮は必要です（整数部分が大きかったり、分母が大きかったりすると、絵をかく作業自体の負担が大きくなるので）。一見、面倒なようにも見えますが、「“帯分数の繰り下がり”というのは、つまりこういうことなんだろう」と、自分のなかで納得がいくまで、何度もこの作業を繰り返し、じっくりと向き合うことが、「帯分数の繰り下がり」を理解していくための実はいちばんの近道です。

「約分ができない」とはどういうことか

なお、「約分を忘れてバツになる」というのは、実はまったく別の話です。「約分を忘れる」というのは「約分できるのに約分せずに済ませてしまう」ということだと思いますが、その原因には大きく分けて2つのパターンがあります。1つは「約分してもいい（分母と分子が同じ数で割れるなら割ってもいい）ことがわかっていない」パターン、もう1つは「実際に計算したとき、約分ができるのに見逃してしまう」パターンです。

前者の場合は、やはり前提として「1つの数を表すのに複数の表現がある」ということを受け入れられるようにならないといけませんし、そのうえで、前者の場合は「分数」についての理解を深めること（約分しても大きさが変わらないことを納得すること）が大事です。こちらも、繰り返し図を書いて、納得していくしかありません。

後者の場合、必要になるのは「分数」への理解でなく「整数」への理解です。約分を“忘れる”と表現されることが多いですが、実際には忘れているのではなく“気づいていない”ことのほうが多いでしょう。分母と分子で共通して割り切れる数のことを分母と分子の「公約数」と言いますが、数を見ただけでこの「公約数」を見抜く、というのは、これもなかなか難しいです。本来なら、「整数」の分野をきちんと学習し、それなりにトレーニングを積んでいって、ようやくこういった「公約数」を見抜く力が養われていくものです。しかし、現在の学校のカリキュラムでは、あまりしっかりとはこの「整数」の分野を扱いません。ほぼ最低限の説明だけで終わってしまうため、もともと数に興味があり、センスをみがいてきた子たち以外には、実際に「どの数で約分できるか」を瞬時に判断するのは、分数の学習以外のところでとても高いハードルになっています。そういう意味では、“分数”のテストにおいては、「約分を忘れた」だけであれば、×にする必要はないのになとは個人的には思っています。とはいえ、学校の先生の指導の方針もあるかと思いますので、各ご家庭におかれましては、余裕があれば「整数（とくに約数・倍数）」の学習を別途進める、もしくは、そういった余裕がなければ「（今の段階では）気にしなくていい」ということをお子さまに繰り返し強調する、というのが、次善の策ということになるでしょう。

何度も繰り返しになりますが、分数・小数の学習は「新しい世界に入っていく」入口です。「わからないこと」「つまずいてしまうこと」があるのは、いわば当然の話です。むしろそこで「わからないこと」とじっくり向き合い、今まで「わかった」つもりでいたことについての理解を深めていったり、新しい概念を獲得したりする経験ができれば、それはその先の算数・数学を進めていく上での貴重な財産となるでしょう。保護者の方々をはじめ、周りの大人の皆さまには、焦ることなく、焦らせることなく、カベを越えていこうとする子どもを温かく見守り、応援してあげてほしいと思います。

---

いかがでしょうか。

　まだまだたまに気温の低い日もありますが、少しずつ夏には近づいてきているようで、少し暑さを感じる日も増えてきましたね。そういう日は最近、アイスを食べたりもしています。昔は安くて量が多くて大味なアイスばかり食べていたのですが、年齢を重ねてくるにつれて、繊細な味のアイスも嗜むようになりました。そういう視点でいろいろと見てみると、各社、工夫を凝らしたアイスをたくさん出しているのですね。今年の夏はいろいろとアイスを食べ比べてみたいものですが、そのためにもまずしっかり運動をしないといけません。以前から運動するする言っておきながら、なんだかんだで全然動いていないのですが、今月こそはがんばりたいと思います。

　それではまた来月！