学ぶにつれて好き嫌いや得意・苦手が分かれがちな算数。苦手に感じているお子さまも、「好き」「得意」というお子さまも、夏休みを迎える今、学校で学ぶ算数から少し離れて、身近なところから算数のおもしろさを感じてみませんか? 算数・数学のおもしろさを伝える講演活動をされているサイエンスナビゲーター(R)の桜井進さんに、算数が「嫌い」「苦手」なお子さまでも「おもしろいかも!」と思える身のまわりの「数」「形」「計算」の楽しみ方を教えていただきました。(取材・文 浅田夕香)
※本記事は、2021年7月22日に「Z-SQUARE」上で掲載した記事を一部修正の上、再掲しています。
算数は、身のまわりにあふれている
――桜井さんは、講演活動やご著書を通じて身のまわりのものから算数を楽しむための視点を発信されています。算数を「楽しむ」という感覚がもてずにいる小学生も多いと思いますが、桜井さんなら、そんな小学生にどんな話をされますか?
たとえば、漢数字の「十」には「つなし」という読み方があり、名字にも使われていますが、なぜ「つなし」と読むかご存じですか?
ヒントは、数の数え方にあります。1から9までは「ひとつ、ふたつ、みっつ、……ここのつ」 と「つ」が付きますが、10はどうでしょうか?「とお」で「つ」が付きませんよね? このことから、「つなし」と読まれるようになったと言われています。また、「一」を「にのまえ(2の前)」と読んだりもしますし、漢数字はおもしろいですね。
――漢字の読み方の由来に数の数え方が関係しているんですね。
そうなんです。ほかにも九十九(つくも)や八百万(やおよろず)などおもしろいものがいろいろあるので……、調べてみてください。
もう1つ、九九のマジックを紹介します。九九の九の段の答えは、両手の指10本で出せるんですよ。
――??どういうことでしょうか?
たとえば、「9×3」の答えを知りたいときは、両手を開いて左から3本目の指(左手中指)を折ります。すると、その指を境に左側には指が2本、右側に7本の指が立っていますよね? 左側の指の本数が十の位、右側の指の本数を一の位と考えると、2と7で27。9×3の答えと一致します。同じように、「9×1」の場合、左から1本目(左手親指)を折ると、左側0本、右側9本で答えは9。
「9×2」だと、左から2本目(左手人差指)を折るから、1本と8本で答えは18。
「9×4」だと、左から4本目(左手薬指)を折るから、3本と6本で答えは36。
「9×9」だと、左から9本目(右手人差指)を折るから、8本と1本で答えは81。
「9×10」だと、左から10本目(右手親指)を折るから、9本と0本で答えは90。……という具合に、九の段は指を折るだけで答えを出せるんです。
――これは驚きです! 考えてみたことがなかったです。
九の段の答えをよく見てみてください。「9×1=9」から「9×10=90」まで、1の位が「9、8、7、……3、2、1、0」と1つずつ減っているでしょう? さらに見ていくと、答えの十の位と一の位を足すと、「0+9」「1+8」「2+7」……「8+1」「9+0」と、すべて9になることがわかります。だから、指を折ると答えが出る、というマジックをつくることができるんです。おうちの方がお子さまに「ねえ、こんなの知ってる?」とやってみせることで、お子さまは楽しい気持ちで九九に触れ、九九のヒミツを知ろうと思ってくれるのではないかと思います。これはほんの一例ですが、身のまわりには、数や形、計算に関連づけて楽しく考えられる題材がたくさんあります。夏休みはまさに身のまわりの算数を楽しむチャンスです。算数を勉強するのではなく、算数を楽しむ時間をぜひつくってほしいですね。
――「算数を楽しむ」というのは、学校の勉強からはなかなかイメージしづらいように思います。
学校の算数とは少し切り離してとらえるといいですよ。英語に、「do math」という表現がありますが、日本語に訳すと「数学をする」で、能動的になんでも数学で考えてみることを表します。音楽やスポーツ、ダンスに「自分がプレーヤーになる」「人のプレーを観戦する」などさまざまなかかわり方があるように、数学や算数も「学校で授業を受ける」だけでなく、「能動的に何でも数学で考えてみる」というかかわり方もできるはずなのです。
たとえば、ピザのように丸いものを「人数分、同じ大きさに切り分けるにはどうしたらいいだろう?」と考える、ミートボールをお兄ちゃんは5個食べて、自分は3個しか食べられなかったところから「同じだけ食べるにはいくつといくつに分ければよかったんだろう?」「あと何個あったら同じだけ食べられたんだろう?」などと考える。このようにして日々の生活を数学・算数の視点で見ていくことも「do math」です。そうやって、身近にある数や形からお子さまの「なんでだろう?」が出てくるよう、保護者の方が身構えずに、お子さまとコミュニケーションをとっていけるといいですね。
――桜井さんご自身も、幼いころから身のまわりの事象を算数・数学で考えていらっしゃったのでしょうか?
そうですね。ぼくの場合、入り口はラジオでした。ラジオを聞くのが好きで、聞くことが高じて「ラジオを作りたい!」と思ったんです。ラジオを作るには、電子回路を設計しないといけなくて、そのためには数学が必要だということに10歳で気づき、ラジオ・音響技能検定を受けたり(現在は検定試験休止中)、関数電卓を買って、「√」や「π」と書かれたボタンを「これってどういうことだろう?」と触ってみたり、知り合いのお兄ちゃんから中学・高校の数学の教科書を借りて必要なところだけかじったりしていきました。
チューニングを表す公式にf=1/2π√LC(2π√LC分の1)というものがあり、意味がわからないまま覚えて、ラジオを設計して、形にしたら、本当に計算通りにラジオから音声が流れた!という体験がぼくの原点です。「ほんとに動くんだ! 数学ってすごい!」と衝撃を受けました。この経験から、「なんでこの公式ができるんだろう?」と数学に興味を持ち、より深く探究して、わかって、驚いて、の繰り返しで現在に至ります。
ぼくにとって数学は、「ダンスを踊れるようになりたいから踊れるまで練習する」「シュートを決められるようになりたいから決めるまで練習する」ことと同じだったんですよね。わからない公式をあと10年たったら理解できるだろうと思いながら見ているだけで楽しかったですし、先ほどご紹介した九九のマジックなんかも小学校のときに自分で見つけていたんですよ。学校のテストや、先生・親からの注意におびえながら学ぶのではなく、「知りたい」「作りたい」から探究する。すると、必要な知識がどんどん頭に入っていくんです。いま小学生のみなさんにも、身のまわりにある算数のワクワクを見つけて、楽しんで数や形について知っていってほしいと思います。
夏休みに体感!日常のなかにある算数の例
――では、実際に、日常のなかにある算数のおもしろさを体感するには、どんなことに着目したり、実践したりするといいでしょうか?
そうですね、例をいくつかあげますね。
買い物で
- 購入する商品の合計金額をどちらが早く計算できるか競争する
- 「30%OFF」「10%増量」などの表示から、どれだけ価格がお得になっているのかを計算する
- 同じ種類の2つの商品のどちらがお買い得かを判断するのに「1グラムあたり何円か」という単位量当たりの価格に注目してみる
このようなかたちで、価格表示からいろいろな計算にトライすることができます。とくに、比や割合の計算は、机上ではなかなか理解しづらいので、実生活で使う計算なんだということを見せてあげることがとても大事です。
ガソリンスタンドで
- 1リットルあたりの価格と、車に入るガソリンの量から、「ガソリンを満タンにするといくらになるでしょう?」と問題を出す
1リットルあたりの価格が書かれた看板に注意をうながして、「あれって何のことだと思う?」とたずね、「146円って書いてあるよ」「そう、ガソリン1リットルが146円なんだ。うちの車は50L入るんだけど、満タンに入れるといくらになると思う?」「ガソリン2,000円分だと何リットルになるかな?」などとお話ができるとといいですね。
地図を使って
- 「縮尺をもとに、自宅から駅までの距離を計算してみよう」「1分で歩ける距離は○メートルだから、自宅から駅まで何分で行けるか計算してみよう」などと問題を出す
地図は、比や時速と距離・時間の関係について理解を深められる題材です。掛け算を知っていれば、低学年でも取り組めますよ。
6年生くらいになれば、地図の図法の種類を紹介するのもおすすめです。「メルカトル図法」「モルワイデ図法」「正距方位図法」など、地図の図法にはさまざまなものがありますが、球面を平面で表すうえで何を正確に表現し、何を犠牲にしているのか、その過程にどのように数学が関与し、発展したかを知り、考えるきっかけになります。
定規やコンパスを使って
- 低学年のお子さん:デザイン定規でさまざまな模様をかく
- 高学年のお子さん:コンパスと分度器で正五角形をかく
100円ショップなどで購入できる円の中で歯車をまわすスピログラフ定規(デザイン定規)を使ってできる模様って、美しいですよね。
 円という図形自体の美しさ、円の周期的な動きを繰り返すことで生み出される模様の美しさなど、美しいものを美しいと感じることも算数・数学への関心につながります。低学年のうちは「きれいな模様がかけたね」とお子さまと一緒に楽しんでみてください。ちなみに、デザイン定規によってつくられる模様は、高校数学で学ぶsin(サイン)・cos(コサイン)で説明できるんですよ。
円という図形自体の美しさ、円の周期的な動きを繰り返すことで生み出される模様の美しさなど、美しいものを美しいと感じることも算数・数学への関心につながります。低学年のうちは「きれいな模様がかけたね」とお子さまと一緒に楽しんでみてください。ちなみに、デザイン定規によってつくられる模様は、高校数学で学ぶsin(サイン)・cos(コサイン)で説明できるんですよ。
高学年になったら、正五角形をコンパスと分度器でかいてみるのもよいでしょう。手順を説明しますね。
まず、円をかいて、半径を一本引きます。円の中心の周りの角360°を五角形なので五等分するんですね。360°÷5=72°となりますので、最初に引いた半径から分度器で計って72°のところに中心から円周にむけて線を引きます。いま引いた線からまた72°になる線を分度器ではかって中心から円周へ線を引きます。これを繰り返し、5本の半径を引きます。5本の線と円周が交わったところが正五角形の頂点になりますので、5つの頂点を結ぶと正五角形がかけます。これができたら、コンパスと定規だけで正五角形をかく方法もあるので、調べてチャレンジしてみるのもいいでしょう。
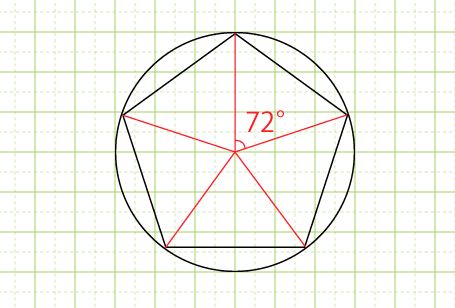
やってみると自分の手でかけることに感動します。実際にいろいろな多角形をかいてみることで、角度についての興味がわきますし、コンパスや分度器という使い方にコツが必要な道具をうまく使えたことに対する喜びも、図形や算数への関心につながるでしょう。
時計を使って
- 時計はなぜいちばん上が「12」なのか?
- 数は10でひとまとまり(十進数)なのに時計はなぜ違うのか?を考えてみよう、と問いかける
まず、アナログの時計の文字盤が12でなく10で分割されていたらどうなる?と考えてみましょう。10分割だと、10の約数は2と5しかないので、3分割、4分割ができず、2分割、3分割、4分割、6分割ができる12に比べて不便なんですね。それが、12で刻まれている理由のひとつです。
1時間は60分ですし、円は360度なので12できれいに分けられる数です。実際に時計を10等分で表そうとすると12で分けられている意味がわかってくると思います。ぜひやってみてください。
じつは、ピアノの1オクターブも白鍵と黒鍵を合わせると12なんですね。12という数は便利な数なので、ほかにもどんなところに使われているか考えてみるのもいいでしょう。12について考えていくと約数や倍数に触れることもできます。
フィボナッチ数列の不思議
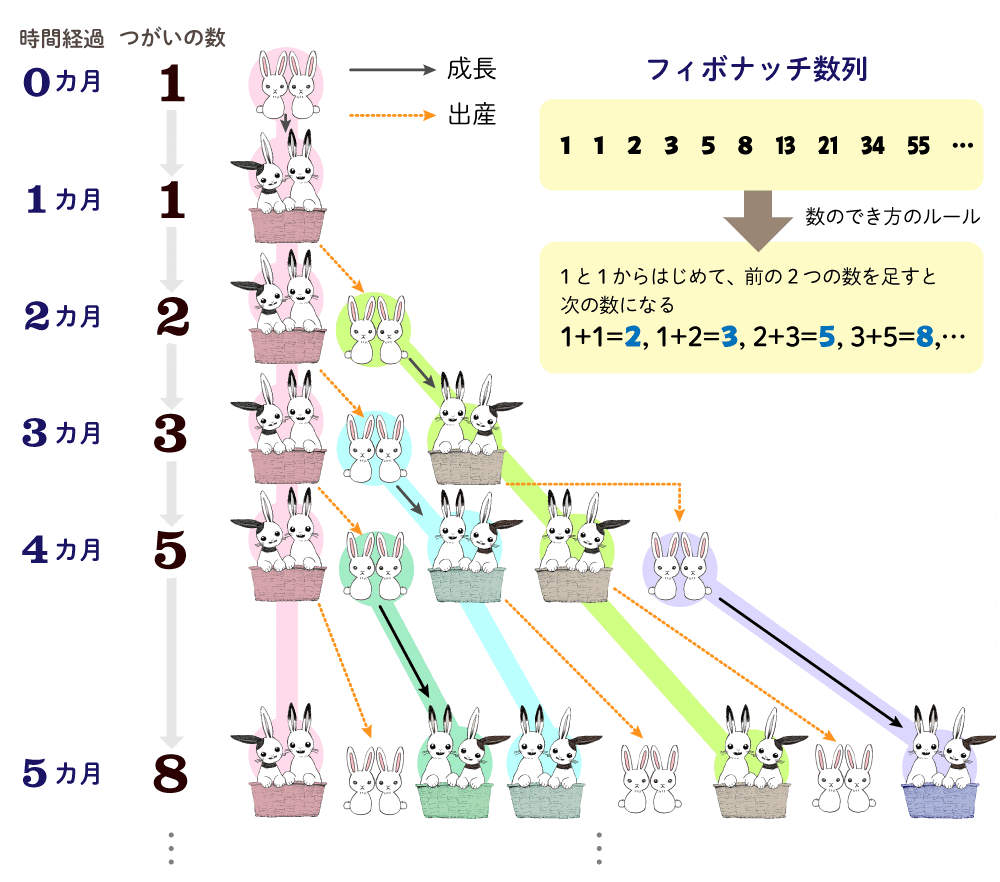
みなさんは、フィボナッチ数列をご存じでしょうか。聞いたことはあるかもしれませんね。フィボナッチ数列は、植物から宇宙まで、自然界のいたる所に見つかる不思議な数列です。「花びらの枚数」や「松ぼっくりの鱗(うろこ)模様の数」、「ひまわりの種の数」などがあてはまります。
この数列は数学者のフィボナッチが「ウサギの増え方」を考えることで、発見したのだそうです。子ウサギを観察したところ、1カ月後には大人(1つがい)になり、2カ月後には子ウサギを産んで2つがいになりました。3カ月目には3つがい、4カ月目には5つがい、5カ月目には8つがい、ウサギは「1,1,2,3,5,8,13,……」と増えることに気がついたそうです。
身近なものの例として、木の枝の伸び方もフィボナッチ数列で説明できるタイプのものがあります。木の枝は成長期に2つに分かれます。枝が2つに分かれるときに栄養は均等に配分されるわけではないので、栄養の多い枝と、少ない枝に分かれます。栄養の多い方の枝は次の成長期に、栄養の少ないほうの枝は次の次の成長期に2つに分かれるといった感じで伸びていきます。この枝分かれの様子を図に表すと下図のようになります。おのおのの成長期における枝の本数はフィボナッチ数列として説明できます。
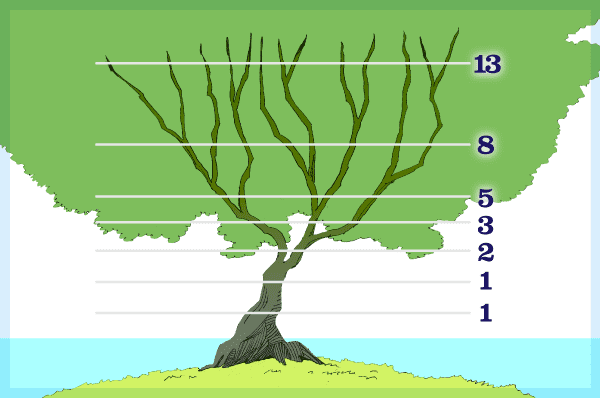
フィボナッチ数列はいろいろなところで確認ができますので、興味を持たれた方はお子さまと一緒にさがしてみてもよいでしょう。
このように自然界にある現象の背後に算数で説明できるルールが見つかります。そのことを自分で調べたり確かめたりすることで算数というものの存在に興味・関心を持つことができるようになります。
「素数ゼミ」からわかること
先日ワシントンD.C.をはじめとするアメリカ東部地区で、17年ぶりに「素数ゼミ」が数十億から数兆匹現れた!とのニュースがありました。TVなどでご覧になった方もいらっしゃるかもしれませんね。200万年前の氷河時代、寒さに耐えかねたセミたちは地中にもぐって生きるようになりました。寒い氷河時代でもあまり気温が下がらない場所があったのでそこでセミたちは生き残りました。とはいえ気温は低いのでアメリカ北部のセミたちは14〜18年もの長い間地中で過ごすようになりました。
たとえばある年に15年と18年周期のセミがいっしょに地上に出て子どもをつくったとしましょう。15年後に15年ゼミが、18年後に18年ゼミが地上に出てみたら、他の周期のセミが地上にはいないので子どもをつくれずにセミの数が減ってしまう。さらに、15年セミと18年セミの間にできた子どもの周期は16年や17年となってしまい周期が乱れてしまいます。結局、90年ごとに繰り返す15年セミと18年セミの出合いは双方にとってよくない結果を生み、何万年も経てばどちらも絶滅してしまうのですね。違う周期同士のセミはなるだけ地上で出合わない方が生き延びることができるということなのです。そこで14年、15年、16年、17年、18年の5種類のセミたちの中から2種類のセミ同士が出合う周期(最小公倍数)を求めてみると次のようになります。
素数17と18(=2×3×3)の最小公倍数17×2×3×3=306
素数17と15(=3×5)の最小公倍数17×3×5=255
素数17と16(=2×2×2×2)の最小公倍数17×2×2×2×2=272
15(=3×5)と16(=2×2×2×2)の最小公倍数2×2×2×2×3×5=240
16(=2×2×2×2)と18(=2×3×3)の最小公倍数2×2×2×2×3×3=144
15(=3×5)と18(=2×3×3)の最小公倍数2×3×3×5=90
15年セミと18年セミは90年ごとに出合うのに対して、17年セミと18年セミは306年ごとに出合います。素数が周期の17年ゼミが入ると最小公倍数は大きくなることがわかります。つまり周期が異なるセミと出合いにくいということです。何万年、何十万年も経つうちに最小公倍数の小さい周期のセミは減っていき、最小公倍数が大きいセミだけが生き残っていきました。これが17年周期の素数ゼミが今も生き残っている理由です。最小公倍数が小さい方が頻繁に地上で出合ってたくさん子どもを残せるから生存には有利と思いきや、それとは逆なんです。できるだけ出合わない方が結局生き延びることができたということです。
このように身近なものごとを算数としてとらえ、計算のしかたを考えたり法則性を見つけ出したりすることで、お子さんの算数への興味がぐっと広がっていくと思いますので、ぜひ親子で日々の生活を楽しんでいただければと思います。
算数を楽しむには
――最後に、算数を楽しむためのコツを教えてください。
3つあります。1つ目は、「勉強(無理してがまんしてすること)しないこと」。「勉強しなきゃ」「テストで点を取らなきゃ」ではなく、「知りたい」という気持ちから探究していく。その状態になることが、算数を楽しむコツのひとつです。「なぜだろう?」「どういう規則性でこうなるんだろう?」などと、疑問をもち、調べることや考えることに没頭する。そうすると、それは勉強ではなく探究になります。
2つ目は「わかるまでやること」、3つ目は「人と比べないこと」です。人と比べずに、本人のペースで、わかるまで調べ、考える。これら3つは、音楽やスポーツ、ダンスなどにも当てはまります。算数も同じで、これら3つを実践すれば、どんどん算数に興味・関心を持つようになっていきます。
そうして探究するなかで、世のなかのさまざまな事象が何かしらの法則や規則性にのっとって成り立っていることを知れば、ますます算数がおもしろくなります。
その際に気をつけたいのは、おうちの方もお子さんと一緒におもしろがること、そして強制しないことです。「これって何だろうね?」「なんでこうなるんだろうね?」など、さりげなく質問を投げかける。そして、すぐに答えを教えるのではなく、お子さんが調べたり考えたりするのに根気よく付き合う。じっくりと考えたり、調べたりするって楽しいんだ、とお子さんが感じられるように、お子さんのペースに合わせて取り組んでくださいね。
夏休みに身近なものを算数で考えることを通して、ぜひおもしろさに気づいていただければと思います。
――ありがとうございました。

桜井 進(さくらい・すすむ)
サイエンスナビゲーター(R)。株式会社sakurAi Science Factory 代表取締役CEO。東京理科大学大学院非常勤講師。1968年山形県生まれ。東京工業大学理学部数学科卒業、同大学大学院社会理工学研究科博士課程中退。大学在学中から予備校講師として教壇に立ち数学や物理を楽しくわかりやすく生徒に伝える。2000年にサイエンスナビゲーター(R)を名乗り、数学の歴史や数学者の人間ドラマを通して数学の驚きと感動を伝える講演活動をスタート。
小学生からお年寄りまで、誰でも楽しめて体験できる数学エンターテイメントは日本全国で反響を呼び、テレビ・新聞・雑誌など多くのメディアに出演。著書は『親子で楽しむ! わくわく数の世界の大冒険』(日本図書センター)、『考える力が身につく! 好きになる 算数なるほど大図鑑』(ナツメ社)など50冊以上。

