「お子さまに寄り添った添削」「充実した解説」を日々お届けしている通信教育のZ会が、2023年度開成の入試問題「算数」を詳細に分析しました!
入試問題の概観と大問1つを厳選し、Z会ならではの視点で解説をまとめましたので、ぜひお役立てください。
入試概観・解説(開成中学校)
開成中学校の算数を徹底分析!今年の入試問題の概観と、開成中ならではの問題「大問2」の詳細解説を掲載。複数の解法を紹介しますので、解いた人は自分の解法に合わせて、まだ解いていない人は自分に合った解き方をご確認ください。
概観
入試問題全体を通して
例年より大問数が1題増え、大問5題構成となった。3~4題の前提で時間設定を訓練してきた受験生の中では、戸惑った人も多かったのではないだろうか。
ただ、各問の難度は例年に比べてかなり易しく、開成を受験する生徒であれば手が止まることはほぼなかったと思う。
学校からの発表によると、合格者平均点は9割近い。(85点満点中76.4点)高得点での争いになったため、出題された各分野のうち1つでも苦手分野があった場合、算数においてはとても厳しい戦いになったと思われる。当然、細かな見落とし、単純な読み間違い、計算ミスなどケアレスミスは許されない試験であった。
今年は格段に易しかったため、今年の出題を基準にして開成対策を行ってはならない。未来の開成受験生たちは、ぜひ過去問を数年分解いてみてほしい。難しい年の難度であっても太刀打ちできるように、算数の難問対策を強化しておこう。
大問1
『ウサギとカメ』を題材にした速さの問題。卯年だからだろうか。寓話に忠実な展開である。
最難関校の速さの出題としては珍しく、比を使わずに解くことができる。ウサギとカメの速さの差が大きいため、比率が正確なグラフはかきにくい問題ではあった。
速さの問題としては標準的なレベルなので、合格するには正解しておきたい1問。
大問2
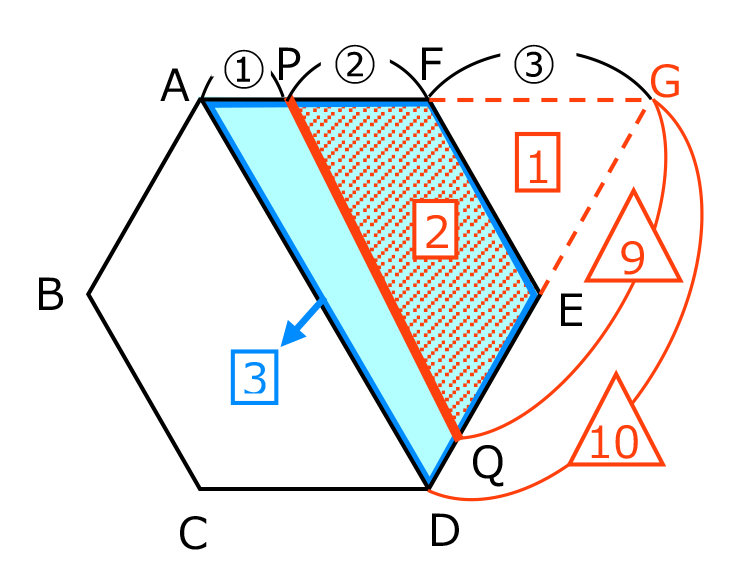
正六角形の分割の問題。今後応用問題に出会ったとき、いろいろな観点から解法を模索できるよう、複数の解法を掲載する。
六角形を題材とした出題は辺の長さが明記されても面積が求められないため、面積を考える際に比を使うことが大前提となる。
Z会『頻出分野別演習』平面図形難問対策でも、このような六角形の問題の扱い方を取り上げている。辺の比や面積比を扱う問題として六角形は最難関校で扱われやすいため、演習を重ねておこう。
大問3
立体の切断は開成では頻出。今回の問題は2回切断しているが、できあがった形がわかりやすく、体積を求める方針も立てやすかったのではないかと思う。
(1)の見取図は基本的な出題だが、普段自分で立体を図示するときに切断面の交線を意識し正しくかけているかが問われる。
(2)は、問題文の中で2つの三角柱の共通部分をかなり大きく図示されていたので取り組みやすかっただろう。
立体の切断は今回の問題よりもかなり難しい出題が、例年の開成や最難関校で多く出題されている。Z会『頻出分野別演習』立体図形難問対策などで、切断の多様な出題に慣れておく必要があるだろう。
大問4
(1)を答えたとき、すぐに規則性に関する問題だと気づけただろうか。周期のおおもととなる最初の6秒がこの問題の要となるので、6秒間の3点の動きは面倒がらずに丁寧に把握しておくべきだろう。他の点と出会うと向きが変わる不規則な動きをするので、1~6秒の1秒ごとの各点の位置を図示したほうが勘違いしづらく、6秒間で2点の出会う回数が点Qと点Rの組み合わせだけ多いことも気づきやすい。
周期算や日暦算などの周期性・規則性の問題は、あまりの扱いなどを勘違いしたときに、その間違いに気づきにくいのが特徴だ。時間に余裕がある場合は、落ち着いて問題文の条件や立式と計算、自分の考えた周期の内容を確認し、何か見落としていなかったか、勘違いをしていないかを確認するとよいだろう。
大問5
1~7の数字だけを使ってできる数を用いた場合の数の問題。設定は難しめだが、解法をほぼ問題文の中で明かしてくれているため、問題文が導く通りに解けばつまることはないだろう。
(1)を使って(2)を、(2)を使って(3)を、……と出題内容が密接につながっているため、(1)を間違うとほぼ全部間違ってしまう。しかし問題文に書かれている説明が今までの出題ではありえないほど丁寧だったため、「本当にこれで合っているのか?見落としていないか?」と戸惑った人もいただろう。問題文にある「これ(ら)を参考にして考える」とはどういうことだろうか、と出題者の意図を汲み取っていくことが重要である。
大問2の解説
大問2「正六角形の分割」は、図形的見地・関数的見地の複数の視点から解くことができる問題だった。今後、平面図形の応用問題に取り組んでいくうえで、身につけておくとよい発想が得られると思うので、ぜひ別解もふくめ確認しておこう。
2分10秒後、3分12秒後
《着眼》
・内部を 6つの合同な形に分けられる。
・外側に正三角形を補うと大きな正三角形ができる。
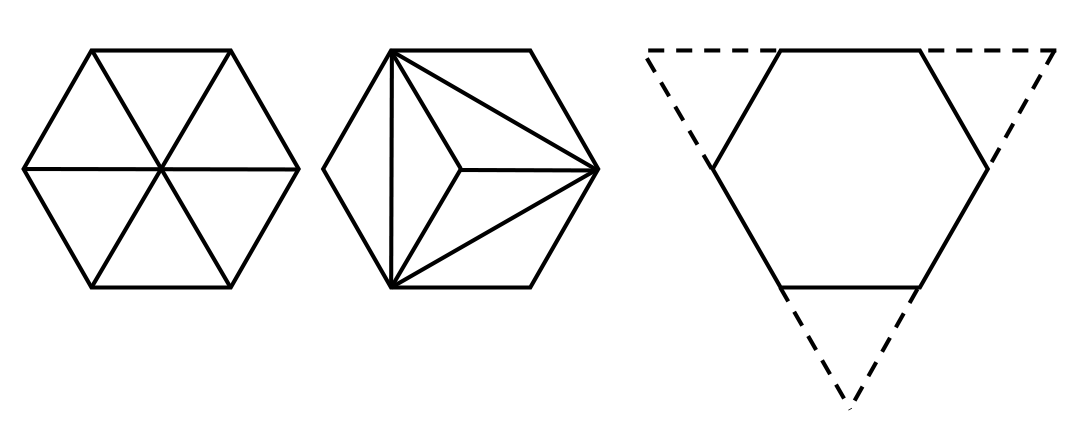
・面積の変化をグラフに表す。
という解き方に出会ったことがある人も多いだろう。
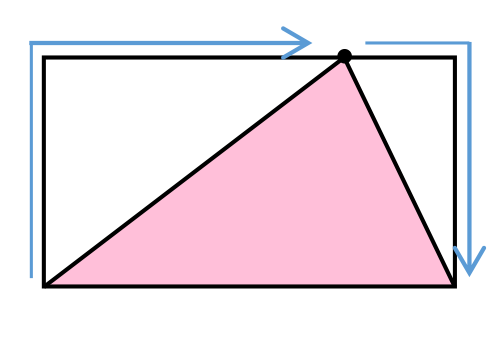
今回は、大問2について、以下の3通りの解法を紹介しよう。
1.正六角形の内部を分割する
2.外側に補助線を引く
3.グラフを用いる
解法共通の準備
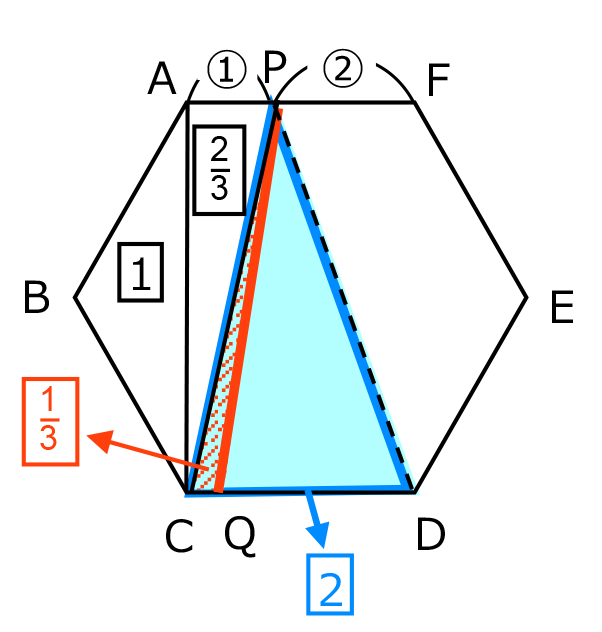
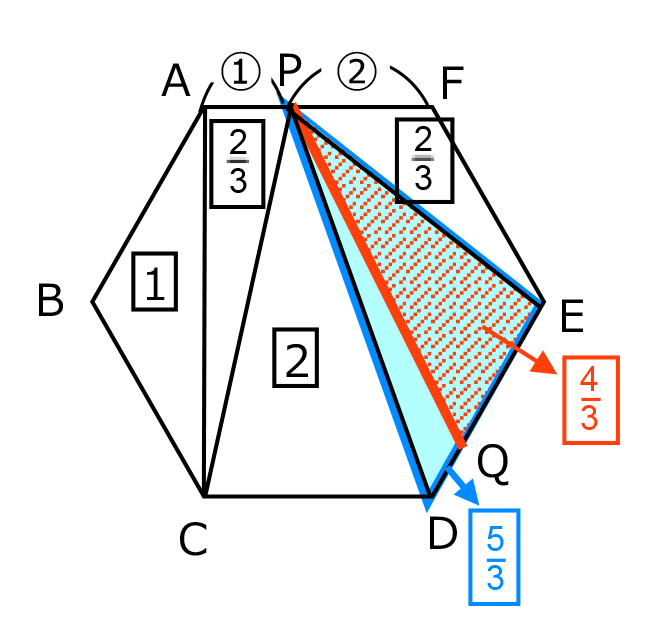
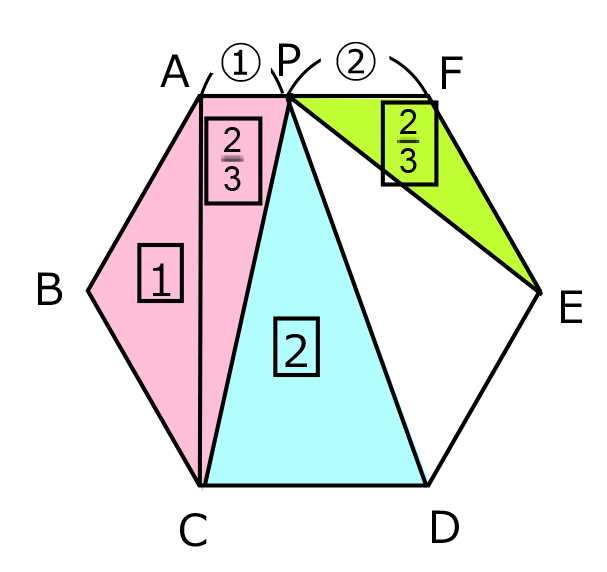
【正六角形の各部分の面積と前提】
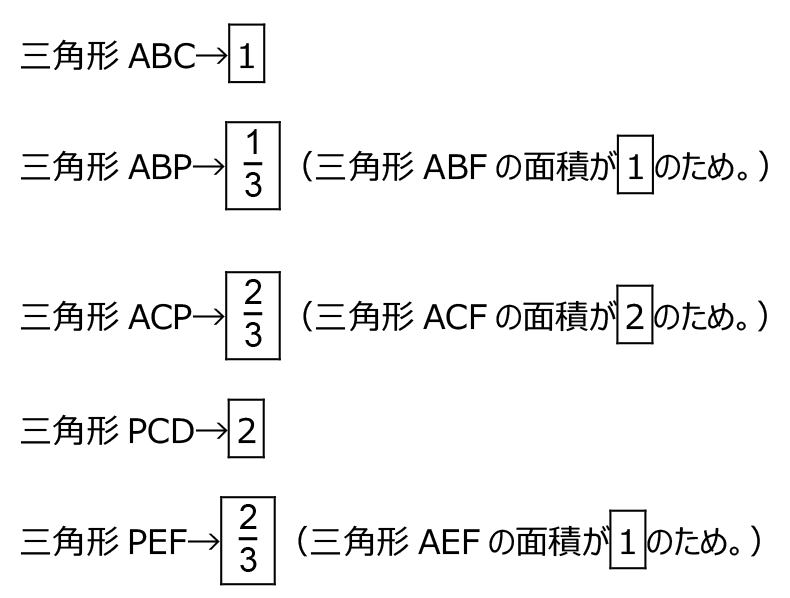
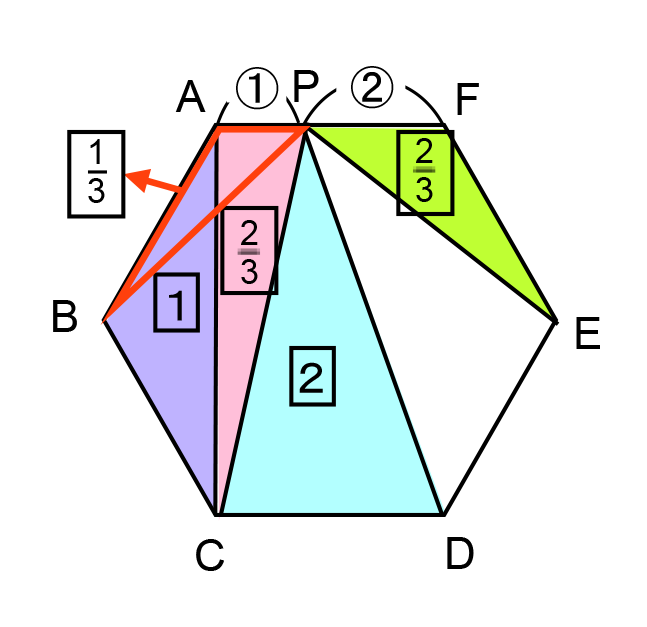
正六角形 ABCDEF の面積を6とする。(正六角形は内部を 6 分割できるため6とおいたが、全体を1とおいてもよいし、別の数をおいても問題ない。)
この正六角形を直線 PQ で分けたとき、片方の面積が2または4となればよい。
解法1.正六角形の内部を分割する
面積が6の正六角形 ABCDEF を直線 PQ で分けたとき、片方の面積が2または4となればよい。
三角形 ABC の面積は1、三角形 ACP の面積は
 だから、点 Q は辺 CD 上にあり、三角形 PCQ の面積が
だから、点 Q は辺 CD 上にあり、三角形 PCQ の面積が となるときに、左側の面積が2となる。
となるときに、左側の面積が2となる。三角形 PCD の面積は2だから、三角形 PCQ と三角形 PQD の面積比は、
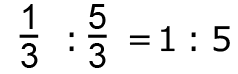 となり、
となり、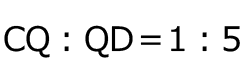 とわかる。
とわかる。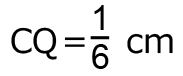 より、
より、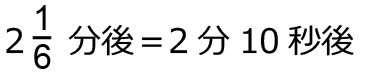
●右側の面積が2となる場合
正六角形の内部の面積は次の図のようになっているから、点 Q は辺 DE 上にあり、三角形 PQE の面積が
 となるときに、右側の面積が2となる。
となるときに、右側の面積が2となる。三角形 PDE の面積は
 だから、三角形 PDQ と三角形 PQE の面積比は、
だから、三角形 PDQ と三角形 PQE の面積比は、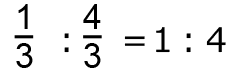 となり、
となり、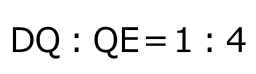 とわかる。
とわかる。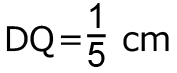 より、
より、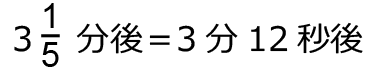
解法2.外側に補助線を引く
正六角形 ABCDEF の面積を6とし、「●左側の面積が2となる場合」は【解法 1;正六角形の内部を分割する。】と同様。
「●右側の面積が2となる場合」について、次のように求めることができる。
次の図のように補助線を引くと、三角形 ADG の面積は4、三角形 PQG の面積は3となる。
三角形 FEG は正三角形だから、
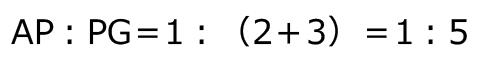
三角形 ADG と三角形 PQG の面積比から、
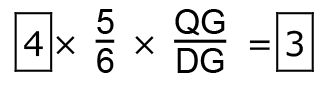 つまり、
つまり、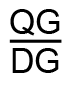 は、
は、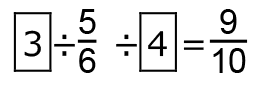
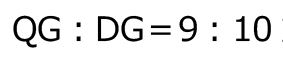 だから、
だから、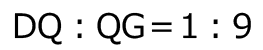 で、
で、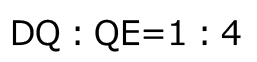
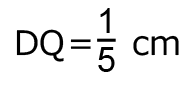 より、
より、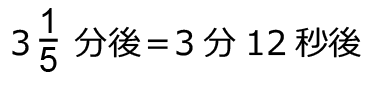
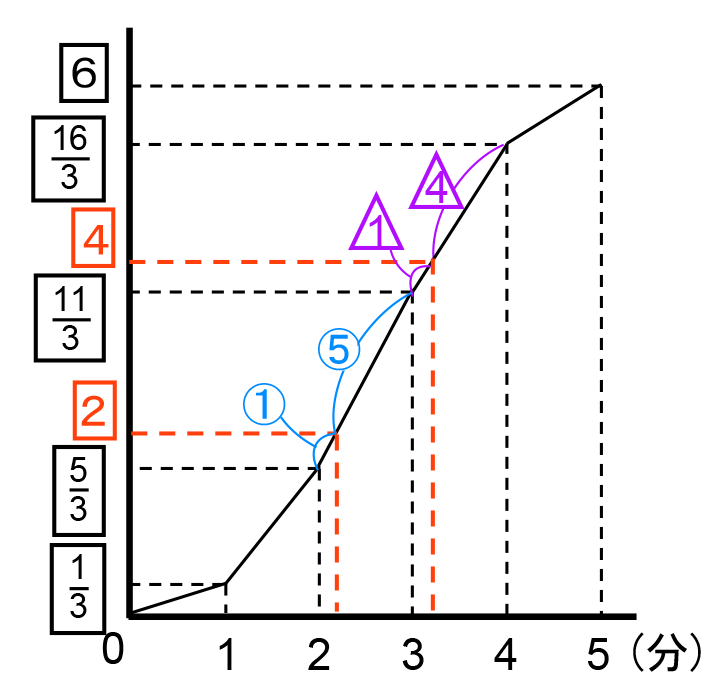
解法3.グラフを用いる
面積が6の正六角形 ABCDEF を直線 PQ で分けたとき、片方の面積が2または4となればよい。
頂点 B → 三角形 ABP だから、
頂点 C → 四角形 ABCP=三角形 ABC+三角形 ACP だから、
頂点 D → 四角形 ABCP+三角形 PCD だから、
頂点 E → 正六角形-三角形 PEF だから、
点 Q が出発してからの時間と左側の面積をグラフで表すと右のようになるから、
2になるのは、
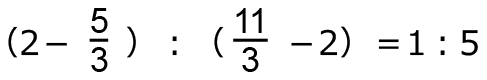 より、
より、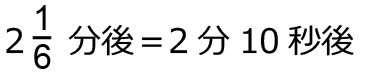
4になるのは、
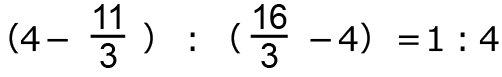 より、
より、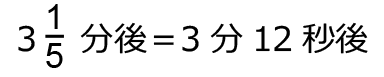
グラフが直線になるのは、点 Q が辺 CD 上にあるときは三角形 PCQの面積、点Q が辺DE上にあるときは三角形 PDQ の面積について、高さが一定で、底辺の長さだけが一定の割合で増えていくためである。
グラフによる面積の変化を利用すると、各頂点を通るときの面積を最初に調べておけば、そのあとは作業として解ける。
非常に便利なので、Z会頻出分野別演習「平面図形難問対策」などで、実戦的に使えるよう演習しておこう。
【開成対策に!】Z会の専科講座【算数】
3か月完成(毎月1回のお届け)の「Z会中学受験コース 専科」。塾での学習と並行しても負担の少ない教材量で添削指導までついており、通塾の方にもプラスオン教材としておすすめです。
「頻出分野別演習」の他にも、開成中学を想定した予想問題をお届けする専科「志望校別予想演習」、超難問群に取り組む「最難関中学受験プレミアム講座」などもございます。今の学習状況・やりたいことに合わせてご受講ください。
「Z会 筑駒・開成受験応援LINE」のご案内

