「お子さまに寄り添った添削」「充実した解説」を日々お届けしている通信教育のZ会が、2024年度開成の入試問題「算数」を詳細に分析しました!
入試問題の概観と大問1つを厳選し、Z会ならではの視点で解説をまとめましたので、ぜひお役立てください。
入試概観・解説(開成中学校)
開成中学校の算数を徹底分析!今年の入試問題の概観と、開成中ならではの問題「大問3」の詳細解説を掲載。
大問3の解説だけにとどまらず、他の入試問題を解くときにも活かせる立体図形のポイントも紹介しますので、ぜひご確認ください。
概観
入試問題全体を通して
昨年は大問5題で、各分野からまんべんなく出題してくる形式であったが、今年は大問3題。「速さ」の出題はなく、大問は「場合の数」と「立体」からの出題であった。
大問1が小問集合となっているのは2022年度・2021年度と同様であり、大問3題の形式は2021年度以来である。
ほとんどの問題が開成らしい個性的な出題で、事前に類題に取り組み備えられた受験生は少数派だっただろう。
ただし、例年の開成よりも誘導の見せ方がかなり丁寧になっており、(1)(2)を解くことで後半の解き筋が見えやすくなる。
初見の問題における「(1)はいったい何を確認しているのか」といった出題意図を読む能力が、かなり有利に働く入試だったと思われる。
大問1
入試の開始直後に(1)の問題文を見て、とまどった受験生は多かっただろう。問題文の中で試験の得点に言及する算数の問題はなかなか見られない。
最小パターンの検討には時間がかかるため、とりあえず1パターン作ってみて、より使う数字の個数が少ないものを考えるのは他の問題を見てから…という作戦が現実的だろう。
(2)は「切り取る長さが34.5cmのときだけ」重さが等しくなる、という条件が大事になってくるが、この条件の読み替えはさまざまな問題に解き慣れないと思いつくことが難しい。とくに(イ)で苦戦した受験生は多かったのではないだろうか。開成のバラエティ豊富な出題の対策として、一度は解いておきたい問題といえる。
(3)の正三角形の回転移動は、他よりも受験生にとっては馴染みのある問題だったはずだ。得点源となるので、「頂点の動き」「正三角形の通過部分」の違いに注意しながら丁寧に正解を導いておきたい。
大問2
数のカードと操作の問題。長文の問題だが、(1)で操作内容、(2)でカードが増えたときの考え方を確認しており、(2)の考え方を利用していけば、(3)で正解を導き出すのはそれほど難しくない。
しっかり長文を読みこなし、誘導の意図を汲み取ることで解法をすっきりと整理できる、受験者の算数的読解力と場合の数の本質理解が正しく問われる問題であった。
大問3
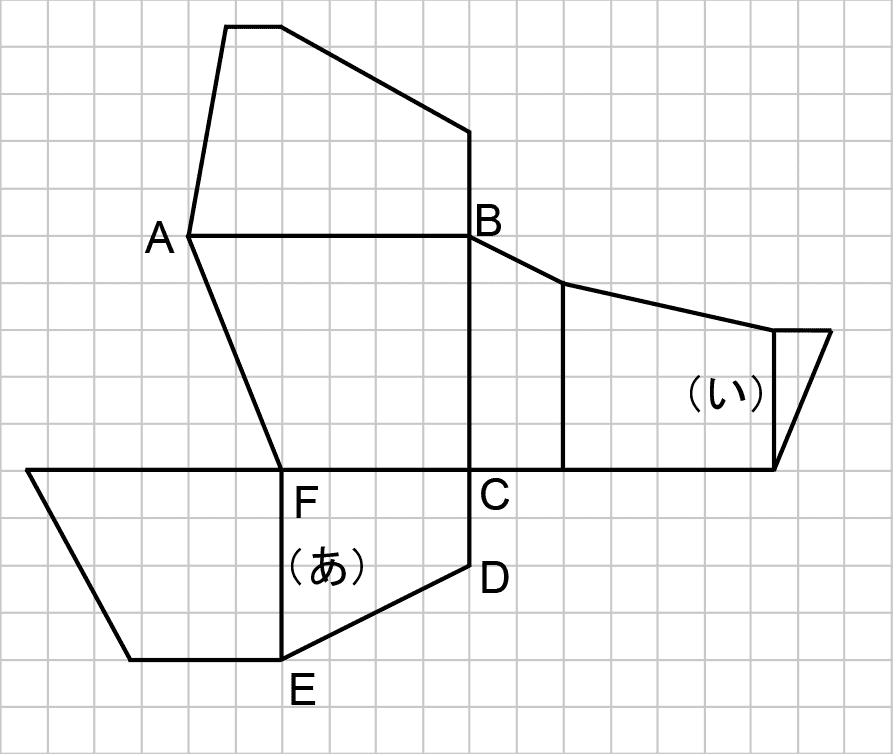
直方体を3回切断したあとの1つの立体の展開図から切断のようすを紐解くという設定で、立体分野を得意としない受験生はかなり警戒しただろう。
ただし、問題文中の複雑そうな設定に対して、展開図を見るとそれほど想像しにくい形の立体ではない。頂点A、B、Cが見取図にも展開図にもかきこまれているので、(1)(2)…と順に解いていくことで、立体が切断前の直方体の中にどのように収まっているか把握しやすいようになっている。
以下に解説を掲載するので、「なんとなく」想像していた形がどういった論拠で確定しているのかを含め、確認してほしい。
(2)(3)(4)は解答用紙の図内に図示する問題となっており、どの問題でも「なるべく正確に」かくよう問題文中で注意されている。
立体図形の問題においては、立体内のようす、表面上の切断線のようす、切断面内のようすなどを自分で図示して考えることが必須となるが、そういった際に「辺上の点を、指定の比で辺を分割するような位置にとれているか」「直線をフリーハンドでまっすぐな線で表現できているか」「垂直な2本の直線、平行な2本の直線がそうとわかるようにフリーハンドで表現できているか」を普段から心がけて丁寧に行えているかが問われる。
これらの描く力は立体図形・平面図形の問題を解く上での大きな地盤になるので、日々の演習を重ねるうえでぜひ磨いていってほしい。
開成では立体図形、とくに切断の発展問題が非常によく出題される。Z会『頻出分野別演習』立体図形難問対策では、切断を含めたさまざまな立体図形の難問を、難関校の入試問題なども紹介しながら扱っているので、開成の立体図形対策としてぜひ取り組んでみてほしい。
大問3の解説
大問3「切断した立体の展開図」は、立体の切断・展開図両方についての深い理解が必要な問題だった。立体図形の学習においてぜひおさえておきたい要素がつまっているので、解答に至るまでの理由をふくめ、しっかり確認しておこう。
大問3の問題のダウンロードはこちら (463KB)
(1)面②、面③、面④
(2)~(4)以下解説に記載
(5)1.8㎠
(1)解説
見取図と展開図の両方に点A、B、Cが記載されているので、立体Yの展開図の面②は、直方体Xの見取図の以下の面上にあるとわかる。
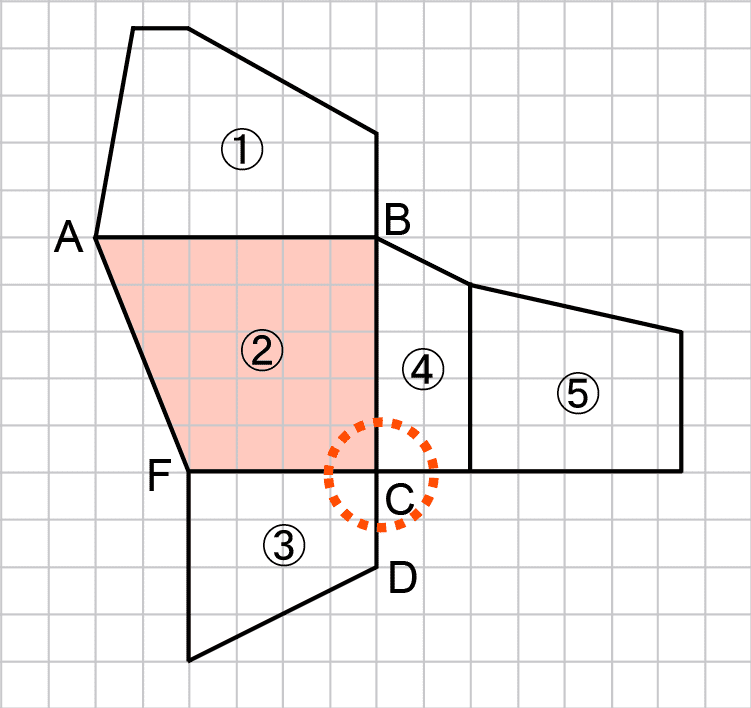
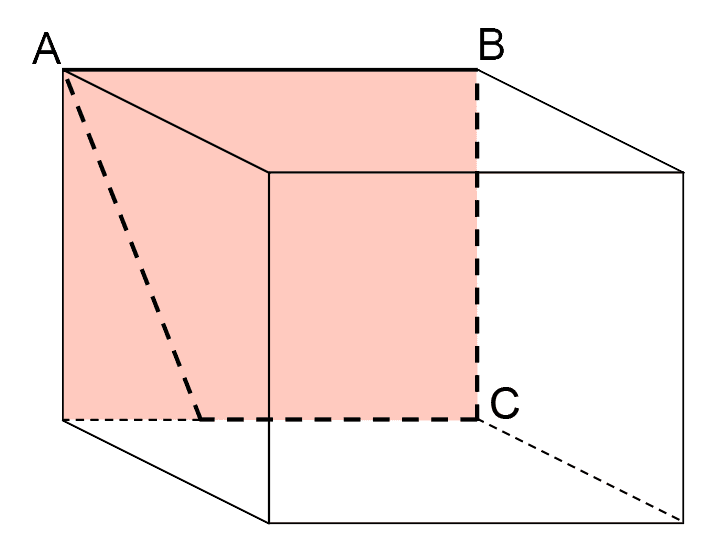
立体図形のポイント1
(一直線上にない)3点を選ぶと平面は1通りに決まる。
つまり、面②は(1)の答えにあてはまる。
次に注目するのは、展開図の点Cに集まった面である。面②・③・④はどれも点Cにあたるところが直角のため、組み立てたときの辺CDは面②に対して垂直に交わっている。
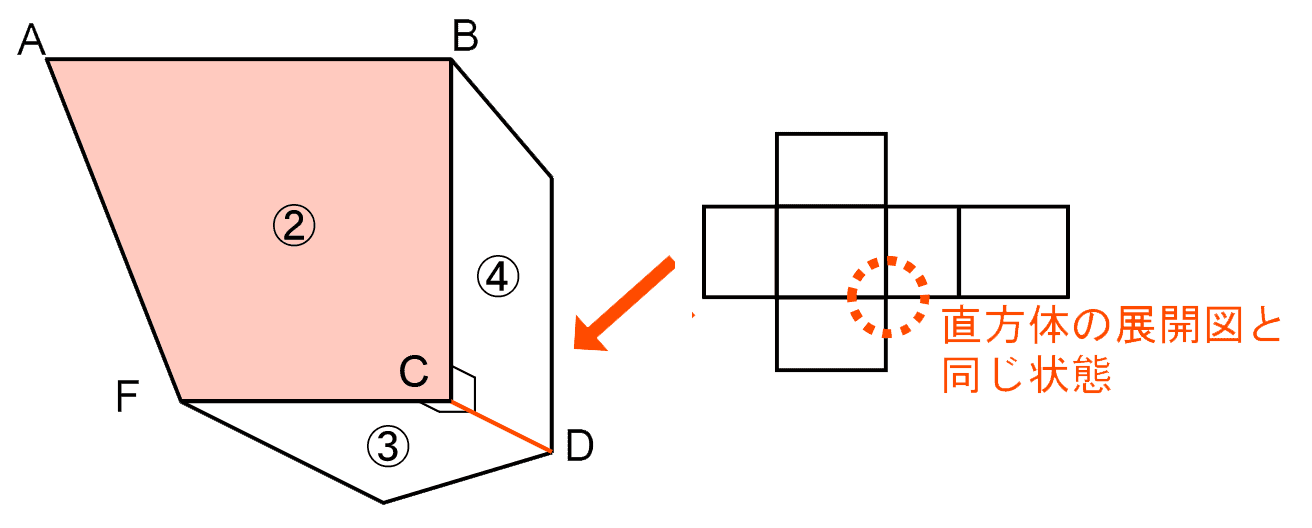
立体図形のポイント2
辺CDは、面②上の辺BC・辺CF両方と垂直なので、辺CDと面②は垂直。
したがって、辺CDは直方体Xの辺の一部となっている。そのため下の図のように考えることができ、面③・④は(1)の答えにあてはまり、面①・⑤は(1)の答えにあてはまらないとわかる。
(面①・⑤は、面④や面③の、方眼に対してななめの辺に接しているため、判別しやすいだろう。)
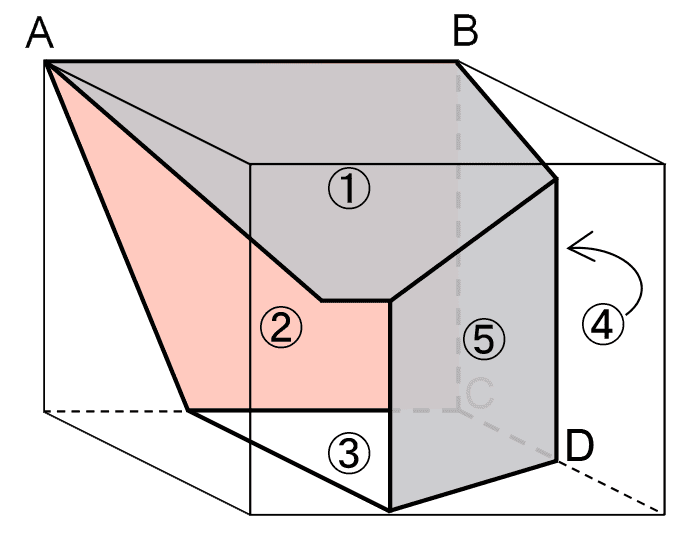
(2)解説
(2)で点D、Fに加えて点Eも辺上にあることがわかる。
まずわかりやすいのが面②の点Fだろう。辺ABは直方体Xの辺であり、長さが方眼6マス。辺CFは4マスのため、点Fは直方体Xの横の辺を、(6-4):4=1:2に分ける位置にある。
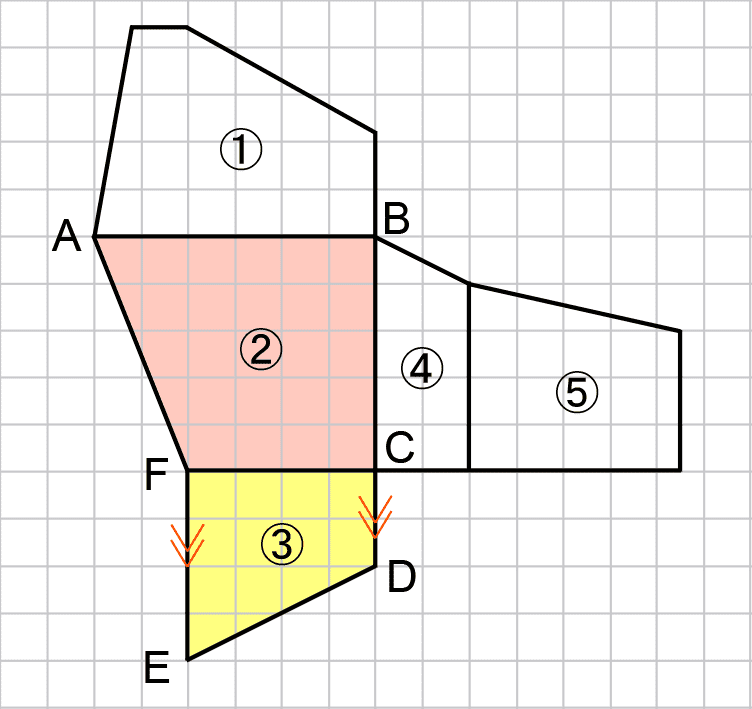
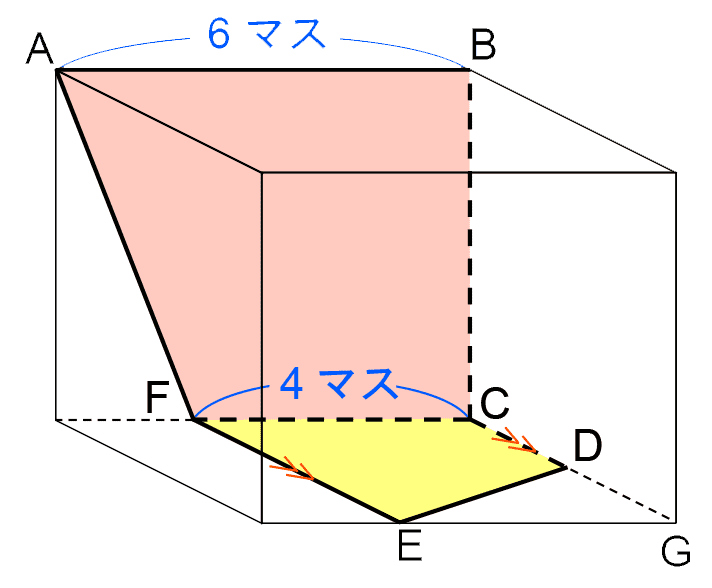
次に、面③に注目する。面③は辺CDと辺FEが平行な台形である。辺CDは直方体Xの縦の辺の一部であるため、それに平行な辺FEは直方体Xの縦の辺と平行になっている。
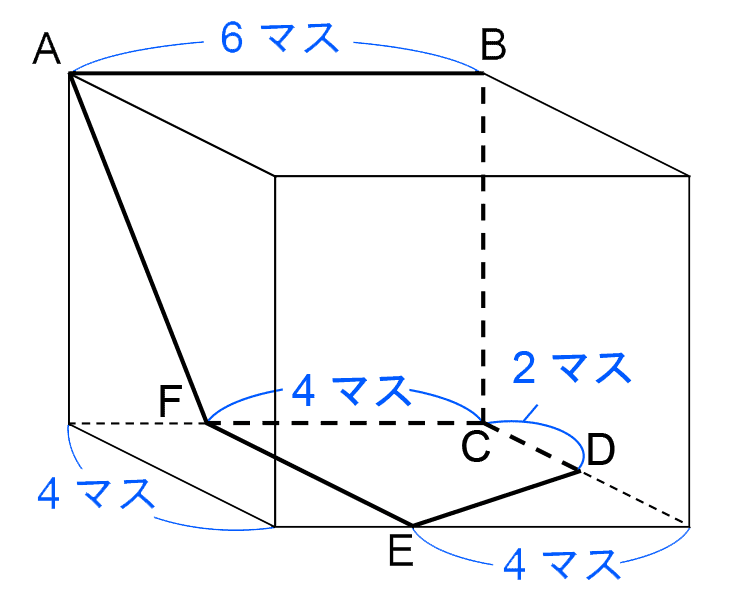
つまり、上の図のように点Gをとると、四角形FEGCは長方形(正確には正方形)だから、EGの長さはFCと同じで4マス、直方体Xの縦の長さはFEと同じで4マスとわかる。
立体図形のポイント3
平行な線はヒントになることが多い。
以上より、点Eは直方体Xの横の辺を1:2に分ける位置、点DはCDの長さが2マスだから、縦の辺のまん中の位置にある。
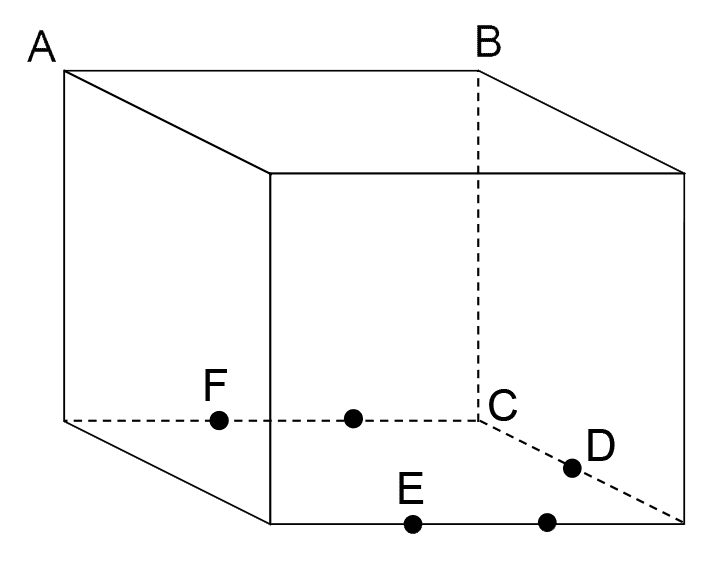
(3)解説
点D、E、Fの位置が(2)でわかったので、いよいよ3回の切断がどのように起こったかを調べていく。
まず、直方体Xのどの辺りを切断したかをざっくりと考えると、面②の辺AF、面③の辺DE、面④の方眼をななめに通る辺は、切断によってできている辺である。面①~⑤を組み立てたようすを想像すると、これらは1つの平面による切断では同時に起こらないので、この3つが3回の切断にあたると推測できる。
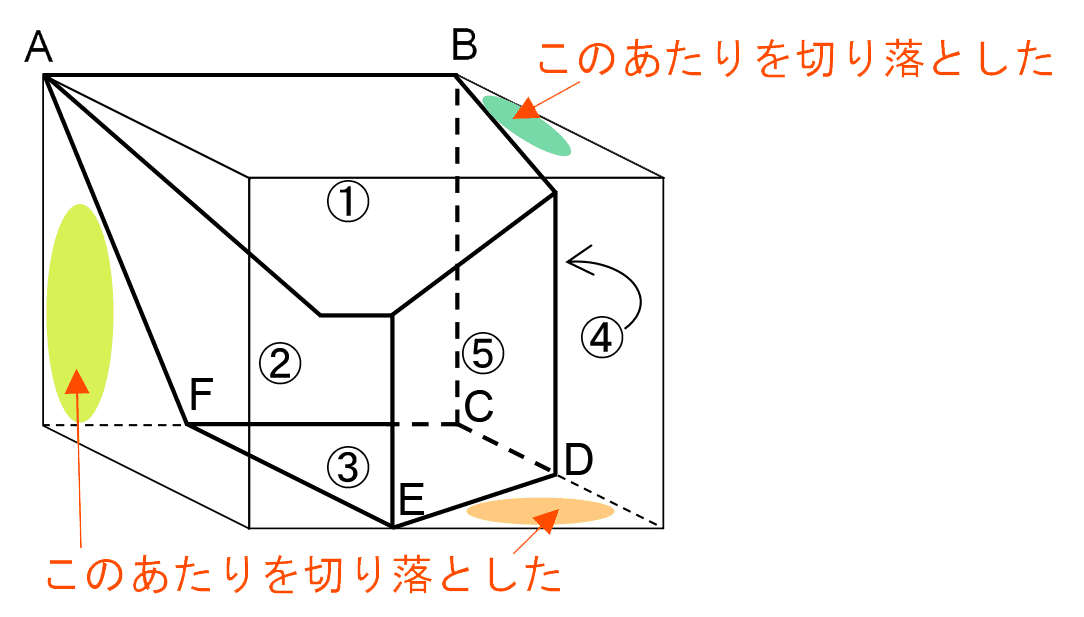
ここからは1つ1つの断面を考えていく。
まず、面②の辺AFをふくむ断面は、3点A、F、Eを通る平面である。
直方体Xの向かい合った面は平行で、FEは縦の辺に平行なため、断面は以下のようになる。
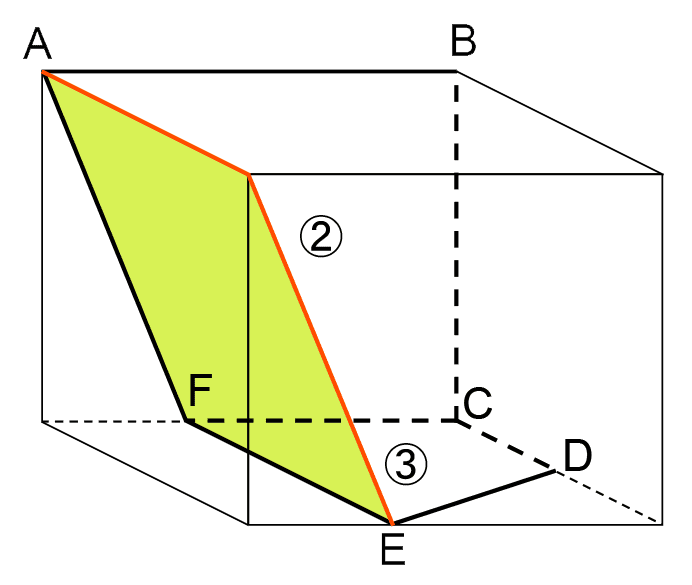
立体図形のポイント4
平行な2つの面に1つの平面(切断面)が交わるとき、交わってできた2本の直線(交線)は平行になる。
次に、面③の辺DEをふくむ断面を考える。この切断によってできる面が面⑤にあたるが、展開図より面⑤の辺は辺BCと平行になっているので、断面は以下の図のようになるとわかる。
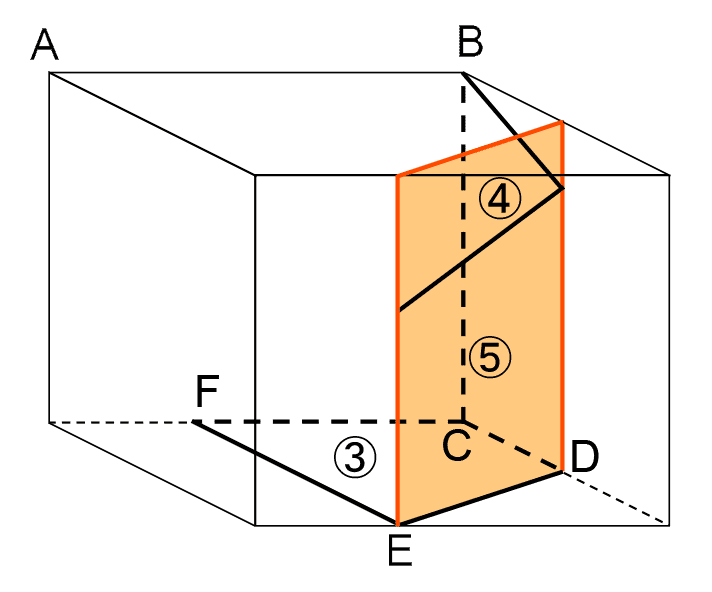
最後に、面④のななめの辺をふくむ断面を考える。このままでは断面を考えにくいので、面④のななめの辺を延長して直方体Xの辺上とぶつかる点をHとすると、左下の図よりHGの長さは3マスである。
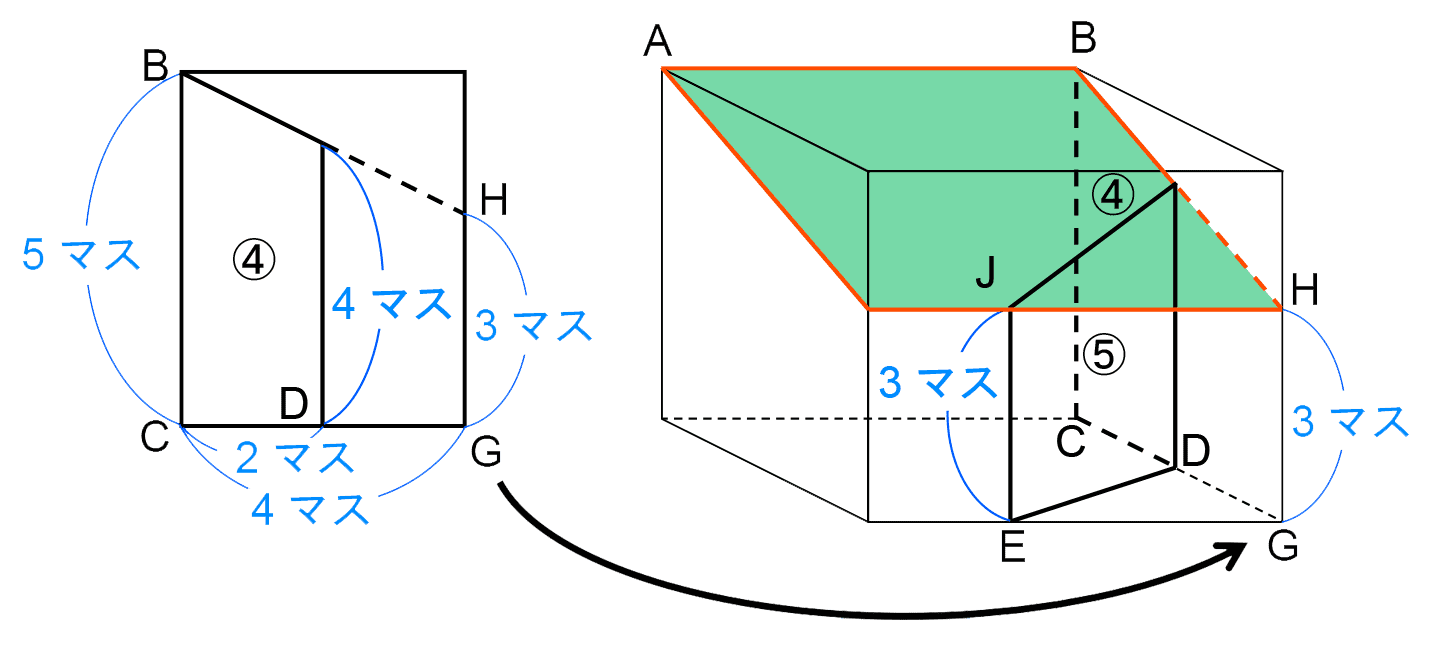
直方体Xの手前の面で見たとき、HGの長さは3マス、右上の図のJEの長さも展開図より3マスとわかるため、手前の面の切断線は直方体Xの横の辺と平行になり、断面は右上のようになるとわかる。
したがって、3種類の断面は以下のようになる。
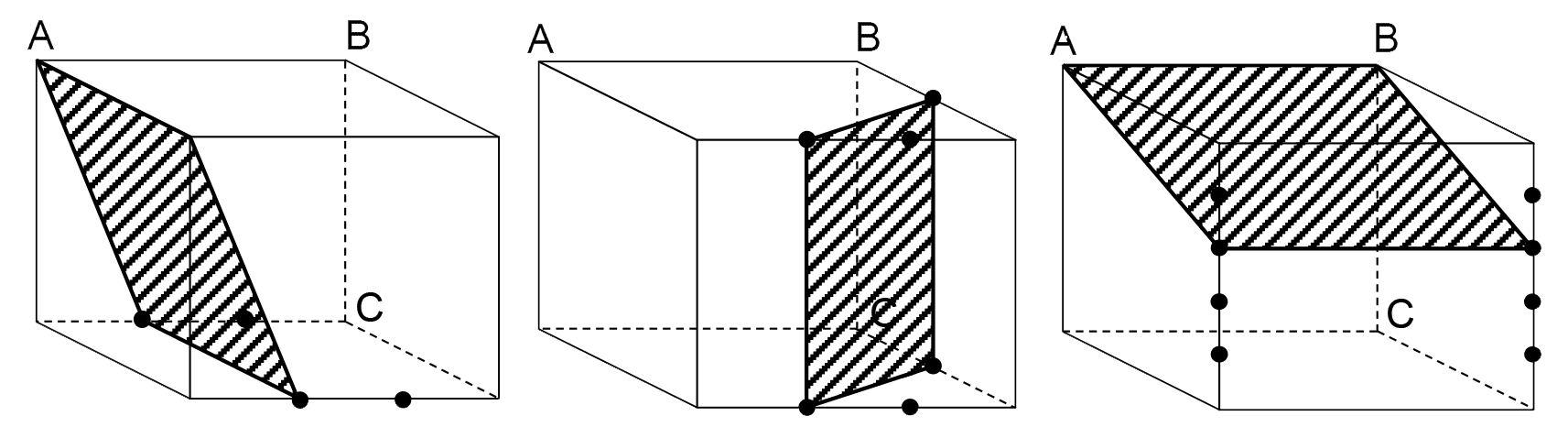
(4)、(5)解説
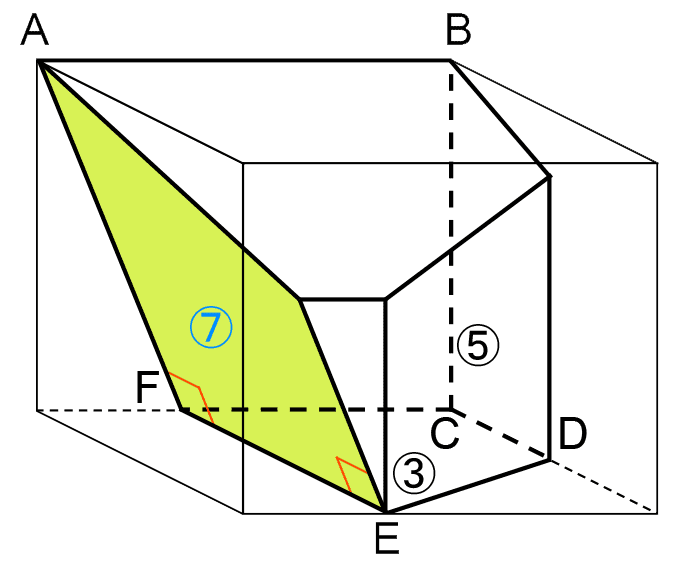
(3)で3回の切断のようすがわかったので、立体Yが左下のような立体だとわかる。
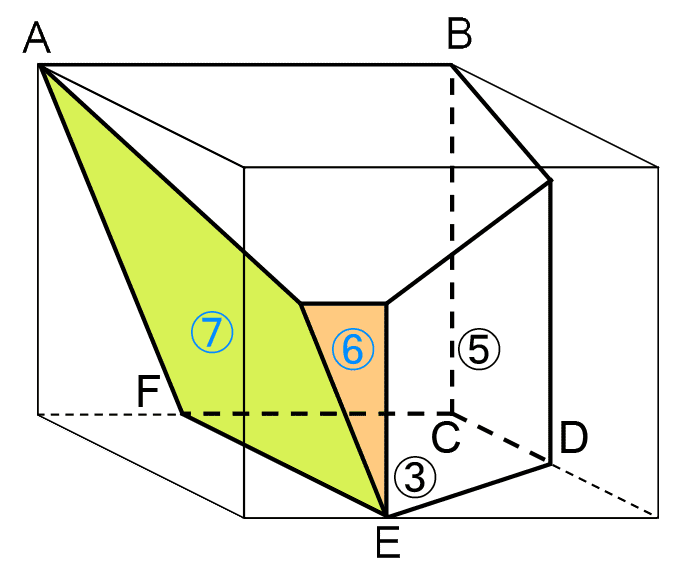
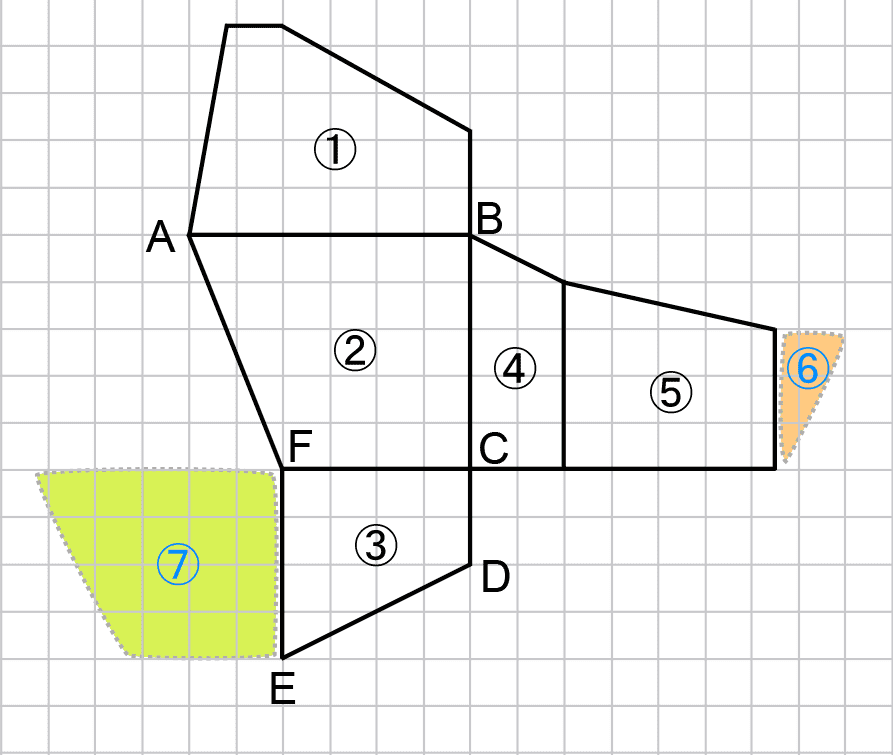
展開図の残り2つの面が左上の面⑥、面⑦にあたるため、展開図はだいたい右上のような形になるとわかる。
ここから、なるべく正確にかくために面⑥と面⑦のようすを調べていく。
まず、面⑥は直方体Xの面を手前から見たとき、以下のような図形となっている。
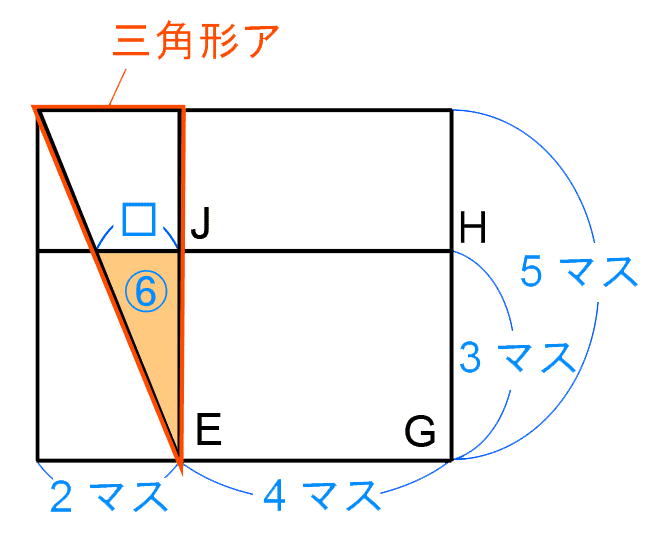
立体図形のポイント5
断面の辺の長さを知りたいときは、考えやすい面(または平面)上で相似を見つけることが多い。
上の図のHJは直方体Xの横の辺と平行であり、JEは直方体Xの横の辺と垂直であるため、HJとJEは垂直に交わる。
したがって、面⑥の三角形は直角三角形であり、三角形アと相似になっている。
面⑥の三角形と三角形アの相似比は3:5だから、□の長さは、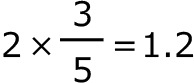 (マス)。
(マス)。
(5)ではひと目盛を1cmとするため、面⑥の面積は、1.2×3÷2=1.8(㎠)と求められる。
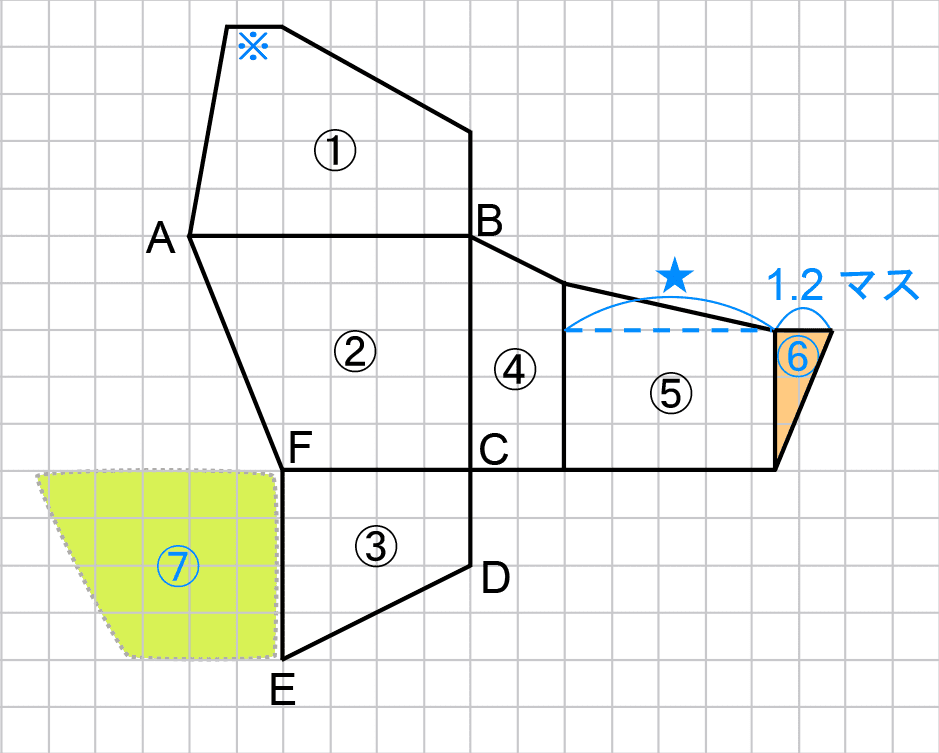
直角三角形の各頂点は方眼の格子点を通らない。面①の※の辺の長さをコンパスではかりとるか、もしくは上の図の★の長さがだいたい4.5マスぐらい(この長さは小学生では正確に表すことはできない)だから、そこからさらに1.2マスぐらいのばしたところで辺をとればよいだろう。
次に面⑦を見ていく。面⑦の辺FEは直方体Xの前後の面と垂直だから、面⑦は直角を2つもつ台形である。
立体図形のポイント6
面と辺が垂直のとき、面の中の直線と辺が交わる場合は必ず垂直に交わる。
したがって、展開図は以下のようになる。展開図を組み立てたときの重なりから、以下の図の同じ記号の辺の長さが等しくなることに注意する。
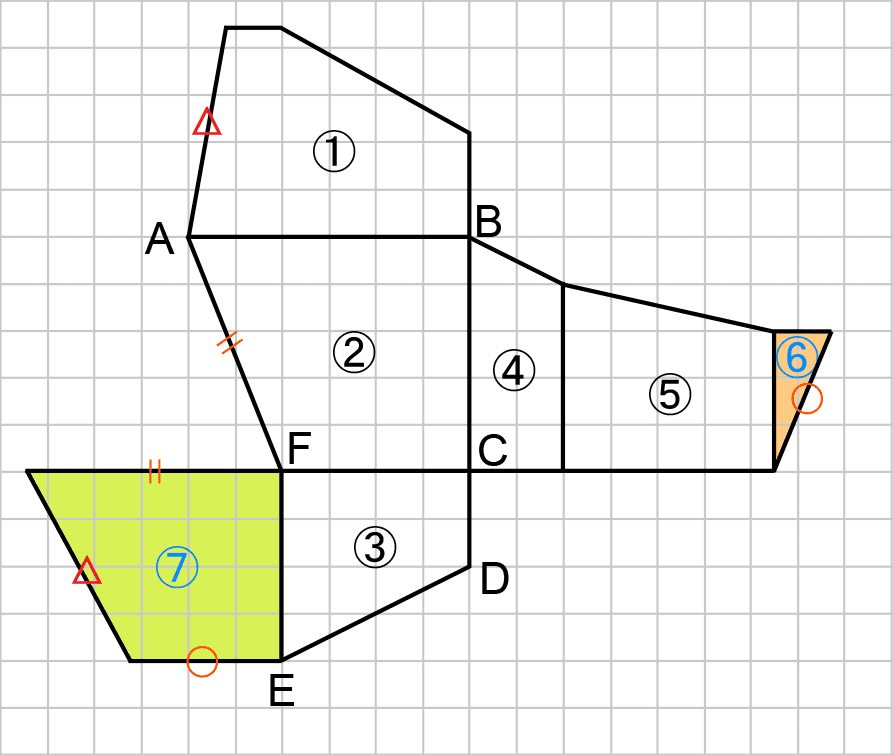
以上より、(4)の答えは以下のようになる。
【開成対策に!】Z会の専科講座【算数】
3か月完成(毎月1回のお届け)の「Z会中学受験コース 専科」。塾での学習と並行しても負担の少ない教材量で添削指導までついており、通塾の方にもプラスオン教材としておすすめです。
「頻出分野別演習」の他にも、開成中学を想定した予想問題をお届けする専科「志望校別予想演習」、超難問群に取り組む「最難関中学受験プレミアム講座」などもございます。今の学習状況・やりたいことに合わせてご受講ください。
「Z会 筑駒・開成受験応援LINE」のご案内

