差がつく一問(2019)_第2弾（京大文系数学編）

2019年度の合否を分けた「差がつく一問」は？

Ｚ会では、2019年度の受験生の答案を独自分析。合格者と不合格者の答案を比較し、「どの大問の出来が合否を分けたのか」を検証しました。それにより導き出された「差がつく一問」は…？

⇩

差がつく一問は、

≪第２問≫

実際の答案＆添削を見ながら、差がつくポイントを確認しよう！

以下の答案は、実際に入試を受験したＺ会員の先輩がつくってくれた再現答案です。目標点（合格ライン）には達していません…。
まずは、実際の答案をＺ会の添削指導付きで見てみましょう。そのうえで、Ｚ会の分析を読み、どこで差がついたのかを確認していきましょう。

目標点とのギャップをどう埋める？

xの符号で場合分けして絶対値を外すこと、bが文字定数であることを見定めて、aとbの大小関係で場合分けという方針は理解できていますね。
〔1〕、〔2〕の場合分けによる最小値の考察までに25点分の配点があるのですが、ここから―10点の減点になっています。減点理由は「関数ｆ(x)の定義域全体で最小値を考えていないこと」です。

たとえば、〔1〕(i)の場合、a≧bのとき

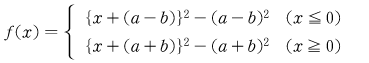
について、2つの放射線の軸 x＝―(a―b)とx＝―(a＋b)の位置関係を考えると、b＞０より

０≧―a＋b＞―a―b

ですから、この場合のｙ＝ｆ(x)の概形は以下の図のようになります。
結果的に最小値は―(a―b)²にはなりますが、このような考察過程を記しておかなくてはいけません。

受験生全体の解答傾向

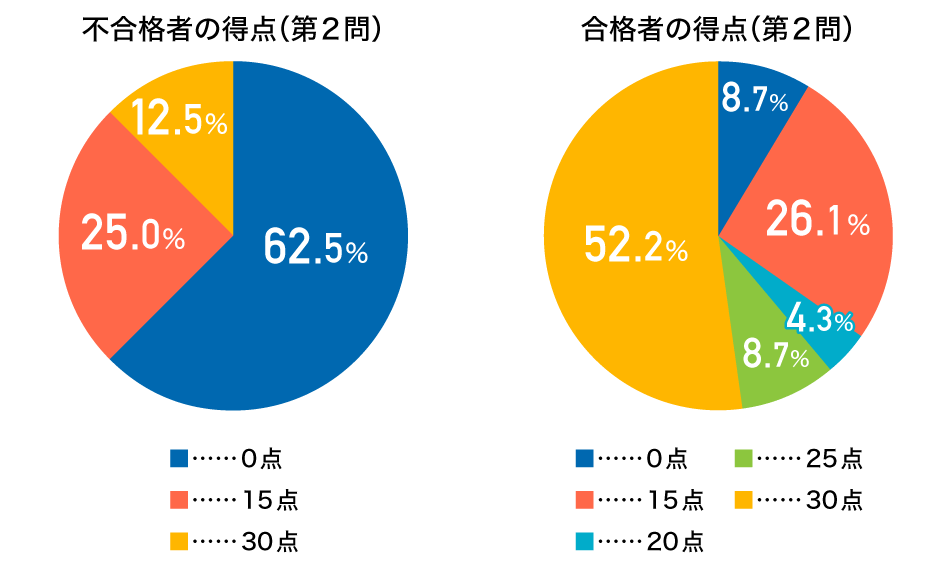
グラフに示したとおり、不合格者の大半は15点以下で、合格者の大半は15点以上となっています。つまり、この問題の不合格者と合格者の得点差は非常に大きいということです。
さらに、不合格者と合格者の総得点の平均も、不合格者は39.6点、合格者は84.7点で約35点もの大差が開いており、文系の大問1問分より多いことになります。「文系だから数学はできなくても仕方ない」は通用しません。むしろ、この差を他科目で挽回することの方が難しく、「文系だからこそ数学をしっかり勉強しなくてはいけない」という現況をしっかり認識して、対策を立てなければいけません。

Ｚ会でできる京大対策・ご案内

ほかの科目の「差がつく一問」を見る