Ｚ会の大学受験担当者が、2022年度前期試験を徹底分析。長年の入試分析から得られた知見もふまえて、今年の傾向と来年に向けた対策を解説します。

今年度の入試を概観しよう

分量と難度の変化

• 難易度はやや難化
• 分量は昨年並み

2022年度入試の特記事項

• 理系としては5年ぶりに確率が出題された。なお、東大の確率で一時頻出した確率漸化式ではなく、近年文系も含めてよく見る、漸化式ではないタイプである。
• 整数や立体といった東大で頻出の分野からの出題もあり、適度に難易度差もついた東大らしいセットであった。
  

合否の分かれ目はここだ！

• 大問ごとの難易度には適度に差がついているのが通例である。また、難しい大問では、(1)として手のつけやすい設問が設けられていることが多く、前半の(1)で導いたことをどのように後半につなげるかがポイントとなる。易しい大問や、難しい大問の前半で確実に得点を重ね、後半でも部分点を確保して、全体で5割前後は得点したいところである。
• 本年度では、第１問、第３問を押さえた上で、離散系が得意な人なら第２問・第６問から、微積分が得意な人なら第４問・第５問から、いずれか１問分以上押さえていれば十分であろう。

さらに詳しく見てみよう

大問別のポイント

　第１問　　

• 数学Ⅲの微積分の計算問題。難しくはなく、必ず押さえておきたい問題であった。
• (1)では、「微分と積分の関係」や三角関数絡みの符号の評価が問われたが、易しい。
• (2)は、置換積分や部分積分といった工夫を要するが、東大で頻出の形でもあり、東大受験生であれば演習の中で経験していたレベルであろう。怖いのは計算ミスであり、焦らず着実に進めたい。
  

　第２問　　

• 整数問題。漸化式から数列の構造を捉えることが問われていた。
• (1)は、定石どおり5で割った余りの周期性を指摘すれば直ちに示せる。論証の形式としては、数学的帰納法でまとめるのが簡明だろう。
• (2)が難しい。(1)の結果あるいは過程からヒントを得ていきたい。いろいろなアプローチがあり得るが、(1)で示したのが「nが3の倍数であることは、a_nがa₃の倍数であるための十分条件」であったと気づくと早いだろう。ただし、答えの見当がついても、必要性の証明は整数問題のセンスを身につけていないと書きにくい。
• (3)では、8091=2022×4+3に注目して、最大公約数のわかる形に整理していく。(2)ができた人は、ここでも得点を上積みしたい。
  

　第３問　

• 放物線や領域を題材とした問題。わかってしまえば考察も計算も全く難しくはないが、「適切な図がかけるか、状況が理解できるかで差がつく」というタイプであった（東大ではこういったタイプの問題は少なくない）。とはいえ、合格のためにはこれも落とせない。
• (1)は状況把握の第一歩であり、確実に取りたいところだが、実際には混乱してしまった人もいるだろう。下の図のような図がかけていればOKである（大きな正方形がDであり、灰色の部分が(ii)によって除かれる部分）。　

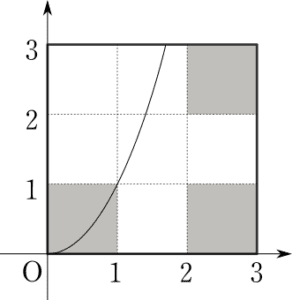
• (2)では、さらに点P(a, a²）を中心とした面積4の正方形を図にかき込むことになる。位置関係により場合分けが生じるが、しっかり図がかけていれば難しくはない。そのあとの(3)も易しい微分法である。

　第４問　

• 微分法で、3次関数のグラフを扱う問題。数学Ⅲの微分法をもち出す必要はなく、内容的には文系数学の範囲である。正しく議論を進めれば処理も考察も大変ではないが、実際には迷路に迷い込んでしまった人も多そうだ。
• (1)では、「f(x)=0が3つの実数解をもつ⇔f(x)の極値の積が負」のような3次関数の扱いが問われた。(2)では、「直線lは曲線Cの対称の中心を通る」ことがポイントであった。いずれも、数学Ⅱの微分法を集中的に演習している文系の受験生ならお馴染みの発想だが、理系では使える道具も多く、また数学Ⅲを中心に演習していることから盲点になりやすいところである。
• とはいえ、微積分を得点源とする人なら、少なくとも途中までは取っておきたいところだ。

　第5問　

• 空間図形の問題で、断面を考えて体積を求めるというもの。東大ではよく問われているテーマである。闇雲にではなく、構想をもって見通しよく進めたい。
• 本問の立体は回転体であり（あるいは、回転体と判断できなかったとしても、少なくとも対称性から）、z軸に沿った積分で体積を求める方針が立つだろう。そうすれば、当面の最大の目標として、z軸に垂直な断面の面積を求めることを目指せばよいとなる。
• Mのz座標を決めると、Pのz座標が決まる。Pを固定するとMの軌跡は円なので、それが動いてできる領域の面積を立式するのは困難ではないだろう。ただし、場合分けには注意が必要である。自分のかいた図から先入観をもたないようにしたい。
• そのあとの積分計算は、定番の処理であり第１問よりも易しいが、面倒である。順調に進めばよいが、計算ミスなどで泥沼になってしまった場合は、いったん他の問題に移るのも実戦的である。難問ではないが、解き切ることを考えると決して易しくはない。
  

　第6問　

• 確率の問題。Nのような文字を含んだ確率の問題では、「状態遷移を考えて漸化式を立式する」という方針もあり得るが、本問では状態の個数が多くなりすぎてうまくない。もう一つの有力な方針は、漸化式ではなく、順列Pや組合せCなどを使って直接立式するというものであり、本問もそれが適するタイプであった。
• ランダムウォークとみると、点が進む方向が「今までに裏が出た回数」によって決まるランダムウォークである。つまり、コインの裏が出るごとに点の進む方向が変わるわけであり、そう考えると、「進む方向（＝裏が出た回数を3で割った余り）ごとに表の回数を数える」という発想にも至りやすかったかもしれない。
• 本問のベクトルは、複素数平面でいえば1、ω、ω²（1の3乗根）に他ならない。複素数平面として見ると、「a+bω+cω²=0が成り立つとき、a=b=cである」という本問のポイントにも気づきやすかったかもしれない。本年度は複素数平面の出題がなかったが、間接的に複素数平面のセンスが問われていたともいえそうだ。

 攻略のためのアドバイス

東大理系数学を攻略するには、次の３つの要素を満たす必要がある。

●要求１● 高度な思考力

特別な知識は要求されないものの、高いレベルの思考力、発想力を試す問題が多く出題されている。他の大学では、一見しただけで典型問題だとわかる出題が多いが、東大では出題の仕方がかなり工夫されており、すぐには問題の解法が浮かびにくいものが多い。初見の問題に色々な面からアプローチして、解法を決める力が求められる。確率、整数の問題で主にこの力が問われる。

●要求２● 早く正確な処理力

例年、処理量の多い問題が出題され、比較的処理量の少ないものでも、1問あたり20～30分くらいかかるものもある。特に積分の求積問題で、ハードな計算を要求するものが多い。また、やや高度な出題も見られるが、処理力重視の問題は、方針が立てやすい。数式処理力の差は直接得点差につながりやすいので、速く正確に処理できる力を充実させておきたい。

●要求３●解ける問題を見極める力

東大の数学では、例年、5割程度取れれば合格ラインといえる量とレベルの出題である。つまり、全問を解く必要はなく、解く問題の選択が合否を分ける。過去問演習などを通して、完答できる問題を見極める力を養っておこう。小問ごとに解ける問題は、もちろん解くべきである。

対策の進め方

まずは、苦手分野があれば、遅くとも受験生の夏休みまでには克服したい。ただし、基本的なことばかりやっていては、高度な思考力を要求される東大入試には太刀打ちできなくなる。
受験生の秋以降は実戦的な演習を行い、得点力アップを図ろう。また、答案を作成する力の養成も意識したい。
共通テストが終わったあとは、東大入試に即応したＺ会の問題で、最後の総仕上げをしよう。解答を作成する時間や、採点者にきちんと内容の伝わる答案作りを意識し、実戦力を完成させよう。
Ｚ会の講座では、上記の各段階に応じて、東大対策を無理なくこなせる設計になっている。Ｚ会の講座を活用して、ライバルに差をつけよう！

Ｚ会で東大対策をしよう