Z会の東大コース担当者が、2022年度入試の東大理系数学を徹底分析。受験生の再現答案や得点開示データをもとに、合否を分けた「差がつく一問」を選定し、東大理系数学の攻略法を詳しく解説します。
まずは、2022年度の「東大理系数学」を俯瞰しよう
はじめに、問題構成や出題傾向をおさえて、「自分が受ける入試問題」を正確に把握しましょう。
解きやすい問題の見極めが重要
今年度も例年と同様に、難易度が高い問題の合格者・不合格者の平均点はともに低めでその差は小さいですが、解きやすい問題の合格者・不合格者の平均点の差が大きいようです。この差が合否に大きく影響しているといえます。
合否の分かれ目は?
合格者・不合格者の平均で最も大きく差がついた大問が第3問であり、抽出した答案では7点以上の差がありました。この他、第4問も差が大きく5点以上の差がありました。これら以外の大問では、第2、5、6問の難易度が高く、各大問で部分点をどのくらい得点できるかポイントになったようです。第1問を完答し、第2、5、6問でどの程度、得点を積み増すことができるかによって、さらに合格者と不合格者の差がついたと思われます。
⇩
差がつく一問は
≪第3問≫
差がつく一問の注目ポイント
問題文中で述べられている「点Sが点Tから十分離れている」の理解、これに尽きます。東大では、本問のように問題の中で数式や言葉を定義し、それを用いて考察していく問題がときどき出題されます。問題文の中で定義されるのですから、当然、問題文は長くなりますし、予備知識は全受験生等しく0ですから、まさしく総合的な数学力が試される問題といえます。
(1)では「十分離れている」の意味の理解、(2)ではその意味を踏まえた場合分けの気づきがポイントであり、ここまでできれば(3)は自ずと得点できるでしょう。
受験生の再現答案&添削を見ながら、差がつくポイントを確認しよう
Z会では、受験生が作成したこの大問の再現答案を、独自の採点基準に基づいて添削しました!
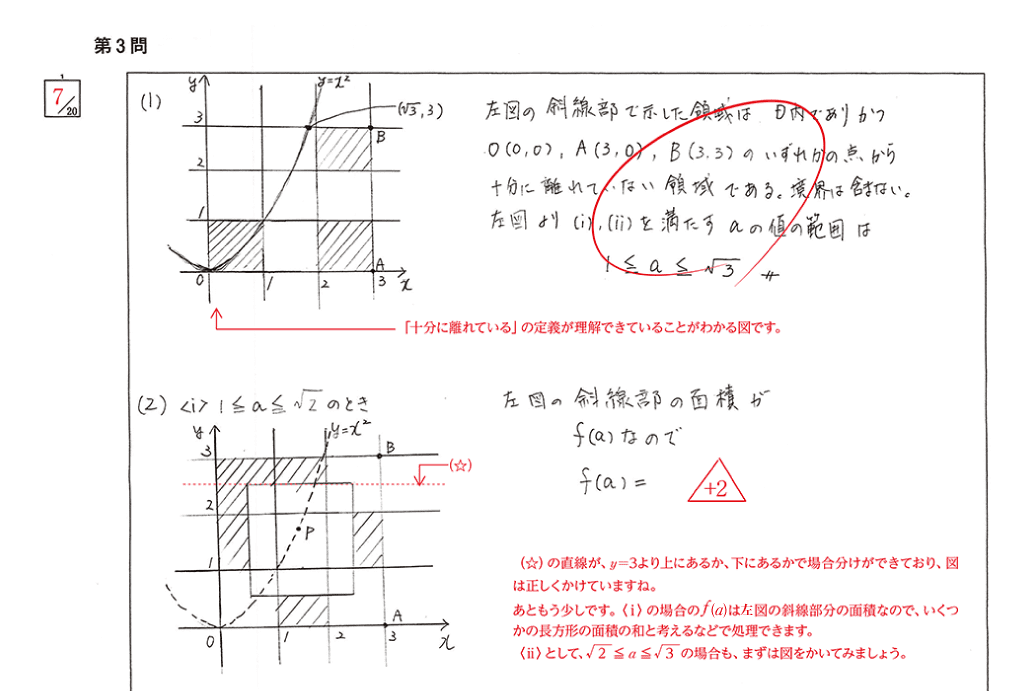
Z会が採点した結果は、Z会が設定した目標点である16点に対し7点となりました。

それでは、この答案には、「どんな要素が足りなかったのか」「どういう対策をしていれば目標点に届いたのか」を詳しく見ていきましょう。
目標点とのギャップをどう埋める?
図が主体の答案であり、説明不足と思う人も多いかもしれませんが、(1)や(2)の図をみるだけで、「十分離れている」ことが正しく理解できていると伝わってきます。他の大問構成を考えると、本問は論証重視ではなく、発想重視の問題であることが伺えるので、少なくとも(1)では、この答案の説明で充分と思われます。また、(2)は場合分けに気づいており、図も正しくかけているので、時間切れになったのではないかと推測しています。
もっと早く本問が比較的得点しやすい問題であることが見抜ければ、取り組む順番を変更することによって、おそらく満点近く得点できたのではないでしょうか。
受験生全体の解答傾向は?
不合格者では、白紙やそれに近いものもありますが、(1)はできていて(2)以降が白紙の答案が多いです。そして、そのような答案では、「図がなく、数式だけで処理」しようとしているものが目立ちました。(2)において手が止まってしまう大きな原因は、複雑な状況を把握しきれていないことです。図はこれを解決する手段の一つですので、積極的に活用してもらいたいです。
もちろん、図が万能であり、いつでも図をかけばよい、というわけではありません。数学では、図と数式をうまく組み合わせることが大切となります。互いの苦手なところを補完し合うように、適材適所で図と数式を使い分ける、このような思考を意識しながら演習していくとよいでしょう。
Z会が独自作成。この大問の採点基準はこちら!
大学から採点基準が公表されていない中、Z会では、実際の受験生の再現答案や得点開示データを毎年収集し、綿密に分析。長年の分析に基づいて作成した独自の「採点基準」で、本番に限りなく近い採点を可能にしています。
「2022年度入試 東大理系数学 第3問」の採点基準
配点 20点
(1)5点、(2)10点、(3)5点
(1)
□1 図や説明に2点
□2 正しいaの値の範囲に3点
(2)
□1 1≦a≦√2のときの考察に5点
□2 √2≦a≦√3のときの考察に5点
一言コメント:
(2)では、(1)の条件のもとで、「Pから十分離れている」という条件を加味して考えるとよいでしょう。採点としては、場合分けの可否が最大のポイントになります。
Z会の『過去問添削』で、東大対策を進めよう!

Z会では、特別講座『過去問添削』を開講中です。長年の分析に基づく正確な採点で現在の実力を正確に把握。そのうえで、あなたの答案に寄り添った適切なアドバイスにより、次の打ち手が明確になります。実戦力を効果的に高められる講座です。
Z会東大コース担当者からのメッセージ
東大理系数学の出題では、レベルの高い発想力、計算力、論述力が要求されます。しかし、すべての問題でこれら3つの能力すべてを要求しているとは限らず、大問によって受験生に問いたい資質能力を設定していることもあります。上記で取り上げた第3問は発想力に重きを置かれていますが、たとえば第1問では数式の処理力に重きを置かれています。
問題ごとに問いたい資質能力が違うのであれば、採点基準も重きの置き方が違います。計算力重視の問題における計算ミスは致命傷になりますが、発想力重視の問題における計算ミスは軽微な減点で済むなど、問題の主旨に合わせて添削基準が変わるわけです。
再現答案の分析結果とこれらのことを踏まえて、過去問添削の添削基準は作成されていますので、実際の入試の採点に近い採点を経験できるだけでなく、論述における不備などの添削指導を通して効率的に合格答案を作成するための力をつけることができます。

