更新日：2021年12月3日
執筆：中学受験コース教材開発者・Ｓ
「算数は嫌い…特に図形は苦手！」、そんな中学受験生のお子さまも多いのではないでしょうか。
そこで今回からは、Ｚ会中学受験コースで算数教材の作成を行っている担当者から、平面図形の問題で頻出の6パターンとその対策を前編・後編に分けてお届けします。
問題を解くときの着眼点や意識すべきポイントを知っておくだけでも、図形問題はとても解きやすくなります。今回紹介するものはすぐに使えるものばかりですので、ぜひ覚えてみてください。
前編では「多角形と角度」、「三角形の底辺比と面積比」、「平行四辺形上の相似」の３パターンについて取り上げます。
頻出パターン１
「多角形と角度」
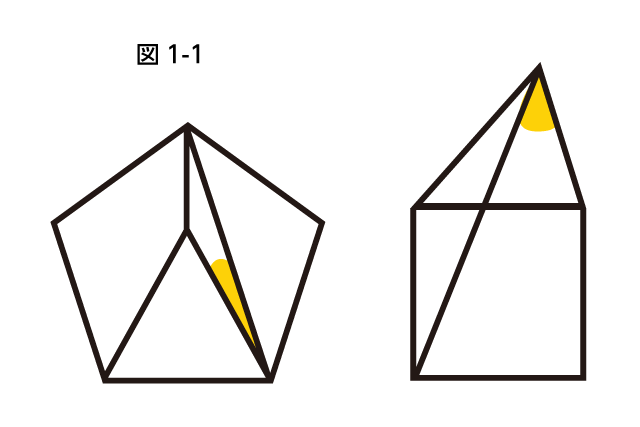
大問1や2などの小問集合で出題されやすいのが、多角形と角度の問題です。とくに図1-1で示しているような複数の多角形が組み合わさった形はよく出題されます。
対策法：「辺以外に引かれた直線」に注目する
多角形の内角や外角の大きさを求める公式は覚えているけれど、どのように考えを展開していけばいいのかわからないという場合は、求められそうな角度をとりあえず求めていく・図に書きこんでいく方法が有効です。
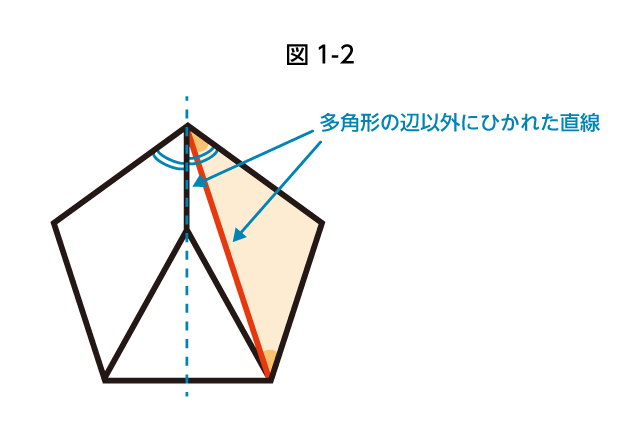
それでも詰まってしまった場合は、一度、問題の図を「まず正五角形があって，その中に正三角形が入っていて…」というふうにその成り立ちを確認しながらノートにかき写してみましょう。そのときに「多角形の辺以外に引かれた直線」が「どことどこを結んでいるのか」、「この線が関係する三角形や図形はないか」を考えてみましょう。次に角度がわかりそうなところを発見できるかもしれませんよ。
↓
2. 辺以外の直線に注目する
↓
3. その線が関係する三角形や図形がないかを確認する
頻出パターン2
「三角形の底辺比と面積比」
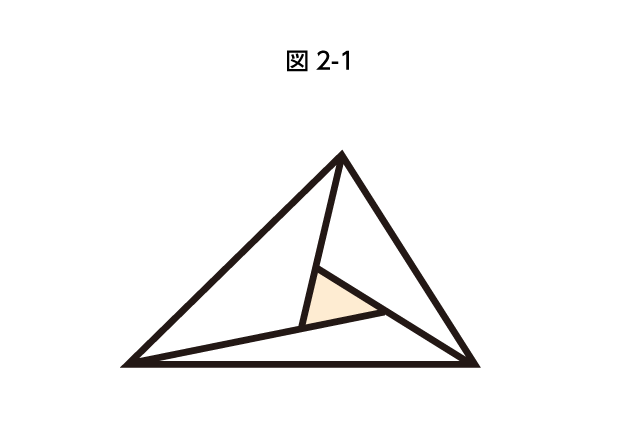
辺の長さの比や面積比を求める問題は、中学入試算数で多数出題されます。出題のされ方はいろいろですが、その代表といえば、図2-1のような図で真ん中の三角形の面積が全体の面積の何倍か、などを問うものでしょう。
対策法：「相似でない場合と相似の場合の面積比」に注意する
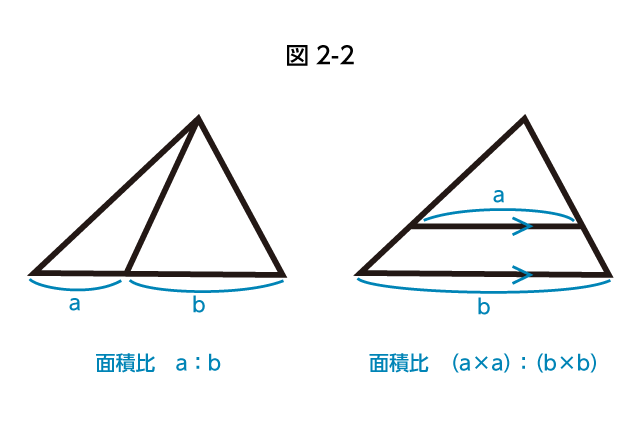
面積比といっても、図2-2のように辺の比と面積比が一致する場合としない場合があります。
まずここの差異をきちんと区別できているかを確認しましょう。
なお、このパターンの問題は、次に紹介する頻出パターン３「平行四辺形上の相似」とともに、今回取り上げた図がほぼそのまま出ることがありますので、補助線の引き方を含めて、考え方・処理の仕方を覚えてしまいましょう。ここで補助線の引き方を「なんとなく」でも身につけておけば、ややパターンの違う問題についても解きやすくなりますよ。
頻出パターン3
「平行四辺形上の相似」
「平行四辺形を使った相似」の問題も、中学入試では多く出題されます。図3のような問題では、左の図形は補助線がなくても相似が2種類見られるのでそれを手がかりに解いていくことができますが、右の図形は補助線を引いて相似を作り出すのが一般的な解法となります。
対策法：比の考え方を復習する
問題が図内の面積まで考慮する問題ならば、頻出パターン２と同様、底辺比と面積比の関係について、相似でない場合と相似の場合で区別をつけることが必須です。補助線の引き方や処理の仕方をある程度覚えてしまうことも有用でしょう。
ただ、こういった問題をパターン化して身につけるには、まず比を正しく扱えることが前提条件になります。
例えば、以下のような図形問題を見かけることも多いのではないでしょうか。
Ｑ：一直線上の点A、B、C、DについてAB：BDとAC：CDがわかっているとき，AB:BC:CDの連比は？
Ｑ：2つの三角形の面積比とどちらかの面積がわかっているとき，他方の面積は？
Ｑ：2つの三角形の面積比と面積の合計がわかっているとき、それぞれの三角形の面積は？
これらの問題は，そもそも比の性質（連比・比例式・比例配分）を理解できていることが前提になります。
相似比・面積比の問題は、辺の長さも面積も実際の大きさではない（比だけで考えていく）場合があるので、比の文章題の補強にもなります。じっくり取り組んでパターンを身につけるようにしましょう。
↓
2. 問題演習でパターンに慣れる
前編はここまでです。次回の後編では「折り返しと角度」、「多角形の回転移動」、「円の移動」について取り上げます。
Ｚ会の中学合格実績、中学受験対応コース・講座のご紹介
公立一貫校受検をお考えの方に 公立中高一貫校適性検査5・6年生
最難関中学受験をお考えの方に ［Ｚ会×エクタス］最難関中学受験プレミアム講座4～6年生