更新日：2021年12月17日
執筆：中学受験コース教材開発者・Ｓ
Ｚ会中学受験コースで算数教材の作成を行っている担当者から、平面図形の問題で頻出の6パターンとその対策をお届けします。
「図形問題はどう対策したら良いのかわからない」など苦手意識をもつお子さまも多いのではないでしょうか。
そんな図形問題ですが、問題を解くときの着眼点や意識すべきポイントを知っておくだけでも、とても解きやすくなります。
後編となる今回は、「折り返しと角度」「多角形の回転移動」「円の移動」について取り上げます。
前編で紹介したものと同様に、今回紹介するものもすぐに使えるものばかりですので、ぜひ覚えてみてください。
（※前編はこちら：「多角形と角度」「三角形の底辺比と面積比」「平行四辺形上の相似」）
頻出パターン4
「折り返しと角度」
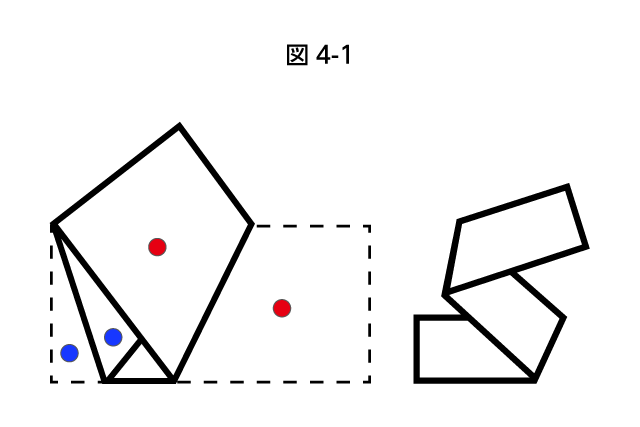
中学入試では、紙を折ったときの角度を考える問題もよく出題されます。長方形の紙を１回折る問題も出ますが、難易度が高くなるとテープのような長い長方形を数回折り返したものが出題されたりします（図4-1の右）。
対策法：1手戻した図をかく
紙を折る問題の最大のポイントは「折る前と折った後で合同な形ができる」ことです（図4-1の左、同色の丸が付いた図形は、折れ目を軸とする線対称）。
したがって、複雑に折られた図形の場合、折られる前がどんな形であったかを考えることが最重要になります。
まずは１手、折り返す前の状態をかいてみましょう。
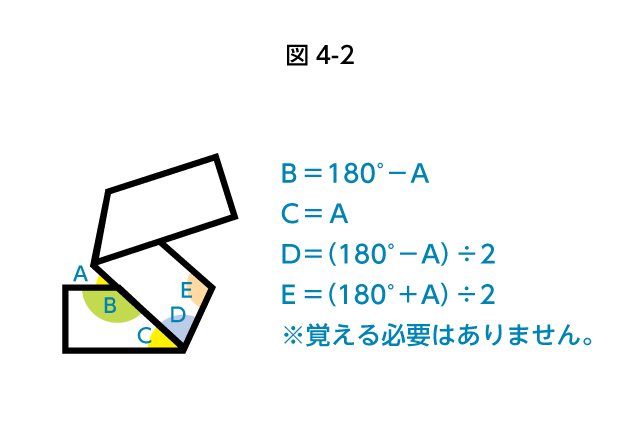
最後に折られた箇所を戻すか、最初に折られた箇所を戻すかは問題によります。基本的に対辺が平行なテープを折り返すとき、５つの角のうち、どれか１つが求まれば５つともすべて求めることができます（図4-2）。
折られる前の形を考える
折った前後では合同な形ができる
頻出パターン5
「多角形の回転移動」
多角形が直線上を回転移動していく問題は三角形や四角形を回転させることが多いです。
正多角形ではなく、直角三角形や長方形が回転する問題も少なくありません。
対策法：まず図形が回転するようすをかき出す
多くの問題では「点Aの動いた長さ」や「辺BCの通過した部分の面積」を問われますが、こういった問題で最初から点や辺だけに着目すると考えにくいですね。
まずは、どの点がどこに移動するかは考えず、図形の辺が直線に重なるごとの動きをかき出してみます（図5-2）。
図形が動くようすがかけたら、問われている点や辺の端点がどこに動くかを調べつつ、弧を記入していきます（図5-3）。
↓
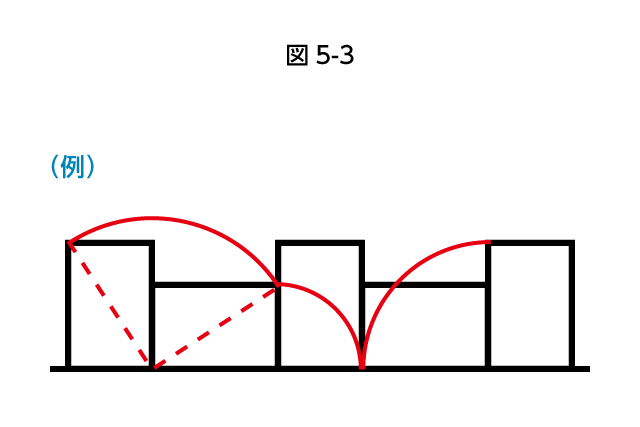
2. 点の動きを調べ、弧をかいていく
頻出パターン6
「円の移動」
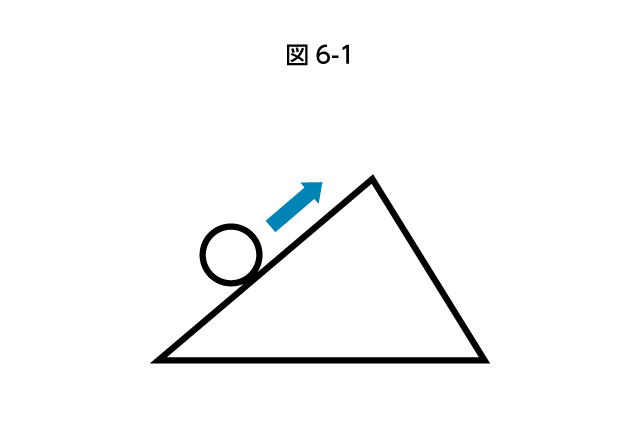
円が直線上や図形の辺上を移動していく問題もよく出題されます。中心の動きを聞かれることも円全体の通過面積を聞かれることもありますが、今回は円全体の通過の問題を取り上げます(基本的な考え方は同じです)。
対策法：直線移動と回転移動に分ける
円は直線上を進むときは中心も円全体もまっすぐ進みます。動きが変わるのは線が折れる箇所です。
したがって、まず横を辺、縦を円の直径とする長方形をすべての辺についてかき、次に長方形を結ぶように弧を描きます（図6-2）。
この弧は中心が線の折れた点にあたります。
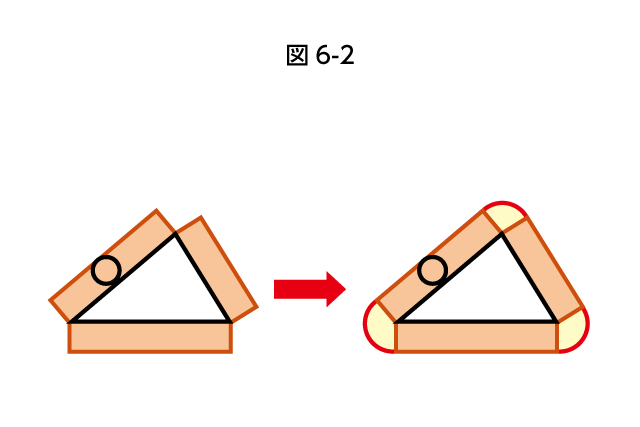
これで通過部分を図示できたので、あとは面積などを求めます（おうぎ形は半径の長さが円の直径にあたるので、その点に注意！）。
これが「円の動き」の基本です。折れ線が凹に折れている場合は複雑さが増しますが、円の移動の問題が苦手な人は、まずこの基本について図示がすっとできるようにしましょう。
※線が折れる箇所で切り替わる
↓
2. 面積を求める
直線移動部分（長方形） ＝（辺の長さ）Ｘ（円の直径）
回転移動部分（おうぎ形）※おうぎ形の半径は円の直径
いかがでしたか？全6パターンの解説は以上となります。
対策で何度も説明しましたが、平面図形分野の学習では「自分でかいてみる」「図示する」ことが欠かせません。
最初は時間がかかるかもしれませんが、問題の図形を自分の手でノートなどに改めてかき直すなどして、普段から図をかくことに抵抗がないようにしておきましょう。
慣れてきたら、ただ写すだけではなく、「今からかくのは正方形だ」「正三角形だ」「大体45度になるように角を描こう」など、かきながら問題の条件を意識するようにしていくと、だんだん図形の問題に慣れることができるはずです。
Ｚ会の中学受験コースでは、図形問題をはじめさまざまな単元を学習・習得できます。
中学受験対策に自分に合った問題をさらに解きたい方はご受講を是非ご検討ください！
Ｚ会の中学合格実績、中学受験対応コース・講座のご紹介
公立一貫校受検をお考えの方に 公立中高一貫校適性検査5・6年生
最難関中学受験をお考えの方に ［Ｚ会×エクタス］最難関中学受験プレミアム講座4～6年生