Ｚ会トップ > 先生・企業向け教育ソリューション > 教育ジャーナル > 共通テスト対策, 大学入試, 教材, 数学, 書籍 > 共通テスト数学　新課程入試に向けて　～試作問題の分析結果、新課程共通テストの出題予想～

共通テスト数学　新課程入試に向けて　～試作問題の分析結果、新課程共通テストの出題予想～

2024.05.30

Ｚ会ソリューションズ先生向け教育ジャーナル

Ｚ会ソリューションズでは、中学・高等学校の先生向けに教育情報を配信しています。大学入試情報、文部科学省の審議会情報をはじめ、先生方からお伺いした教育についてもご紹介します。

2025年度の共通テストは、新課程入試の1回目です。新しい分野も入り、過去問だけでは対策しきれません。そんな入試に向けた対策書籍を制作するにあたり、どのような分析をし、対策が必要と考えたのか、そして、対策書籍としてどんなものができあがったのかをご紹介します。

問題をどう作っているのか

我々が共通テスト対策書籍の問題を作成する際は、入試センターが共通テストでどのような問題を出題したいのかを考えて作成しています。どのような問題かは、次の大学入試センターのホームページ内にある「大学入学共通テスト問題作成方針」に記載されています。

https://www.dnc.ac.jp/kyotsu/shiken_jouhou/r7/

この中にある数学の問題作成方針では、以下のようなものが挙げられています。これらは、新課程で新たに方針となったのではなく、共通テストが開始されたときから変わりません。

数学の問題発⾒・解決の過程を重視する。
事象を数理的に捉え、数学の問題を⾒いだすこと、解決の⾒通しをもつこと、⽬的に応じて数、式、図、表、グラフなどの数学的な表現を⽤いて処理すること、および解決過程を振り返り、得られた結果を意味づけたり、活⽤したり、統合的・発展的に考察したりすることなどを求める。
例えば、社会や⽇常の中から課題を発⾒し解決⽅法を構想する場⾯、資料やデータ等をもとに考察する場⾯、考察したことを整理して表現しようとする場⾯などを設定することによって、探究的に学んだり協働的に課題に取り組んだりする過程を、問題作成に効果的に取り⼊れる。

毎年、共通テストが終わった後、追試も含め、すべての問題で、どの部分が作成方針に合致しているのか、どのような資質を問う問題であったかなどを分析し、次年度の共通テスト対策書籍の構成を検討します。その際、難易度や出題分野、単位問数などを振り返るだけでなく、数学ＩＡだけでなく、数学Ｉと共通な部分などをふまえ、本当はこんな問題にしたかったのではとか、どのような要素を含んだ問題であったかまで分析します。

このような分析をふまえ、問題を作成しています。作成方針の最後にある例えのような状況の問題も意識しており、学校現場でどのような学習を進めるのがよいと考えているかなどを検討し、それに沿った問題を作成することもしています。

これらの作成方法は、弊社書籍で扱った問題と本番の問題を比べて、間違っていないように感じております。例えば、2024年度の数学ＩＩＢでは、対数関数の領域の問題が出題されました。弊社書籍でも図１のように、同じテーマの問題を扱いました。また、2024年度の数学ＩＡの追試では、整数問題で７進法で表された数を入れ替えて考察する問題が出題されましたが、弊社書籍でも図２のように、同じテーマの問題を扱いました。

図１

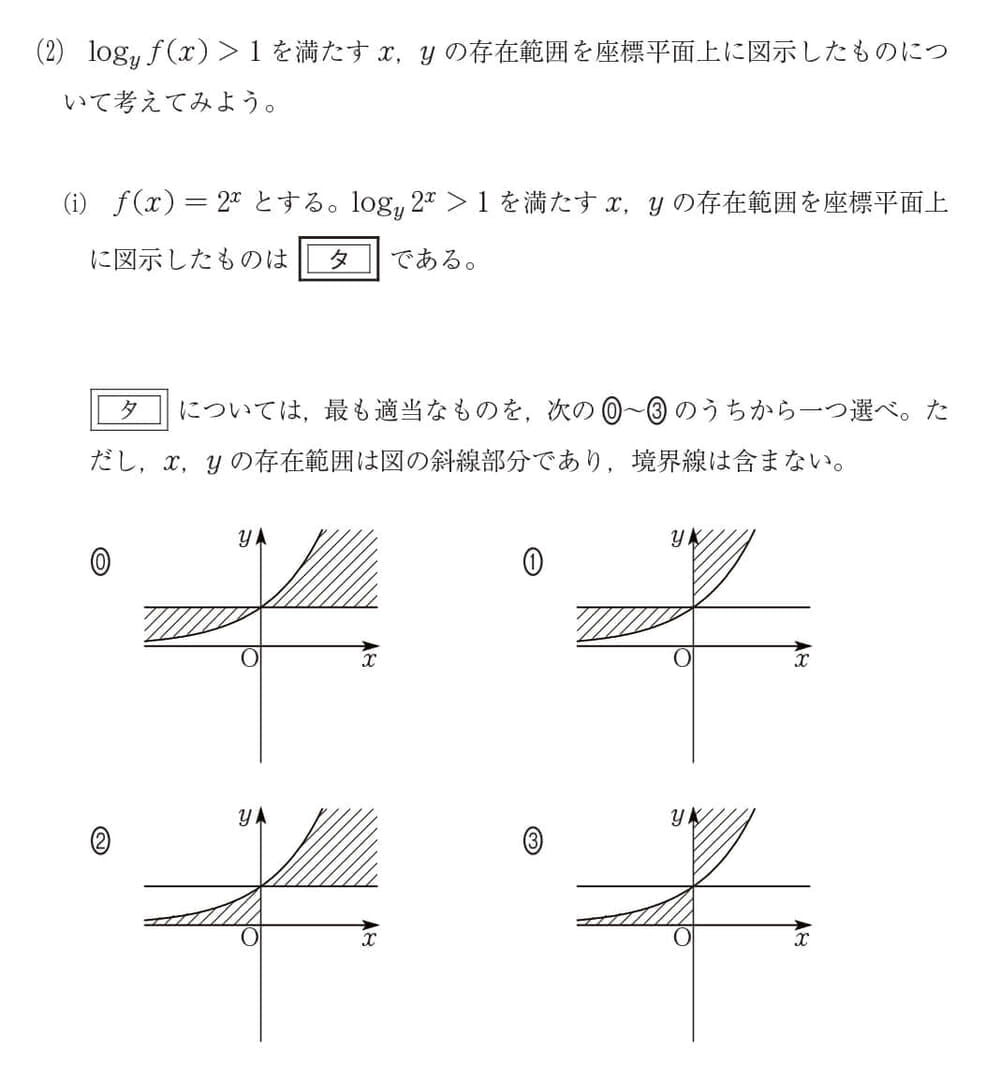
図２

このような結果から、2025年度用の教材も同様の方針で作成を進めています。

裏話として、2025年度の教材で使用する問題は、新課程ということもあり、共通テスト実施前に作成を始めたのですが、2024年度の追試と同内容の問題となってしまい、使用することを諦めた問題もありました。

新課程入試の問題は？

新課程での問題はまだありません。そんな中、どのような分析を進めたかというと、令和4年11月に大学入試センターから発表された試作問題を参考にしました。

https://www.dnc.ac.jp/kyotsu/shiken_jouhou/r7/r7_kentoujoukyou/r7mondai.html

試作問題の内容は次の通りです。いずれも、2021年度本試験第一日程をベースに作られています。

【数学ＩＡ】

第１問〔１〕数と式　　〔２〕図形と計量
第２問〔１〕二次関数　〔２〕データの分析
第３問　図形の性質
第４問　場合の数と確率

旧課程の内容からは「整数の性質」の問題がなくなり、全問必答となりました。これまで「図形の性質」が最後の問題でしたが、「場合の数と確率」の問題よりも先になりました。
新課程対応問題として、新たに作成されたのは「データの分析」と「場合の数と確率」の問題です。ほかの分野の問題は何も変えていないことをふまえると、全体のボリュームや難易度は大きく変わらないだろうと予想しています。

【数学ＩＩＢＣ】

第１問　三角関数
第２問　いろいろな式、指数関数・対数関数
第３問　微分・積分の考え
第４問　数列
第５問　統計的な推測
第６問　ベクトル
第７問〔１〕平面上の曲線　〔２〕複素数平面

旧課程の構成と大きく異なり、第１問が中問構成であったのが、大問構成になりました。流用元がそのまま利用されており、配点も変わらないので、「三角関数」、「いろいろな式」、「指数関数・対数関数」は、これまでのボリュームや難易度での出題と予想しています。
第３問の「微分・積分の考え」は、これまで30点の配点でしたが、22点になり、流用元の問題もいくつか省かれていたので、ボリュームは減ると思いますが、最後の設問が残っていることを考えると、難易度としては、これまでと変わらないのではと予想しています。ここまでが数学ＩＩで、全分野必答であることは変わりません。
大きく変わるのが第４問以降の数学Ｂ、Ｃです。これまでは３分野から２分野選択だったのが、４分野から３分野選択に変わります。出題順も変わりました。配点も20点から16点となりました。
「数列」と「ベクトル」は、「微分・積分の考え」と同様、流用元の問題から、いくつか設問が省かれているものの最後の設問は残っていました。こちらもボリュームは減るが、難易度としては、これまでと変わらないと予想しています。
「統計的な推測」と「平面上の曲線と複素数平面」は、新課程対応問題として新たに作成されました。
「統計的な推測」については、新課程で仮説検定が入り、この内容の問題も出題されました。「平面上の曲線と複素数平面」については、中問２題構成で、設問１つ４点の「平面上の曲線」と設問５つで配点12点の「複素数平面」という構成でした。

数学ＩＩＢＣの方は、70分に試験時間は増えますが、センター試験の数学ＩＩＢのときと同様に、試験時間が足りないボリュームや難易度になると予想しています。

新課程入試対策の問題をどう作るか

共通テスト対策模試を実施していない弊社の場合、前年度の教材をベースに次年度の教材を検討します。2025年用については、試作問題を元にどのような問題を加えるのか、構成をどうするか検討し、制作を進めることにしました。

【数学ＩＡ】

大問構成は試作問題と同じ。ただし、第１問については、中問２題構成と３題構成が混在していることをふまえ、両方のパターンを準備することにしました。
試作問題において、新規で作成されなかった分野については、これまでの出題とあまり変わらないという予想で編集することにしました。
「データの分析」については、外れ値や仮説検定の考え方といった内容が加わり、試作問題では、この２つの内容も含まれていました。これまで、この分野で頻出内容であった箱ひげ図や四分位範囲については、今回の課程で中学の履修範囲となりました。実際、試作問題を見ると、箱ひげ図や四分位範囲の問題は入っていますが、いずれも外れ値を含んだものであり、中学履修内容だけの問題は出題されていないことをふまえ、すべての問題を数学Ｉで履修する内容で構成された問題としました。
「場合の数と確率」については、期待値の内容が新たに加わりました。旧課程で出題された内容は、共通テストの作成方針をふまえており、今後も出題されると想定しています。一方、作成方針の中にある「社会や⽇常の中から課題を発⾒し解決⽅法を構想する場⾯」は、期待値の内容が当てはめやすいことや、過去問では学習できないことから、期待値の内容を扱う問題を多めに準備することにしました。

【数学ＩＩＢＣ】

大問構成は試作問題と同じ。ただし、数学ＩＩの「三角関数」、「指数関数・対数関数」、「図形と方程式」については、どの分野が出てもよいように、色々な組み合わせのものを準備しました。
また、試作問題の配点とするため、既存の分野については、難易度と分量調整を行い、問題を編集することにしました。
「平面上の曲線と複素数平面」については、試作問題と同じようなタイプの問題も準備しましたが、過去の試作問題と本番の形式の違いを考えると、同じような出題になる可能性の方が低いのではと考え、「平面上の曲線」だけの問題、「複素数平面」だけの問題、中問２題構成でも「平面上の曲線」の割合が多い問題など、複数のパターンを準備し、どのようなパターンが出ても対応できるようなセットを準備することにしました。
「統計的な推測」については、仮説検定の内容が新たに加わりました。こちらも「場合の数と確率」と同様に、旧課程で出題された内容は、今後も出題されると想定していますが、過去問では学習できないことから、仮説検定の内容を扱う問題も複数準備することにしました。

なお、選択する受験生が増えると思われる「統計的な推測」については、共通テストレベルの到達を目標とした学校用書籍を準備しております。これまで共通テストで出題された「統計的な推測」の解答解説も提供しておりますので、短期間で対策をしたいときは、こちらの書籍をご利用いただくこともお勧めします。

新課程共通テストの予想をふまえたＺ会書籍の強み、効果的な使い方

新課程初年度の対策としては、既存範囲の問題の分量や難易度設定は、過去問がいちばん把握しやすいと思いますので、過去問での対策がお勧めです。
弊社から出版している『2025年用共通テスト実戦模試』には過去問も掲載しております。英数国の過去問をまとめた『2025年用共通テスト過去問　英数国』もあります。これらを利用して対策できます。

新課程から入ってきた問題は、過去問にないので、オリジナル問題での対策がお勧めです。
新課程のオリジナル問題が多い教材で対策するのがよいでしょう。弊社書籍の『2025年用　パワーマックス』や『2025年用共通テスト実戦模試』は「大学入学共通テスト問題作成方針」に合致し、出題が予想される内容を幅広く扱い、入試当日に、どこかで経験したことのある問題になるように準備しています。

また、2025年用教材の解答解説は、解説を読むのは、解けない問題のところだけだろうという判断から、形式をこれまでと変え、解くのが厳しい人に理解しやすい内容となるよう、レイアウトや内容をこれまでと一新しました。

目標の点数を目指す人がその目標点のレベルで学習しても、本番当日、その点数に到達するのは難しいと考えます。普段から、目標よりも少し上を目指した学習をすることで、目標の点数に近づくと考えます。
Ｚ会の書籍は難しいという話を聞きます。難しく作っているわけではないのですが、結果として、本番より難しいもので訓練することで、当日、高得点を取ることができるという点で、適切な教材ではないでしょうか。

また、弊社書籍の利用の仕方として、目標の点数が高い人は、パワーマックスや実戦模試を最初の1冊として学習を始め、最後に予想問題や模擬試験で完成させる。
目標の点数が平均点くらいの人は、過去問や『共通テスト分野別演習』、『ハイスコア！共通テスト攻略』などの問題集から始めて、それが終わった後にパワーマックスや実戦模試を利用いただき、最後に予想問題や模擬試験で完成させる。
まだ制限時間内では解けないような段階では、解答時間を気にせず解き、問題の考え方などを身につけるのに利用するなど、利用する方の目標やレベルに合わせて、いろいろな使い方ができます。

本番当日に十分な力を発揮することができるようにするために、これまでの共通テストを分析して、出題予想をして作成した弊社書籍で、新課程入試初年度を乗り切れることを願っております。

共通テスト数学 新課程入試に向けて ～試作問題の分析結果、新課程共通テストの出題予想～

問題をどう作っているのか

新課程入試の問題は？

【数学ＩＡ】

【数学ＩＩＢＣ】

新課程入試対策の問題をどう作るか

【数学ＩＡ】

【数学ＩＩＢＣ】

新課程共通テストの予想をふまえたＺ会書籍の強み、効果的な使い方

共通テスト数学　新課程入試に向けて　～試作問題の分析結果、新課程共通テストの出題予想～