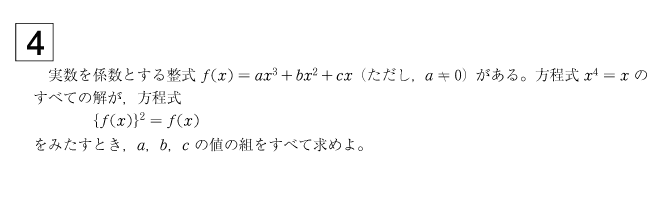※入会フォームでは「数学」をお選びください。文系/理系は入会後にご選択いただきます。
※数IIIを必要としない理系の方は「文系数学」をご覧ください。


“実戦力向上サイクル”で
理系数学で差をつける

演習経験が勝負を分ける理系数学。Z会なら、難関大入試で問われる力を体系化し反映した良問で、年間通じて質の高い演習をおこなうことができます。前半期は、入試レベルの問題に対応するための基盤を固め、後半期は志望大の傾向にあわせた演習で、あらゆる分野に対応できる横断的思考力と論理的記述力を強化できます。


こんなお悩み、
「着眼点アシスト」が
解決します!

問題を解くうえで鍵となるポイントを提示。つまずいたときに、その場で着眼点を確認できるため、最後まで考え抜く経験ができ、理解が深まります。
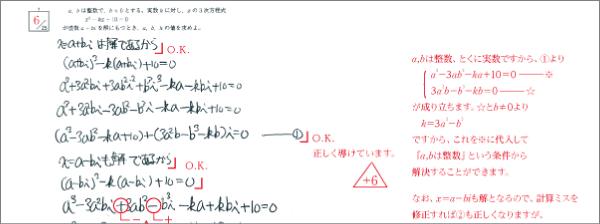
数学専門のプロの添削者があなたの答案を添削。数多くの答案を見てきた経験から、あなたの解答の意図を読み取り、得点力を伸ばすための的確な指導を行います。添削指導と解答解説による復習で、知識や解法が完全に定着します。
近年の数学の入試では、受験生が経験のない問題を出題し、知識を組み合わせて解決する力が重視されています。そこでZ会の理系数学では、試行錯誤する機会を増やす工夫をしています。考える問題の出題はもちろんのこと、解答解説ではさまざまな解法を紹介しています。そして、懸命に問題を考え、その成果を答案としてまとめてもらい、添削指導で丁寧に振り返ることで、入試に直結する解決力を養っていきます。
飯田 健一

志望大にあわせて
無理なく伸びる学習設計
志望大別に5つの講座をご用意。入試で重視される力は大学ごとに違うから、
必要な力を効率的に身につけられるよう、志望大別に学習設計を最適化しました。
東大講座
1年間の学習体系
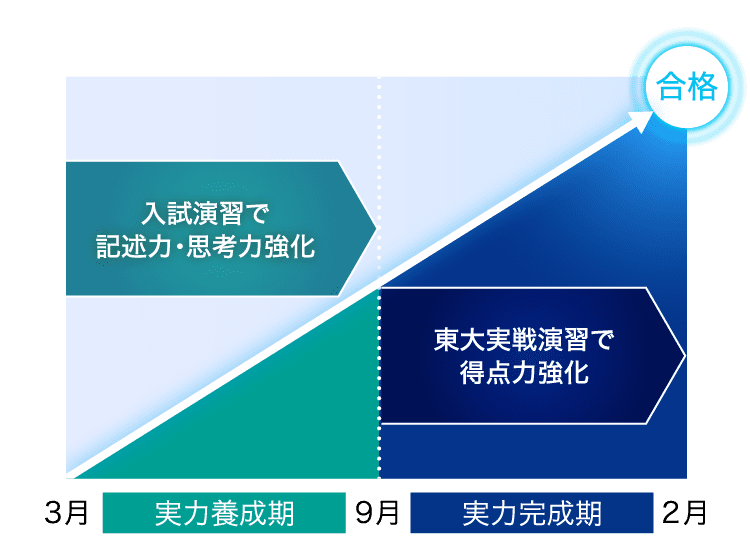
東大数学講座のポイント
※「SEG」「科学的教育グループSEG」は、株式会社エスイージーの登録商標です。
カリキュラム(入試演習)
| 1回目 | 2回目 | 3回目 | 4回目 | |
| 3月 | 数式処理と論理1 | 総合問題1 | 数式処理と論理2 | 総合問題2 |
| 4月 | 確率1 | 総合問題3 | 確率2 | 総合問題4 |
| 5月 | 図形問題1 | 総合問題5 | 図形問題2 | 総合問題6 |
| 6月 | 図形問題3 | 総合問題7 | 数列と論証 | 総合問題8 |
| 7月 | 整数問題1 | 総合問題9 | 整数問題2 | 総合問題10 |
| 8月 | 理系数学の重要事項1 | 総合問題11 | 理系数学の重要事項2 | 総合問題12 |
※9月以降の実力完成期は毎月2回、東大実戦演習に取り組みます。
教材見本
学習時間目安
3~8月:60分×月4回
9~12月:120分×月2回
1~2月:入試に即した時間×月2回
学習ツール
3〜8月:紙の教材+タブレット
9〜2月:紙の教材+タブレット
京大講座
1年間の学習体系

京大数学講座のポイント
※「SEG」「科学的教育グループSEG」は、株式会社エスイージーの登録商標です。
カリキュラム(入試演習)
| 1回目 | 2回目 | 3回目 | 4回目 | |
| 3月 | 数式処理と論理1 | 総合問題1 | 数式処理と論理2 | 総合問題2 |
| 4月 | 確率1 | 総合問題3 | 確率2 | 総合問題4 |
| 5月 | 図形問題1 | 総合問題5 | 図形問題2 | 総合問題6 |
| 6月 | 図形問題3 | 総合問題7 | 数列と論証 | 総合問題8 |
| 7月 | 整数問題1 | 総合問題9 | 整数問題2 | 総合問題10 |
| 8月 | 理系数学の重要事項1 | 総合問題11 | 理系数学の重要事項2 | 総合問題12 |
※9月以降の実力完成期は毎月2回、京大実戦演習に取り組みます。
教材見本
学習時間目安
3~8月:60分×月4回
9~12月:120分×月2回
1~2月:入試に即した時間×月2回
学習ツール
3〜8月:紙の教材+タブレット
9〜2月:紙の教材+タブレット
最難関講座
1年間の学習体系

最難関数学講座のポイント
カリキュラム(入試演習)
| 1回目 | 2回目 | 3回目 | 4回目 | |
| 3月 | 2次関数/式と証明 | 三角関数/指数・対数関数 | 数式処理と論理1 | 数式処理と論理2 |
| 4月 | 場合の数と確率 | 図形と計量/図形の性質 | 確率1 | 確率2 |
| 5月 | 図形と方程式 | ベクトル | 図形問題1 | 図形問題2 |
| 6月 | 数列 | 微積分(数学Ⅱ) | 図形問題3 | 数列と論証 |
| 7月 | 整数 | 総合問題1 関数編 | 整数問題1 | 整数問題2 |
| 8月 | 総合問題2 図形編 | 総合問題3 確率・数列編 | 理系数学の重要事項1 | 理系数学の重要事項2 |
※9月以降の実力完成期は毎月2回、最難関大実戦演習に取り組みます。
教材見本
学習時間目安
3~8月:60分×月4回
9〜2月:120分×月2回
学習ツール
3〜8月:タブレット
9〜2月:紙の教材+タブレット
早慶大講座
1年間の学習体系

早慶大数学講座のポイント
カリキュラム(入試演習)
| 1回目 | 2回目 | 3回目 | 4回目 | |
| 3月 | 2次関数/式と証明 | 2次関数/式と証明 | 三角関数/指数・対数関数 | 三角関数/指数・対数関数 |
| 4月 | 場合の数と確率 | 場合の数と確率 | 図形と計量/図形の性質 | 図形と計量/図形の性質 |
| 5月 | 図形と方程式 | 図形と方程式 | ベクトル | ベクトル |
| 6月 | 数列 | 数列 | 微積分(数学Ⅱ) | 微積分(数学Ⅱ) |
| 7月 | 整数 | 整数 | 総合問題1 関数編 | 総合問題1 関数編 |
| 8月 | 総合問題2 図形編 | 総合問題2 図形編 | 総合問題3 確率・数列編 | 総合問題3 確率・数列編 |
※9月以降の実力完成期は毎月2回、早慶大実戦演習に取り組みます。
教材見本
学習時間目安
3〜8月:60分×月4回
9〜2月:120分×月2回
学習ツール
3〜8月:タブレット
9〜2月:タブレット
難関講座
1年間の学習体系

難関数学講座のポイント
カリキュラム(入試演習)
| 1回目 | 2回目 | 3回目 | 4回目 | |
| 3月 | 2次関数/式と証明 | 2次関数/式と証明 | 三角関数/指数・対数関数 | 三角関数/指数・対数関数 |
| 4月 | 場合の数と確率 | 場合の数と確率 | 図形と計量/図形の性質 | 図形と計量/図形の性質 |
| 5月 | 図形と方程式 | 図形と方程式 | ベクトル | ベクトル |
| 6月 | 数列 | 数列 | 微積分(数学Ⅱ) | 微積分(数学Ⅱ) |
| 7月 | 整数 | 整数 | 総合問題1 関数編 | 総合問題1 関数編 |
| 8月 | 総合問題2 図形編 | 総合問題2 図形編 | 総合問題3 確率・数列編 | 総合問題3 確率・数列編 |
※9月以降の実力完成期は毎月2回、難関大実戦演習に取り組みます。
教材見本
学習時間目安
3〜8月:60分×月4回
9〜2月:120分×月2回
学習ツール
3〜8月:タブレット
9〜2月:タブレット

東京工業大学 理学院合格
N.T.さん
Z会の数学では、見たことのない解法も紹介されていたので、自分でも使えるように吸収していきました。また、添削指導では、記述答案に盛り込むべき要素や、論理展開の仕方を学ぶことができました。解答解説に載っていない解法で解いても、その解き方に応じた採点やアドバイスをしてもらえたので、正しい解き方を定着させることができました。
※入会フォームでは「数学」をお選びください。文系/理系は入会後にご選択いただきます。
※数IIIを必要としない理系の方は「文系数学」をご覧ください。
個別の課題解決は
タブレットでより効果的に
2025年度から大学受験コースはタブレットを中心とした学習に進化。
紙教材と同様の「書くことにこだわる」学習を行いながら、
紙教材では実現できない個別最適な学習も提供します。
3月〜8月は学校にあわせて知識の補強を
単元別強化学習
学習時期が遅くなりがちな理系数学の範囲について、基礎からの学習により理解を深められます。
映像授業と演習を通じて難関大入試レベルに必要な基盤を固めます。


1カ月あたりの学習量は30分×8回。
スキマ時間を使って、基礎知識を固められます。
| 3月 | 平面上の曲線 |
|---|---|
| 4月 | 複素数平面 |
| 5月 | 極限 |
| 6月 | 微分法 |
| 7月 | 微分法/積分法 |
| 8月 | 積分法 |
さらにデジタルで進化!

標準カリキュラムに加え、高校範囲の全単元をいつでも自由に学習可能。
自分の状況にあわせて活用できます。

ヌケモレの確認や演習の強化に
プラス演習
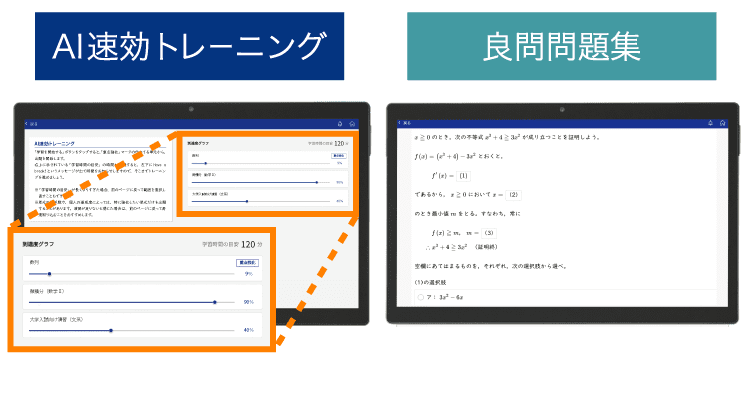
自動判定
入試レベルまで
難易度別演習
「AI速効トレーニング」では、AIが単元ごとに到達度を判定。到達度の低い単元から固めることで、解法や公式のヌケモレをなくすことができます。
「良問問題集」は、単元別・難易度別に取り組み可能。基礎レベルの知識の確認から入試に近い発展的な問題演習まで行えます。
※入会フォームでは「数学」をお選びください。文系/理系は入会後にご選択いただきます。
※数IIIを必要としない理系の方は「文系数学」をご覧ください。
受講会費・受講環境
受講会費
オールインワンで取り組める!